MeshFree|第三代轮毂轴承旋转弯曲疲劳分析
摘要随着汽车制造业的换代升级,对轮毂轴承单元提出了长寿命、轻量化、高集成度等更高要求。这些都是对轮毂轴承性能,尤其是寿命的高要求,以期改善汽车行驶的稳定性和安全性。本文的研究对象是三代轮毂轴承,主要研究内容如下:对汽车轮胎进行受力分析,合理制定出两种状态下的载荷谱。对轴承轴向载荷和径向载荷进行分析,依据 ISO16281 修正 Lundberg-Palmgren 公式,求得额定动载荷,计算出两种状态下的轮毂轴承的理论寿命。建立三维模型,并适当简化。用无网格划分软件 MeshFree,进行静力学分析,初步得到形变量和应变位置。在 ABAQUS 的动力学模块中对有限元模型进行了材料参数、边界条件、网格划分等设置,得到了不同状态下轮毂轴承的应力应变云图。结果表明,最大接触应力位于滚动体与内外圈接触处。用 nCode 模拟出材料的 S-N 曲线,同时将载荷谱和有限元结果输入 nCode。对轴承进行疲劳寿命预测,得到不同状态下轮毂轴承寿命和损伤云图,即数值仿真的轮毂轴承疲劳寿命。使用旋转弯曲疲劳试验机,按照所设计的试验方法,设置参数,进行实验,得到试验结果,与轮毂轴承数值仿真的寿命进行对比分析,试验结果与仿真结果误差为8.765%。验证了数值仿真模型的可行性。对试验结果进一步处理,先拟合,再进行可靠性评估,得到两种状态下的可靠性函数图,评估预测结果的可靠度。用 SVM 模型进行寿命预测,得到轴承失效预测准确度,因试验数据较少,故准确度较低为 75%,这是模型优化的初步探索。通过分析,目前国内大部分在轮毂轴承疲劳寿命和试验技术的研究方面仍存在一定差距,轴承的耐受性不佳导致其使用寿命表现不佳会对汽车的使用寿命造成直接影响,也是汽车暴露出安全问题的一大重要原因。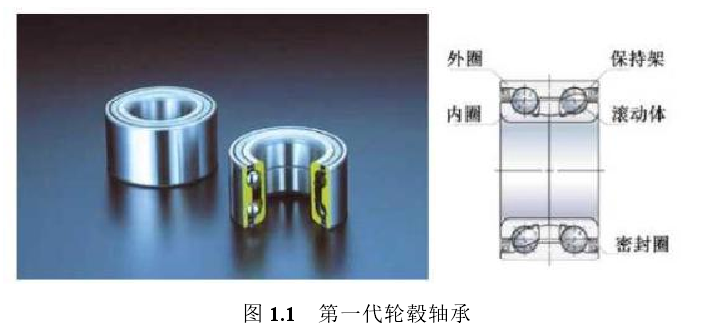

第三代轮毂轴凭借一体化结构与第一代相比,重量降低了 20%。疲劳是一种机械损伤过程。一般由长时间运作等原因导致的疲劳,而后表现出零部件的损坏或者失效。根据中国机械工程手册第 6 章给出的标准,机械零部件如果损伤程度超过 80%,就可以认定为疲劳破坏。因而,对零部件疲劳寿命的研究至关重要。从传统解决疲劳问题来讲,工程中采用的策略为先将产品设计好,然后交给用户使用(或者采用加速的产品考核试验),通过用户使用后反馈产品寿命信息重新进行设计,最后再次给用户使用,依次反复循环,这样耗时耗力也得不到精确的结果。现在采用的是一体化解决疲劳耐久性策略,就是采用计算机辅助疲劳寿命模拟得到产品寿命,将计算机模拟得到的寿命与加速试验得到的零部件寿命进行关联,这样在今后进行同种类型的产品设计时就提供了数据参考,仅需计算机模拟得到零部件的寿命,无需做试验,这样不仅缩短了产品设计的时间,也降低了成本。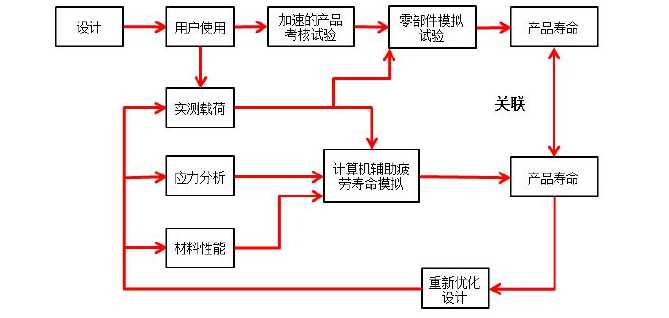
本文是对三代轮毂轴承的疲劳寿命进行预测,首先,对汽车轮胎进行受力分析,制定两种状态下的载荷谱。然后,对轴承所受载荷进行分析,根据 L-P 理论,计算得到理论寿命。建立轮毂轴承三维模型并简化,用 MeshFree 中进行无网格划分的静力学分析,使用 ABAQUS 软件完成对轮毂轴承的动力学分析。将上述有限元分析的结果、S-N 曲线和载荷谱,借助 nCode 软件进行下一步的疲劳寿命计算工作。最后,用旋转弯曲疲劳试验机进行试验,对试验结果分析处理,以验证寿命模型的可行性。对数据进一步处理,进行可靠性分析和寿命预测,探索模型的优化。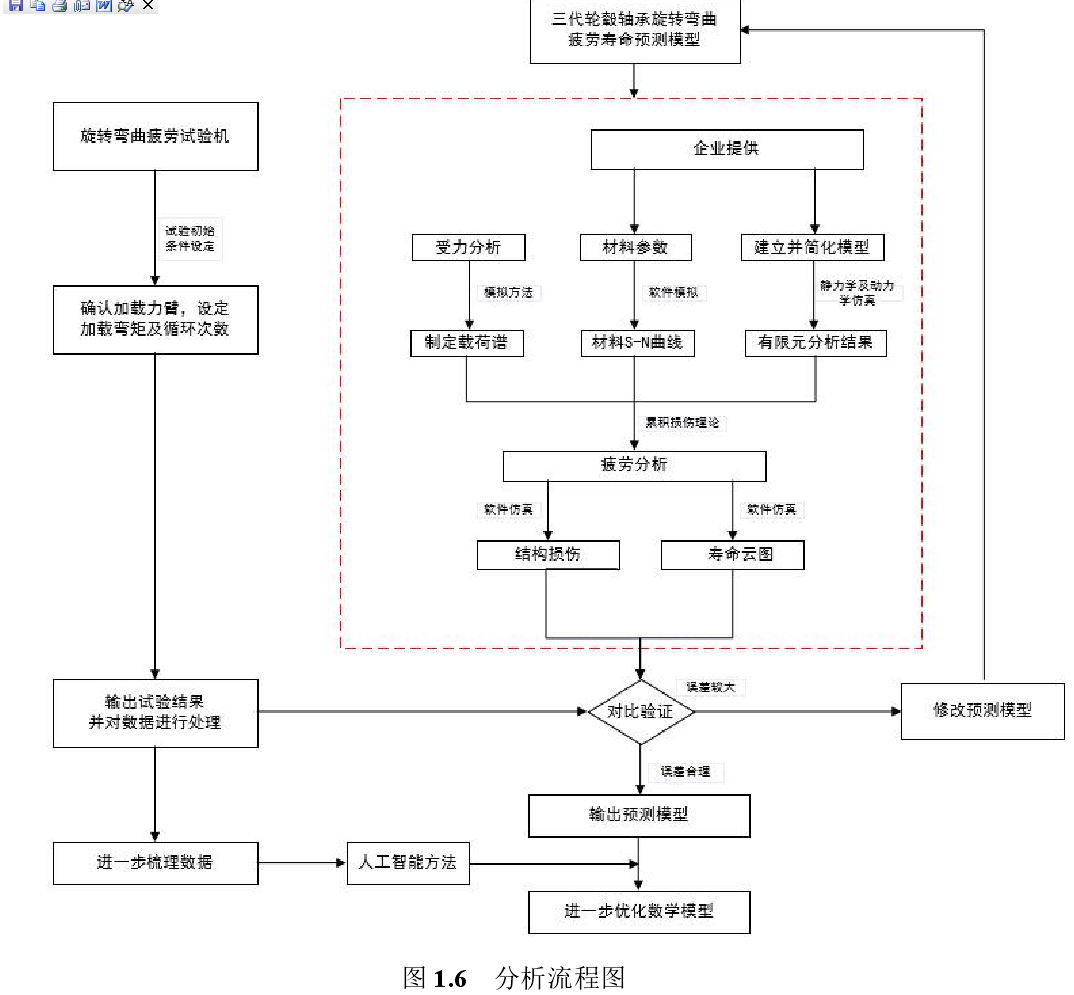
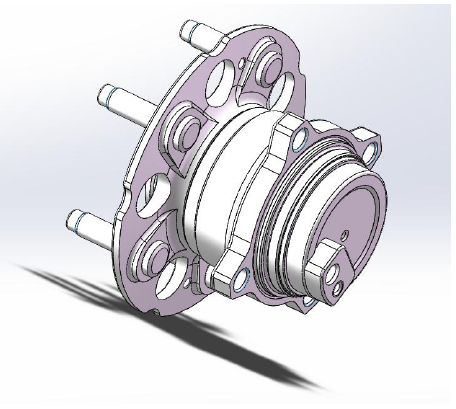
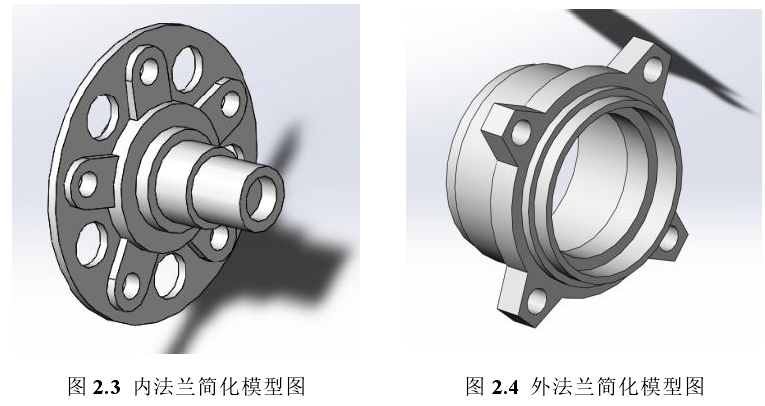
轮毂轴承载荷谱制定与寿命计算。在 SolidWorks 中创建了轮毂轴承的三维模型并简化。参考其他公司的经验,对不同加速度下的轮毂轴承进行受力分析,制定出轴承在两种状态下的载荷谱。依据 L-P 理论,计算出 0.6g 和 0.8g 状态下轮毂轴承的理论寿命。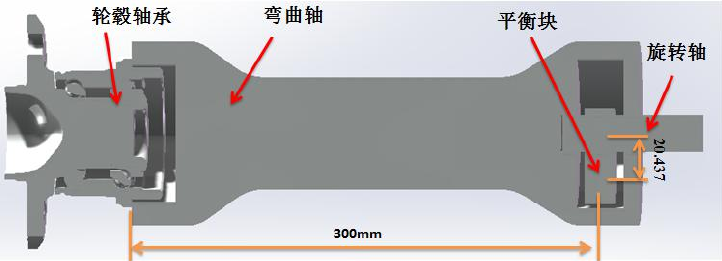


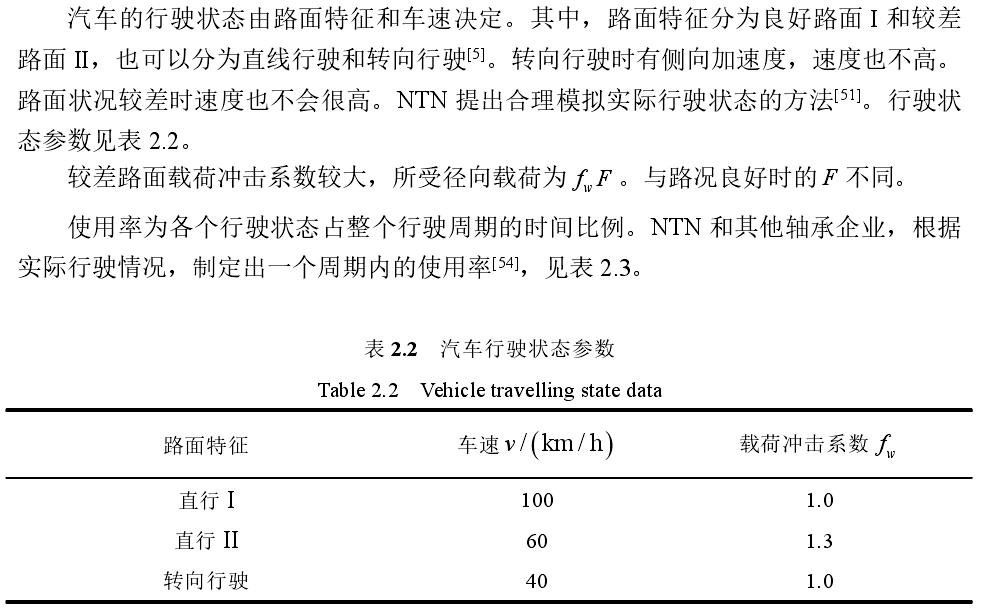
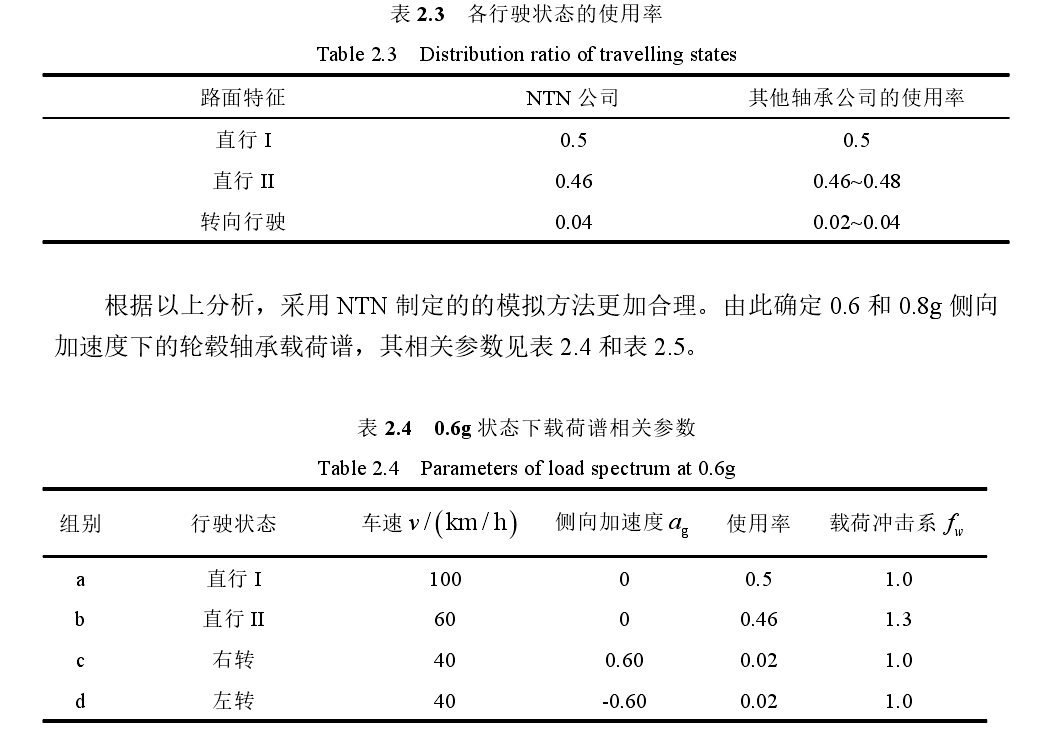
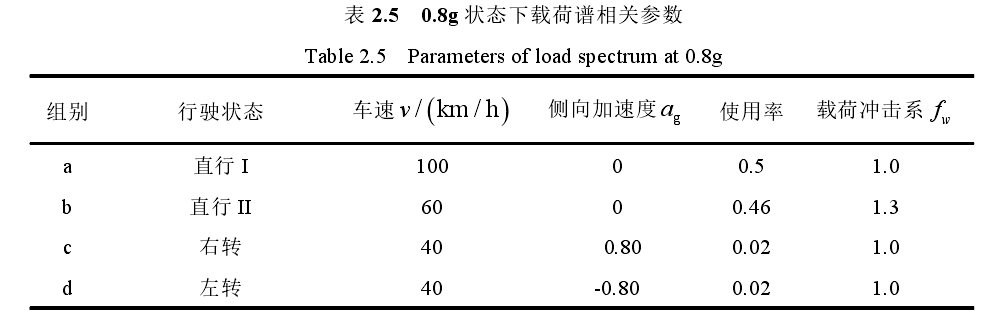
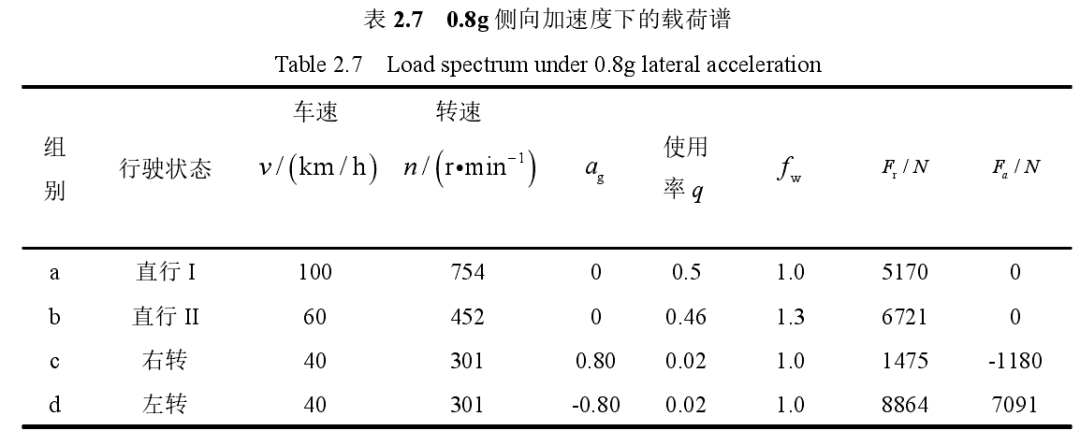
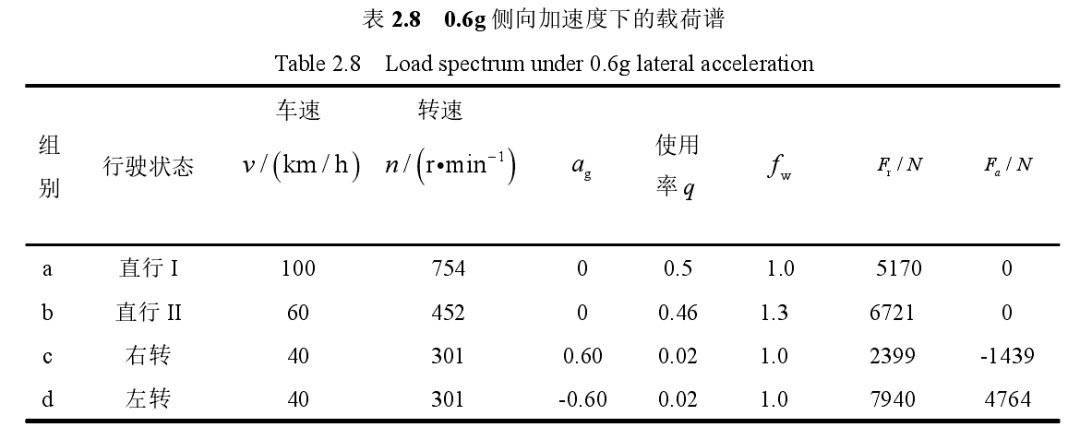
轮胎载荷计算汽车行驶过程中路面对轮胎的反作用力,即为轮胎载荷[6]。根据力的传递特性,可近似认为轮胎载荷等价于轮毂轴承外载荷。轮胎载荷通常可分为径向和轴向。因此轮毂轴承径向和轴向外载荷计算公式如下式 (2-1)~(2-4),式(2-1)(2-2)适用于前轴或后轴的右轮,式(2-3)(2-4)适用于前轴或后轴的左轮。 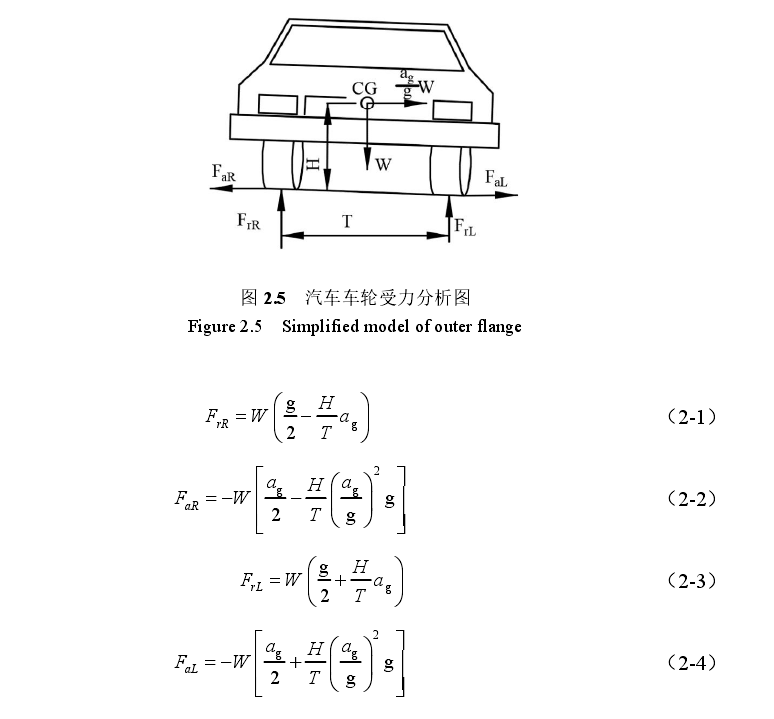

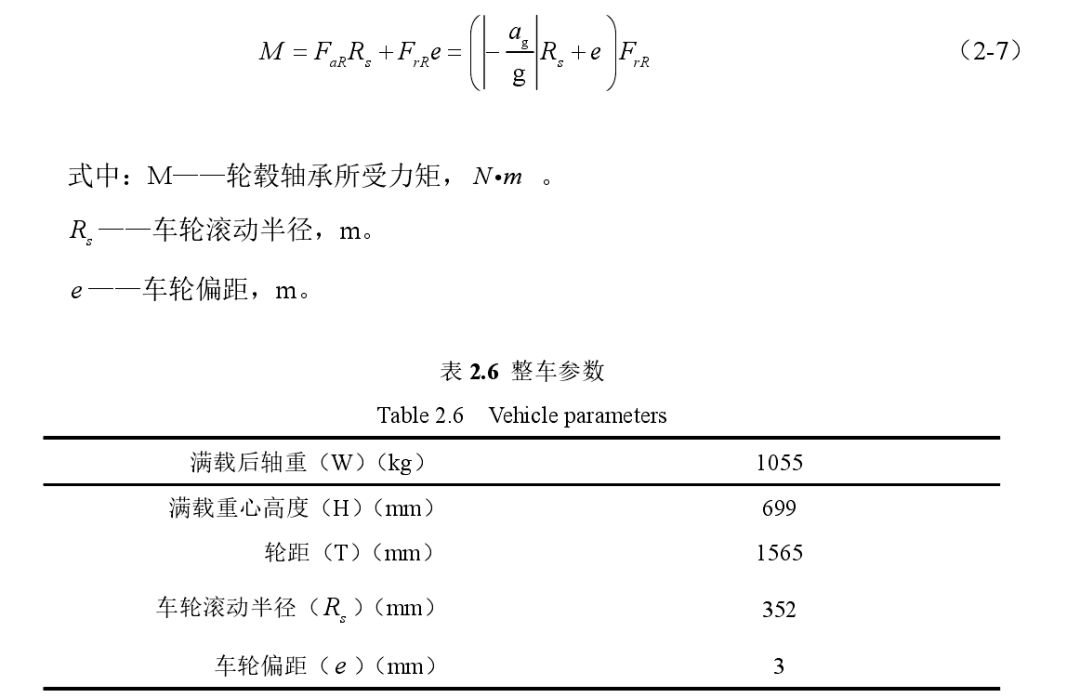
表2.6 给出了进行载荷计算所需的某型号汽车的整车参数,以后轴右轮为例,将整车参数代入式(2-1)(2-2)和(2-7),得到结果如下表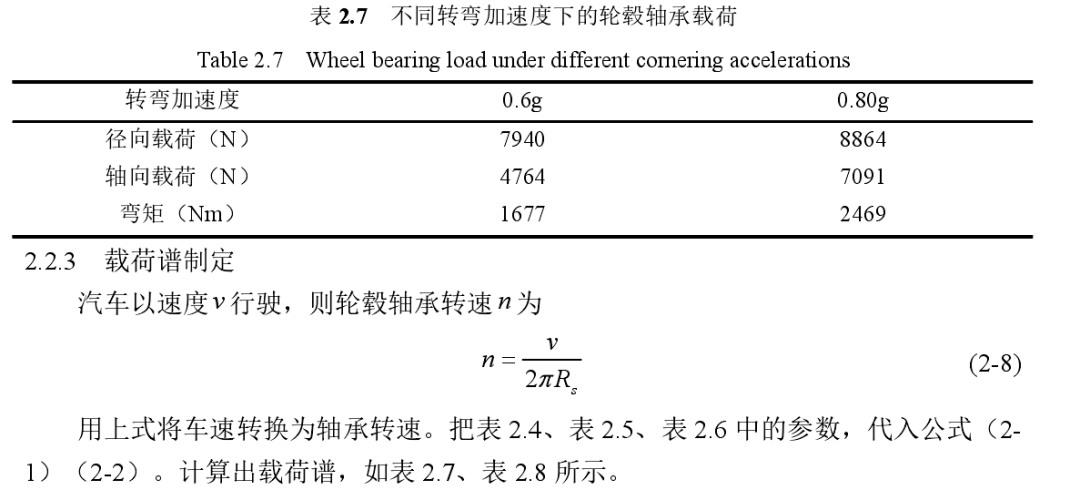
静力学中常用是赫兹接触理论,轮毂轴承接触属于线接触,有限元分析过程为:建立模型——求解——后处理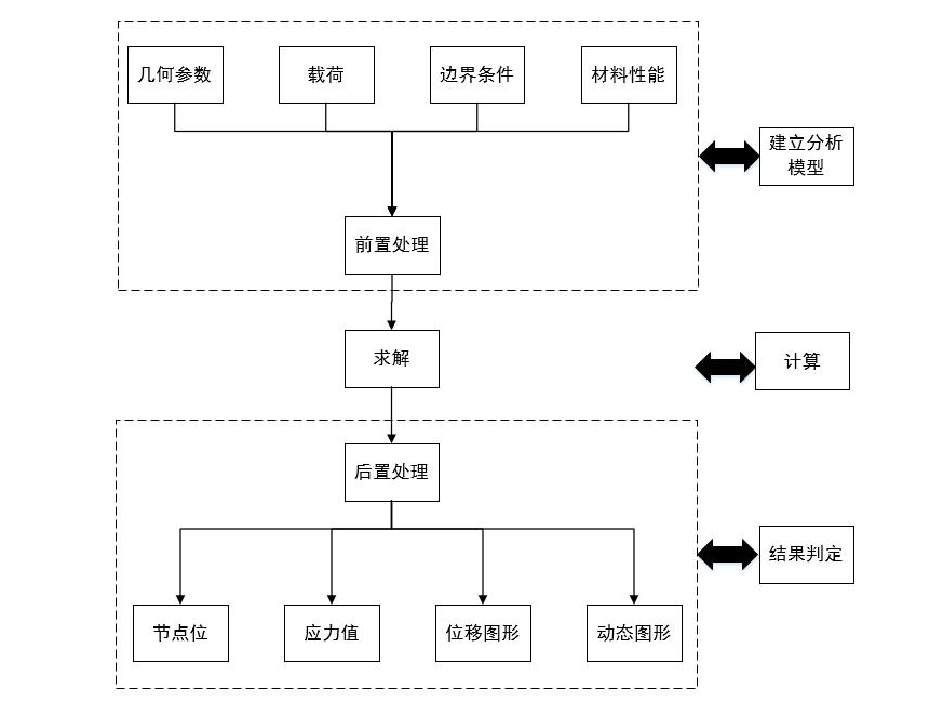
MeshFree 无网格划分算法基本上是一种求物理问题近似解的方法,它将模型划分为若干个由节点相连接的单元组成,并找到物理问题的近似解。采用隐式边界法(IBM),独立于分析模型的结构化网格。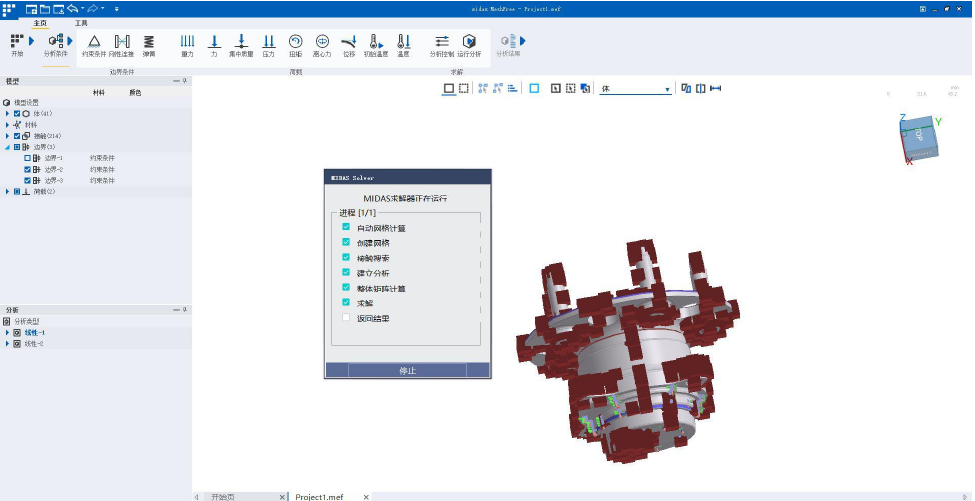
建材料属性——赋予零件——建立接触对——设置边界约束条件——静力学求解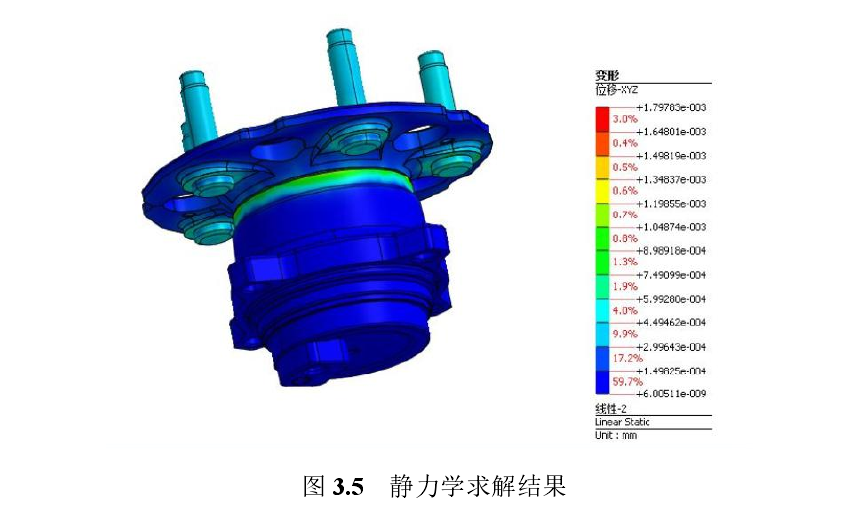
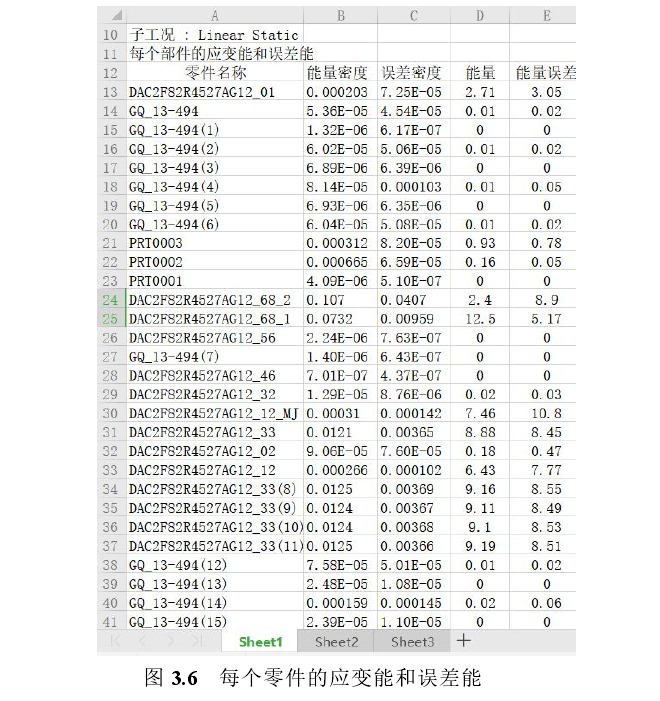
最大变形为 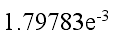 ,发生在滚子周围。导出分析结果及误差,得到应变能和误差能表格
,发生在滚子周围。导出分析结果及误差,得到应变能和误差能表格
以三代轮毂轴承为研究对象,在参考其他轴承公司的经验与实例的基础上,对轴承进行受力分析,制定了载荷谱,依据 Lundberg-Palmgren 寿命理论,计算出 0.6g 和 0.8g 状态下轮毂轴承的理论寿命。利用 SolidWorks创建了轮毂轴承的三维模型,并对其进行简化。然后使用有限元软件 MeshFree 中进行无网格划分的静力学分析,ABAQUS 进行动力学分析。其次,使用疲劳寿命预测软件nCode DesignLife 对轴承进行了疲劳寿命分析。然后,通过旋转弯曲疲劳试验机进行试验,处理试验结果,对比验证了预测结果。最后,对试验结果进一步处理,进行了可靠性评估,同时,用 SVM 进行了失效预测,以探索模型优化。利用 SolidWorks 软件创建了三代轮毂轴承的三维模型,根据有限元仿真的需要,简化不必要的特征,得到简化模型。根据理论计算的工况及试验工况在 MeshFree中进行无网格划分的静力学分析,得到最大形变量和应变位置。在 ABAQUS 的动力学模块中对有限元模型进行了材料参数、边界条件、网格划分等设置,得到了轮毂轴承的应力应变云图,结果表明,轮毂轴承最大接触应力存在于滚子与内外圈接触处。
因篇幅有限,本文摘自“刘思源《三代轮毂轴承旋转弯曲疲劳仿真及试验研究》”专业学位硕士学位论文中的内容,如有感兴趣的可联系作者本人。
本文来源于网络,如有侵权请联系删除!





















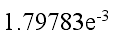 ,发生在滚子周围。导出分析结果及误差,得到应变能和误差能表格
,发生在滚子周围。导出分析结果及误差,得到应变能和误差能表格




