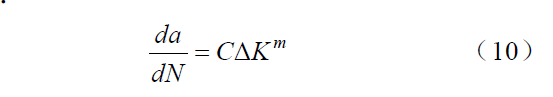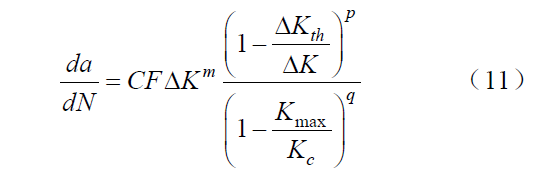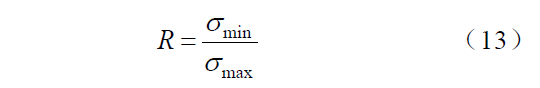NFX|疲劳分析应用
基于MIDAS NFX和AFGROW的既损构件疲劳寿命分析(中国建筑第七工程局有限公司,郑州 450000)
[摘要] 断裂力学广泛应用于航空航天、核、造船、汽车制造、结构工程等领域。本文利用MIDAS NFX和AFGROW分析了有缺口的构件。在MIDAS NFX中,通过不同的疲劳荷载函数可以获得缺口构件的疲劳寿命,在组装后可以得到近似的S-N 函数。本文采用了MIDAS NFX 对缺口构件进行分析,然后在AFGROW 中定义了相同的荷载和材料特性。将MIDAS NFX 归一化应力导入AFGROW 当中,从而预测裂纹扩展寿命。[关键词] 断裂力学;疲劳寿命;有限元分析;数值法分析中图分类号:TU313 文献标识码:A 文章编号:1002-848X(2021)S1-1528-04Fatigue life analysis of damaged components based on MIDAS NFX and AFGROWGUO Wenbo, JIE Shiqin, GUO Yuanxin, ZHU Lei(China Construction Seventh Engineering Division. Co., Ltd., Zhengzhou 450000, China)Abstract: Fracture mechanics is widely used in aerospace, nuclear, shipbuilding, vehicle manufacturing, structural engineering and other fields. In this paper, Midas NFX and AFGROW are used to analyze notched specimens. In MidasNFX, the fatigue life of notched specimens can be obtained by different fatigue load functions, and the approximate S-N function can be obtained after assembling. In the two software, through the analysis of Midas NFX notch samples, the same load and material characteristics are defined in AFGROW. Then the normalized stress is introduced into the stress intensity coefficient column of AFGROW to predict the crack propagation life.Keywords: fracture mechanics; fatigue life; finite element method; numeric method断裂力学已广泛应用于航空航天、核、造船、车辆制造和结构工程。直到第二次世界大战之前,科学家和工程师们对断裂力学的研究都是有限的。在第二次世界大战期间,美国军队建造了2700多艘自由船,其中1031 艘因断裂而受损。超过200 艘船沉没或损坏[1]以致无法修复。调查组对故障的调查得出结论,发现大部分裂纹始于甲板门的四个角,那里存在应力集中现象。对美国自由船断裂失效的研究可以看作是断裂力学的诞生。格里菲斯教授在20 世纪20 年代发表的著作一种模拟脆性材料断裂的表面能方法被认为在断裂力学领域具有里程碑[2]象征。50 年代,欧文教授发现格里菲斯的研究主要适用于玻璃等脆碎材料。对于金属等韧性材料,欧文引入了对应力强度因子(SIF)[3]的概念,来解决钢等韧性材料的断裂。这两种理论为断裂力学奠定了基础。近年来,有人提出了额外的方法和模型,以解决更为复杂的问题的方法。该方法基于裂纹扩展速率、几何形状、应变能释放速率、应力强度因子(SIF)等之间的关系,用于近似构件的断裂强度计算。在裂纹分析中,引用不同模型来描述相对于荷载加载的不同情况[4]的裂纹扩展和传播。不同荷载情况下的模型见图12 裂纹萌生寿命分析
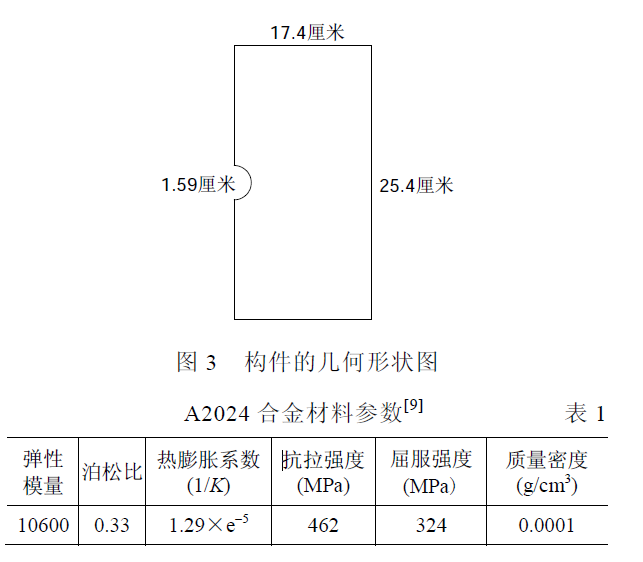
在预测裂纹萌生的荷载周期数时,必须定义局部参数,如应力、应变和能量类型(例如应变能的密度)。疲劳可以分为两种类型,高周期疲劳和低周期疲劳。在高周期疲劳中,应力水平较低,大部分疲劳寿命花在裂纹萌生中。在低周期疲劳中,应力水平较高,裂纹扩展过程占主导地位。本文通过有限元法来预测疲劳裂纹萌生寿命,并且建立数值模拟的方法来验证疲劳寿命。基于S-N曲线的裂纹萌生寿命预测方法在工程中常用Basquin[5]公式,为:在疲劳试验中通常包括对试件或整体结构[7]施加高周或低周循环交替荷载,如图2 所示。Von-Mises 应力是一种常用的应力表示量,用于定义失效标准。通常我们需要时刻保证被施加荷载的元素中的Von-Mises 应力的最大值小于构件材料本身的屈服强度[8]。构件尺寸为25.4×12.7×1.59 cm(图3),试件上有直径为1.59 cm 的半圆形缺口。构件材料为A2024 合金,其特性见表1。
利用动力力学函数创建的时间-数值函数曲线如图4,预估的S-N 曲线见图5。通过反复改变时间-数值函数,从而得到表2中的以下结果:从表 2 获取数据后,以应力振幅为y 轴,寿命周期为x 轴并以对数形式表示,从而得到修正后的S-N 函数曲线(图6): 
 MIDAS NFX 可以用来计算疲劳寿命的周期数,但不能用于计算出裂纹扩展寿命。在这里,AFGROW 将被用来计算裂纹的扩展寿命。计算裂纹扩展寿命时最常用的参数是应力强度系数(SIF),可由式(9)得到。在AFGROW 软件中,提供了两种获得SIF 的方法,一种是通过已知的校正参数,另一种是通过归一化应力得到β 校正参数[10]。
MIDAS NFX 可以用来计算疲劳寿命的周期数,但不能用于计算出裂纹扩展寿命。在这里,AFGROW 将被用来计算裂纹的扩展寿命。计算裂纹扩展寿命时最常用的参数是应力强度系数(SIF),可由式(9)得到。在AFGROW 软件中,提供了两种获得SIF 的方法,一种是通过已知的校正参数,另一种是通过归一化应力得到β 校正参数[10]。 式中:K 为应力场强度系数,应力强度因子;σ为应力;A 为裂纹尺寸;β 为Beta 校正系数,对于无限延伸的平板β=1。其中式(9)应力场强度系数单位为(N/m2) m=Pa m裂纹长度da 与应力周期dN 的关系Paris 法则如下:
式中:K 为应力场强度系数,应力强度因子;σ为应力;A 为裂纹尺寸;β 为Beta 校正系数,对于无限延伸的平板β=1。其中式(9)应力场强度系数单位为(N/m2) m=Pa m裂纹长度da 与应力周期dN 的关系Paris 法则如下: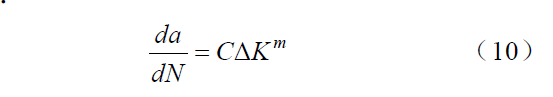
式中:C 为材料常数;ΔK 为应力强度因子的阀值。
通用的NASGRO公式如下:
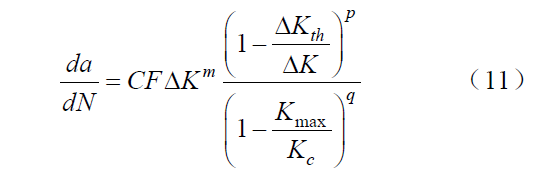
式中:F 为对裂纹闭合所做的贡献,参数n,p,q 被分别定义,式(11)在p=m,q=1 的情况下可以被简化为:式(12)可以清楚展示裂纹扩展与应力系数比R是相关的。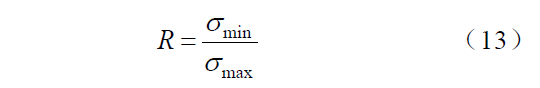
AFGROW 软件将三维建模问题转换为二维模型。要得到模拟应力强度因子可以分为两种方法。在本文中,我们只使用规范化应力的方法来得到几何因子。测试修正法计算(高斯积分法),如下图7 所示。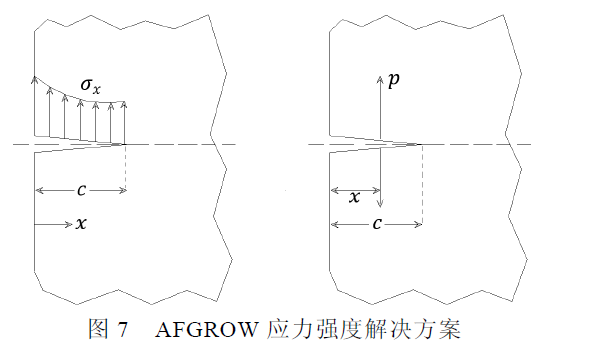
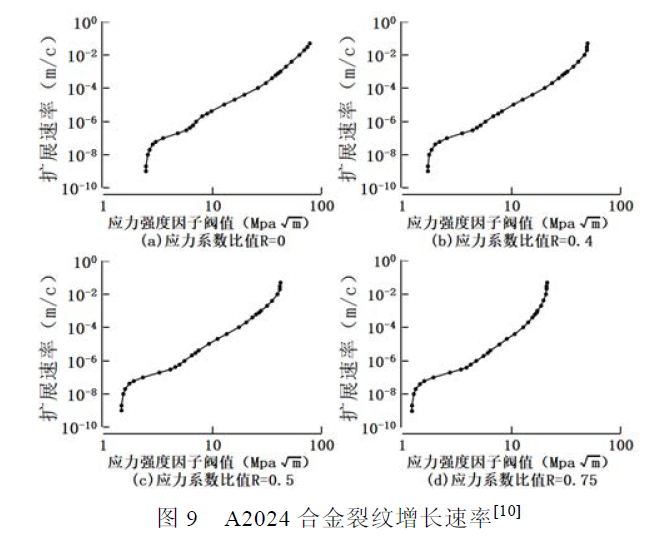
本文中的模型参数与同上图3,25.4×12.7×1.59 cm。在AFGROW 中我们将其转化为如图8所示英制模型参数。其材料参数选用与节2 同样材料参数。A2024合金的疲劳裂纹增长率如图9所示。图10为不同应力系数比值R下AFGROW缺口试件寿命计算结果,通过使用修正法和不使用修正法,我们可以得到不同的结果,见图11。
4 结语
本文采用了 MIDAS NFX 和AFGROW 结合起来利用有限元方法和数值模拟的方法对构件的疲劳寿命进行预估,弥补了单一软件使用的不足,其结果更加直观明了。针对不同的构件类型以及更加复杂的缺口模式需要未来更进一步的探索和研究。参考文献
[1] Brittle fracture of liberty ships[R], Oregon State: Failure Knowledge Database/100 Selected Cases, Report, 1943.[2] GRIFFITH, A.A., The phenomena of rupture and flow insolids[J]. Philosophical Transactions, Series A, 1920, 221:163-198.[3] IRWIN, G.R., Analysis of stresses and strains near the end of a crack traversing a plate[J]. Journal of Applied Mechanics, 1957, 24: 361-364.[4] Fracture mechanics, WIKIPEDIA, the three fracture modes, picture,[5] TSO-LIANG TENG, PENG-HSIANG CHANG, et al.Fatigue crack initiation prediction for a flat plate with a central hole[J]. Journal of Ccit, 2003, 32(1): 176.[6] G. FAJDIGAA, M. SRAMLB, Fatigue crack initiation,and propagation under cyclic contact loading[J]. Engineering Fracture Mechanics, 2009, 76(1):1320-1335.[7] 阎西康, 梁琳霄, 张玉淙. 受弯植筋梁疲劳损伤试验研究 [J]. 建筑结构, 2018, 48(1): 58-61, 76.[8] WEI CHENG CUI. A state-of-the-art review of fatigue life prediction methods for structures[J]. Journal of Marine Science and Technology, 2002, 7(1): 43-56.[9] E. SANTECCHIA, F. MUSHARAVATI, E. ZALNEZHAD, et al. A review on fatigue life prediction methods for metals[J]. Advances in Materials Science and Engineering, 2016, 2016(1): 1-26.[10] Afgrow aisp training[R]. Phoenix: Lextech, Report, 2018. 












 式中:K 为应力场强度系数,应力强度因子;σ为应力;A 为裂纹尺寸;β 为Beta 校正系数,对于无限延伸的平板β=1。
式中:K 为应力场强度系数,应力强度因子;σ为应力;A 为裂纹尺寸;β 为Beta 校正系数,对于无限延伸的平板β=1。