瞬态分析的时间积分法和开源软件Tempus
1. 引言:微分方程的种类
常微分方程ODE:未知函数和其导函数构成的等式。一阶的ODE的一般形式为

该式与方程(1)的区别在于该式包含一个不含导函数未知函数y, 也就是代数函数。在实际工程应用中,各色约束条件常常导入这样的代数函数项,一个常见的例子就是单摆问题中,单摆的长度不变条件导入的代数项。因此DAE方程在实际应用中更为常见。
DAE方程的一个特殊形式是下面的半显式方程

这是一个常微分方程方程。上述把微分代数方程转换为常微分方程的操作称为index reduction。由于我们经过一次微分运算就把方程(3)转换为常微分方程,方程(3)称为index 1的微分代数方程。相应地,常微分方程是index=0的微分代数方程。index用于分类并表述DAE方程的复杂程度。还存在其他index定义方法。上述定义方法(differentiation index)是最早,最常见的定义方法。
还有一点需要注意的是,在绝大多数文献中DAE写成方程(1), 而不是方程(2)的形式。此时的方程式DAE还是ODE可以通过对函数f对 x˙ 求导来判断。由于DAE内不包含所有的 x˙ 成分,其得到的矩阵将是非满秩,不可逆的。如果可逆的话,那就是ODE了。也就是说DAE不可直接求得 x˙ ,这一特点对方程性状和求解算法的设计都有很大的影响。
偏微分方程PDE
除去对时间变量的导数,如果方程内还包含对空间变量的导数。那就是偏微分方程了。对空间变量求导可以通过FEM,FVM,FDM来实现,与对时间的求导运算没有直接关系。因此,和PDE,ODE在时间维度的积分运算方法是完全相同的。当然基于时空一体的现代物理概念,所谓Space-Time Integration方法也是有的(比如这里),但是本文不涉及这一论题。

2. DAE方程数值积分求解器的使用方法
使用开源软件求解DAE的步骤如下。
1) 了解求解器的能力
比如DASSL只能求解index=0,1的方程(1), SUNDIALS (SUite of Nonlinear and DIfferential/ALgebraic Equation Solvers)中的IDA,IDAS则可以求解 implicit ODEs, index-1 DAEs和Hessenberg index-2 DAE方程。
2)修改你的方程
降低待解方程的index数和阶数使其转换为求解器可解类型。比如,如果你的方程含2阶时间导数 x¨ ,则上述DASSL,Sundials都不能求解,必须通过导入新变量将其降一阶。高index的方程一般难以求解,需要想办法降低。这里也有些技巧,比如把你大代数约束变换为导数约束。
其实这个问题对于空间导数也成立。比如本专栏介绍过的Cahn-Hilliard方程含四阶空间导数。我们就把它降为了2阶,不这样无法导入一般的有限元运算。
3)调用开源求解器
3. DAE方程数值积分算法
现在考虑用数值方法解方程(1)
 -
-

BDF(Backward Differentiation Formula)法

Runge-Kutta(RK)法
RK法是一种逐渐逼近割线方向的算法(参见下图)
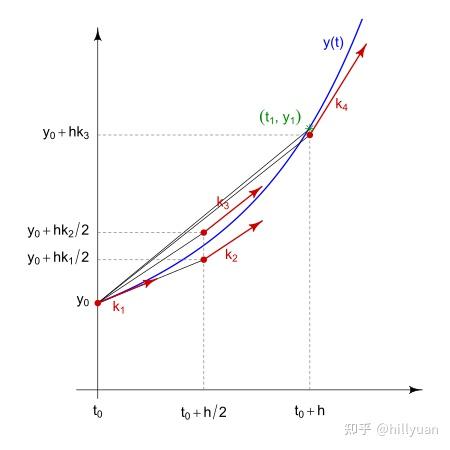 RK4法示意图
RK4法示意图
Runge-Kutta法的变种
如果待求变量x的维数为m,则求解方程(6)意味着需要求解一个 (s∗m)×(s∗m) 的联立方程。如果m值够大,这种算法就太奢侈了。需要给它减负。因为 aij 阵可以生成为一个下三角阵,其对角值有可能为同一值。利用这一特征可以产生不少算法,比如SIRK (Semi-Implicit Runge-Kutta methods),SERK (Semi-Explicit Runge-Kutta methods), DIRK (Diagonally-Implicit Runge-Kutta methods), SDIRK (Singly-Diagonally-Implicit RK methods), SIRK (Singly-Implicit Runge-Kutta methods)
IMplicit and EXplicit (IMEX)法
这种方法用于又刚度相差很大的成分构成的系统

其中F极刚,G极柔。这时把它们分成两个部分,分别用IMplicit和EXplicit来计算。
Newmark法
所有需要考虑加速度影响的计算都包含有时间的二阶导数。但是几乎所有的数值解析专著,DAEs方程解析软件都只考虑方程(1)。(好在本文下面将要介绍的开源软件Tempus包含这一功能)。这一现象是反映了数学界对振动分析工程师们的赤 裸裸的忽视!

Newmark法直接展开上式中的 x¨ 项而无需增加新的变量,这种做法的一个最直接的好处是待求自由度数比求解方程(1)时少一半,这对大型问题的解析而言是不容置疑的好处。至于其他有点,可以看看Newmark本人在这篇论文中是怎么说的。

-------------------------------------------------------------------------------------------
关于DAE方程数值积分算法的研究即使在现在仍然是一个非常活跃和充满挑战的领域。近年来有Geometric Integration, Variational time integration, Lie group time integration等种种新提法。另一方面,至今为止众多研究者们开发的通用,专用算法至少也有数十,上百种。你即使不搞开发只是使用这些算法,也需要对这些算法有大致的了解,这也是让人头疼的事。在本专栏的系列文章中,我们用到过如Runge–Kutta Implicit Midpoint这样不常用的算法,但是在大多数情况下我们用的是后退Euler。这种方法稳定性好,容易得到结果,但是也以导入过多的衰减而闻名。具体选择什么样的算法,还是需要具体问题具体分析。
4. 开源软件Tempus
与NOX/LOCA软件相同,
Tempus同样是按照外观设计模式组装的。按该模式组装的任何应用软件都可无障碍地调用该软件的所有功能。
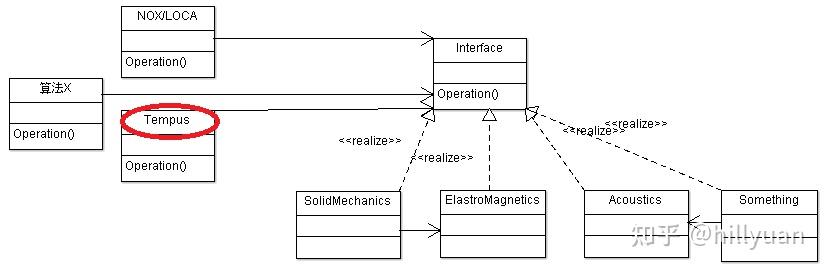
Tempus内实装得算法如下:
One-Step Methods:
- Forward Euler
- Backward Euler
- Trapezoidal MethodMulti-1Step Methods:
- BDF2Second-order PDE Methods:
- Leapfrog
- Newmark Implicit a-Form
- Newmark Implicit d-Form
- Newmark Explicit a-Form
- HHT-AlphaExplicit Runge-Kutta Methods:
- RK Forward Euler (RK1)
- RK Explicit 4 Stage
- RK Explicit 3/8 Rule
- RK Explicit 4 Stage 3rd order by Runge
- RK Explicit 5 Stage 3rd order by Kinnmark and Gray
- RK Explicit 3 Stage 3rd order
- RK Explicit 3 Stage 3rd order TVD
- RK Explicit 3 Stage 3rd order by Heun
- Merson 4(5) Pair
- RK Explicit Midpoint
- RK Explicit Trapezoidal or Heuns Method
- RK Explicit Ralston or RK2
- Bogacki-Shampine 3(2) Pair
- SSPERK22 (SSPRK2)
- SSPERK33 (SSPRK3)
- SSPERK54
- General ERKImplicit Runge-Kutta Methods:
- RK Backward Euler
- DIRK 1 Stage Theta Method
- RK Implicit Midpoint
- RK Implicit 1 Stage 1st order Radau IA
- RK Implicit 2 Stage 2nd order Lobatto IIIB
- SDIRK 1 Stage 1st order
- SDIRK 2 Stage 2nd order
- SDIRK 2 Stage 3rd order
- SDIRK 3 Stage 2nd order
- EDIRK 2 Stage 3rd order
- EDIRK 2 Stage Theta Method
- SDIRK 3 Stage 4th order
- SDIRK 5 Stage 4th order
- SDIRK 5 Stage 5th order
- SSPDIRK22
- SSPDIRK32
- SSPDIRK23
- SSPDIRK33
- SDIRK 2(1) Pair
- RK Trapezoidal Rule or RK Crank-Nicolson
- General DIRKImplicit-Explicit (IMEX) Methods:
- IMEX RK 1st order
- SSP1_111
- IMEX RK SSP2 (SSP2_222)
- IMEX RK SSP3 (SSP3_332)
- SSP2_222_L
- SSP2_222_A
- IMEX RK ARS 233
- ARS 233
- General IMEX RK
- Partitioned IMEX RK 1st order
- Partitioned IMEX RK SSP2
- Partitioned IMEX RK ARS 233
- General Partitioned IMEX RK
参考文献
Brenan, K. E., Campbell, S. L., and Petzold, L. R., The Numerical Solution of Initial Value Problems in Differential-Algebraic Equations, Elsevier Science Publishing Co., New York, 1989
Uri M. Ascher and Linda R. Petzold: Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations, Society for Industrial and Applied Mathematics, 1998
Achim Ilchmann, Timo Reis: Surveys in Differential-Algebraic Equations IV, Springer, 2017




