非线性方程求解算法与开源软件NOX
非线性方程:f(x)=0是最简单,最基本的非线性方程。其求解器很多,比如说Lapack中的函数DNQSOL, GSL中的相应函数,Sundials软件中的KINSOL等。但是本文无意于一般性的非线性方程求解器,而只是将注意力放在可进行大型并行计算的非线性方程求解器上。注意到在前面的文章中,我们导入了一个一般性非线性方程求解器的外观,或者说窗口类但是并未导入任何求解器,在下面的文章中,我们将逐步补足相应的算法软件,非线性方程f(x)=0求解器NOX(Nonlinear Object-Oriented Solutions)是第一个被导入的求解器软件。
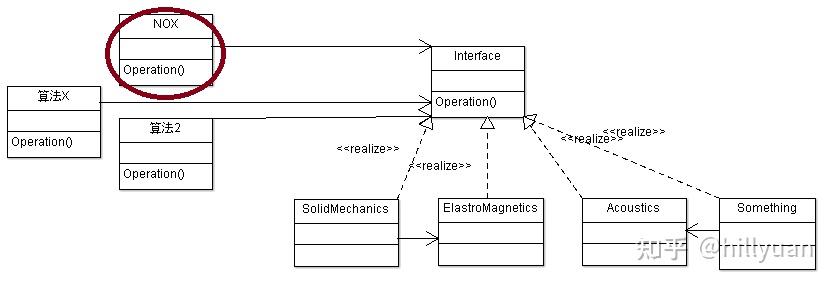 图1
图1非线性方程f(x)=0的求解方法有数种,比如说
Fixed Point迭代法
Bisection search法
The Secant Method
Inverse quadratic interpolation
Newton-Raphson法
但是对大型计算而言,我们往往只能看到Newton及其衍生出来的Newton-Like方法。比如说PETSc中实装的方法如下
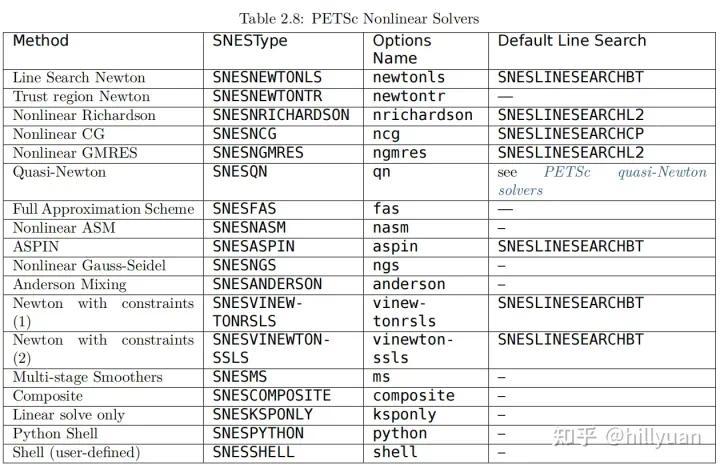 图2 PETSc中实装的非线性方程求解器
图2 PETSc中实装的非线性方程求解器下面我们捋一捋开源软件
NOXdocs.trilinos.org/dev/packages/nox/doc/html/index.html
中实装的方法。
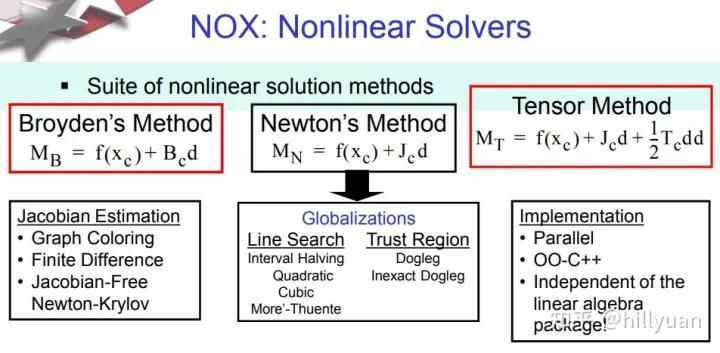 NOX构成[1]
NOX构成[1]注意:上图并不能概括NOX的全部实装。如下述Anderson accelerated fixed point法,Pseudo-Transient法都不包括在上图内。
0. Newton法

但是Newton法只有在初值选在根值附近,Jacobian性质够好的情况下才能求得方程的根。在上面介绍过的PETSc和NOX软件中实装的都是经过修正的Newton-like方法。
1. Line Search Methods

2. Trust Region法
Trust Region法 用下面的公式替代公式(2)
 不同信赖范围值得到不同的Cauchy点[2]
不同信赖范围值得到不同的Cauchy点[2]Cauchy点的位置并未考虑(3)式中B的影响。采用Cauchy点的Trust Region法先计算Cauchy点,然后使用 Bk 计算一个新的搜索方向。NOX采用的Dogleg法的计算方法式 pB=−B−1g
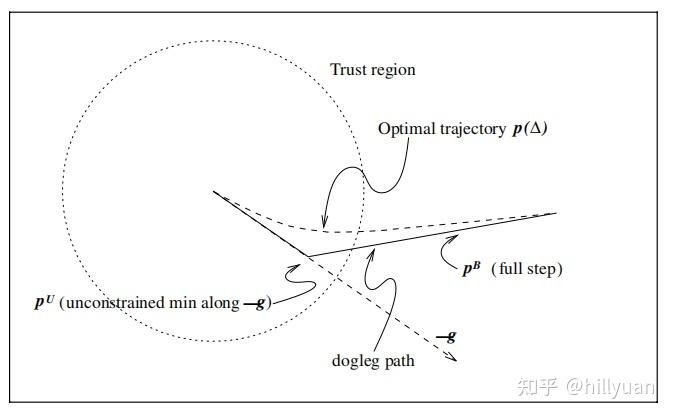 Dogleg法[2]
Dogleg法[2]3. Tensor法

4. Anderson accelerated fixed point[3]
经过加速的不动点法。
5. Pseudo-Transient法[4]
Pseudo-Transient(Ψtc )法是一种基于求解PDE稳定状态解的方法。

参考文献
1) Mark Hoemmen: An Overview of Trilinos, 2014
2)Jorge Nocedal,Stephen J. Wright : Numerical Optimization,Springer,2000
3) HE Walker, P Ni: ANDERSON ACCELERATION FOR FIXED-POINT ITERATIONS, 2011, SIAM J. NUMER. ANA
4)CT Kelly, DE Keyes: Convergence Analysis of Pseudo-Transient Continuation, 1998, SIAM J. NUMER. ANA
5)BW Bader: Tensor-Krylov Methods Large-Scale Systems of Equations for Solving Nonlinear Equations, 2004, SAND2004-1837




