自动求导运算在有限元软件开发中的应用
0. 引言
微分求导运算时最为常见的数学运算之一,其应用肯定不止于有限元软件。本文主要涉及的自动微分运算(Automatic Differentiation / Algorithmic Differentiation)近年来的急速普及就应该主要归功于其在人工智能,优化设计方面的应用。本文标题中的有限元软件只是为了注明本文中的用例主要出自有限元软件设计。
1. 求导运算方法种种

当 f 函数形式够简单,而你有足够的数学素养,你可以直接写下Jf 的表达式。但是这不是本文的目的。本文只考虑借助于计算机运算的求导方法。
差分运算: 逃脱不了被截断,减消数值误差夹击的命运,不可避免地带来数值误差。
Complex-Step Derivative : 如果 f 是解析函数,我们可以使用下述公式
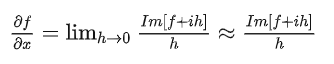
来计算 f 的导数。由于该公式不包含减法运算,所以没有减消误差。
Symbolic differentiation: 通过利用求导运算的链式法则将复杂的函数求导过程分解为基本函数形式,符号运算可以直接得到导数表达式。如果我们在此键入
derivative x^2*cos(x-7)/(sin(x))
即可以得到
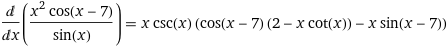
这种方法高大上,无数值误差。但是效率低。
自动导数计算 Automatic Differentiation : 与Symbolic Differentiation(SD)相同, Automatic Differentiation(AD)也利用求导运算的链式法则将复杂的函数求导过程分解为基本函数形式并取其导数。但是AD不处理符号,返回的是导数值。该方法无上述截断,减消数值误差。计算效率也高。
2. 非线性有限元求解
考虑使用有限元求解如下抽象问题

使用Newton-Raphson法求解此方程,其公式为

3. 使用Sacado自动导数计算技术的大规模有限元计算
现在也已公开的开源自动导数计算软件众多。
Community Portal for Automatic Differentiationwww.autodiff.org/
有限元开发工具libmesh,有限元软件Moose(都是通过使用开源软件MetaPhysicL)也导入了这一功能。我们的有限元软件使用Sacado,因为它与异构式并行计算平台Kokkos同属Trilinos软件群,有很好的亲和性,可以方便的通过使用Kokkos快速开发高效的含自动导数计算的大型并行计算程序。
3.1 使用Sacado开发有限元软件的具体做法
如上所述,我们只在单元层面上使用Sacado。在单元层面上使用Sacado,我们实际上只要做一件事,写出单元上的残差计算公式(1)。如此单元的刚度阵(也就是上面所示Jacobian矩阵),Hessian矩阵都可以通过Sacado自动得到。这是怎么做到的?让我们看看下面的例子。
下面的例子用于计算单元内的 ∫Ωk∇T∇δTdΩ 。这样的计算在有限元中很常见,比如热传导项。
template< typename ScalarT>evalResidual( std::size_t cell ){
Kokkos::View<ScalarT****, Layout, ExecSpace> weightedGradBasis;
Kokkos::View<ScalarT***, Layout, ExecSpace> gradT;
ScalarT k;
Kokkos::View<ScalarT**, Layout, ExecSpace> residual;
for (int basis=0; basis < numBases; basis)
{
residual(cell, basis) = 0.0;
for (int qp=0; qp < numQP; qp) {
for (int dim=0; dim < numDims; dim) {
residual(cell, basis) = k * grad_pr_(cell, qp, dim) * weightedGradBasis(cell, basis, qp, dim);
}
}
}}可以一眼看出上面的程序计算了residual值。但是注意这是一个带模板参量的函数,它可以实现多种计算。
evalResidual<double>() 计算单元内残差
evalResidual<Sacado::Fad::DFad<double>>() 计算单元的刚性矩阵
evalResidual<Sacado::Fad::DFad<Sacado::Fad::SFad<RealType,1>>() 计算单元的Hessian矩阵。
3.2 如何实现并行计算
上面的程序用到了Kokkos的数据结构,但是没有用到Kokkos的并行计算功能。我们只需稍加修改,就可以使用https://www.fangzhenxiu.com/post/5397945/。
template< typename ScalarT>
evalResidual()
{
Kokkos::View<ScalarT****, Layout, ExecSpace> weightedGradBasis;
Kokkos::View<ScalarT***, Layout, ExecSpace> gradT;
ScalarT k;
Kokkos::View<ScalarT**, Layout, ExecSpace> residual;
typedef Kokkos::RangePolicy<ExecSpace> Policy;
Kokkos::parallel_for(
Policy( 0,num_cell ),
KOKKOS_LAMBDA( const int cell )
for (int basis=0; basis < numBases; basis)
{
residual(cell, basis) = 0.0;
for (int qp=0; qp < numQP; qp) {
for (int dim=0; dim < numDims; dim) {
residual(cell, basis) = k * grad_pr_(cell, qp, dim) * weightedGradBasis(cell, basis, qp, dim);
}
}
}
);
}4. 结言
本文介绍了用自动求导运算计算单元刚阵的方法。但是如引言中所述,其应用并不止于此。相对而言,优化计算,Sensitivity Analysis等才更像是其一展身手的舞台。本文并不包含这方面的内容,希望以后能有机会补上相应的介绍。




