多物理场有限元软件的硬件加速性能评价
Device Acceleration Performance of a FEM software using Kokkos
第一次测试多物理场有限元软件(软件名待定)的并列计算功能,结果如下。
1. 基本设计
各计算节点间的通信采用MPI, 节点内通过调用Manycore Device Performance Portability Library Kokkos来实现在不同硬件平台上的并行加速计算功能。
 图1 并行计算功能的基本设计
图1 并行计算功能的基本设计2. 用于测试的硬件环境
一般家庭用PC
 图2 主板构成
图2 主板构成图形卡为入门级的游戏卡GeForce GTX 1050 Ti, 性能如下。这种图卡不是用来做科学计算的,其性能不好期待,仅用于功能测试。
| NVIDIA CUDA® Cores | 768 | |
| Memory Speed | 7 Gbps | |
| Standard Memory Config | 4GB | |
| Base Clock (MHz) | 1290 | |
| Computer Capability | 6.1 |
表1 图形卡性能
3 测试问题
简单的稳态热传导问题。棒材的一段指定温度,另一端赋予对流边界条件,其他部分边界绝热。材质设定为定值。这是一个线性问题。用来测试计算程序各个部分的时耗。
 图3 计算结果:温度分布
图3 计算结果:温度分布单元数270000,节点数289261
4 测试结果
4.1 Cuda vs OpenMP
使用GPU(Cuda)和CPU(OpenMP并行线程=4)进行比较计算。
本计算采用开源库Trilinos内线性方程组求解器Belos内的CG法,Trilinos内于预处理库Ifpack2内的不完全LU分解预处理ILUT的结果如下
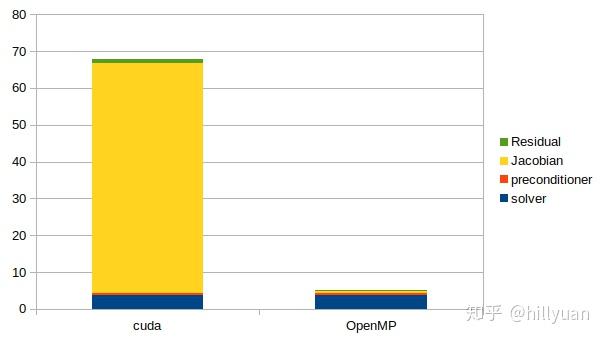 图4 计算时间(s)--solver: 求解器时间;preconditioner:预处理时间 Jacobian: 刚度阵计算时间;Residual: 残差计算时间
图4 计算时间(s)--solver: 求解器时间;preconditioner:预处理时间 Jacobian: 刚度阵计算时间;Residual: 残差计算时间1) 采用GPU计算单元积分计算(刚度阵&残差计算)速度极慢,虽然有高速组装刚度阵的报告[1],但是其实现颇有可疑之处。文献[2]的方法也许值得一试?
参考here。
2)但是用GPU来求解线性方程组看来效果不错。尤其是考虑到用一个低档的硬件可以做到这种程度。
近期内可以考虑用CPU组装刚度阵 and 用GPU求解方程。
4.2 线性方程组求解器Cuda vs OpenMP
采用Cuda和OpenMP求解线性方程组时的计算时间。注意各种求解器的参数选择和Kokkos对内存使用的管理参数对求解时间也有很大影响。本计算并未考虑这些问题。
本计算没有采用precondition计算, OpenMP线程=4。
| OpenMP | CUDA | |
| Block CG | 1.779 | 0.7828 |
| Block GMRES | 271.6 | 33.21 |
| Pseudo Block GMRES | 270.1 | 32.77 |
| Pseudo Block CG | 1.809 | 0.7784 |
| RCG | 3.7 | 1.11 |
| GCRODR | 24.16 | 5.473 |
| MINRES | 8.243 | 3.51 |
| TFQMR | 3.53 | 1.652 |
| BiCGStab | 3.036 | 1.4 |
| PCPG | 2.336 |
表2 线性方程组求解时间(s)
由于上面GMRES计算速度太慢,看一看precondition计算的效果 。
| OpenMP | CUDA | |
| Jacobi relaxation | 43.68 | 5.743 |
| Gauss-Seidel relaxation | 82.37 | 31.02 |
| Chebyshev | 8.621 | 1.792 |
| ILUT | 16.8 | 5.424 |
| RILUK | 9.333 | 5.448 |
| Additive Schwarz | 17.47 | 6.857 |
表3 当求解器为Block GMRES时,导入precondition计算后的线性方程组求解时间(s)
总体来看,GPU的跑速好于CPU,如果能换上一个好一点的GPU硬件,这是一个很不错的选择。
4.3 OpenMP计算的scalability
以1CPU的计算时间为基准,理想情况下2cpu时计算时间因为其1/2,4cpu时计算时间因为其1/4。该理想值在下图黄线所示。实际的增速见下图(蓝线)。
计算条件:Block CG 无precondition计算, 自由度数320000时的实际计算时间见下图橙色线。可见其非常接近于理想值,其效果尚可。
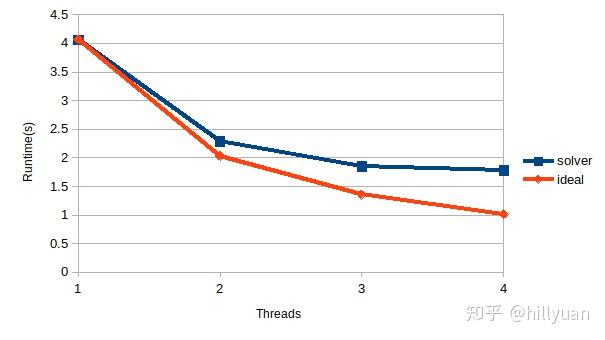 图5 多线程计算时线性方程求解器的计算时间(PC机结果)
图5 多线程计算时线性方程求解器的计算时间(PC机结果)图6为第4.4节所示专业计算机上的结果(自由度数=1120021, 求解器=Block CG)。这时计算效率就要好不少。
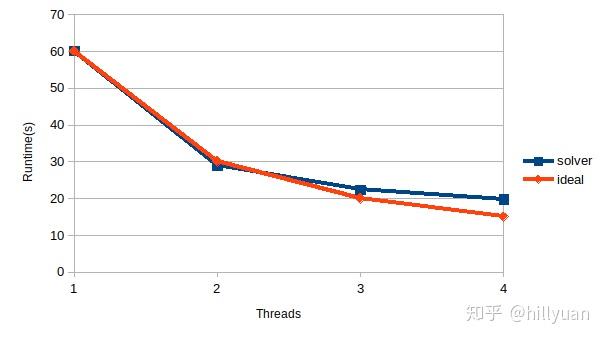 图6 多线程计算时线性方程求解器的计算时间(并行机结果)
图6 多线程计算时线性方程求解器的计算时间(并行机结果)4.4 MPI计算的scalability
本测试在下述科学计算专用并行机上进行。
Machine (190GB total)
Package L#0
NUMANode L#0 (P#0 94GB)
L3 L#0 (17MB)
L2 L#0 (1024KB) L1d L#0 (32KB) L1i L#0 (32KB) Core L#0 PU L#0 (P#0)
L2 L#1 (1024KB) L1d L#1 (32KB) L1i L#1 (32KB) Core L#1 PU L#1 (P#2)
L2 L#2 (1024KB) L1d L#2 (32KB) L1i L#2 (32KB) Core L#2 PU L#2 (P#4)
L2 L#3 (1024KB) L1d L#3 (32KB) L1i L#3 (32KB) Core L#3 PU L#3 (P#6)
L2 L#4 (1024KB) L1d L#4 (32KB) L1i L#4 (32KB) Core L#4 PU L#4 (P#8)
L2 L#5 (1024KB) L1d L#5 (32KB) L1i L#5 (32KB) Core L#5 PU L#5 (P#10)
L2 L#6 (1024KB) L1d L#6 (32KB) L1i L#6 (32KB) Core L#6 PU L#6 (P#12)
L2 L#7 (1024KB) L1d L#7 (32KB) L1i L#7 (32KB) Core L#7 PU L#7 (P#14)
L2 L#8 (1024KB) L1d L#8 (32KB) L1i L#8 (32KB) Core L#8 PU L#8 (P#16)
L2 L#9 (1024KB) L1d L#9 (32KB) L1i L#9 (32KB) Core L#9 PU L#9 (P#18)
L2 L#10 (1024KB) L1d L#10 (32KB) L1i L#10 (32KB) Core L#10 PU L#10 (P#20)
L2 L#11 (1024KB) L1d L#11 (32KB) L1i L#11 (32KB) Core L#11 PU L#11 (P#22)
HostBridge
PCI 00:11.5 (SATA)
PCI 00:17.0 (SATA)
Block(Removable Media Device) "sr0"
PCIBridge
PCIBridge
PCI 03:00.0 (VGA)
HostBridge
PCIBridge
PCI 18:00.0 (RAID)
Block(Disk) "sda"
PCIBridge
PCI 19:00.0 (Ethernet)
Net "em1"
PCI 19:00.1 (Ethernet)
Net "em2"
PCIBridge
PCI 1a:00.0 (Ethernet)
Net "em3"
PCI 1a:00.1 (Ethernet)
Net "em4"
Package L#1
......
以下Package若干
自由度数=1120021, 求解器为Block CG, 无precondition计算
 图7 采用4并行计算是的网格分区(不同颜色代表不同计算区域)
图7 采用4并行计算是的网格分区(不同颜色代表不同计算区域)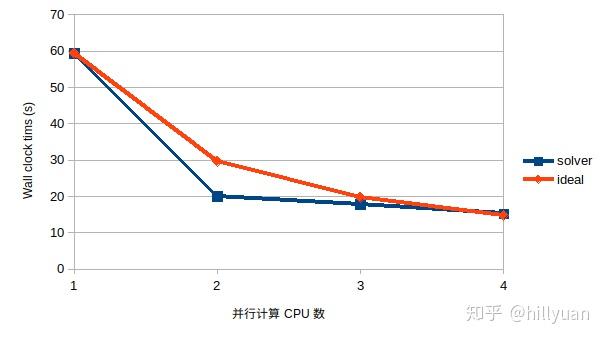 图8 并行计算时间
图8 并行计算时间在并行CPU数较少时,并行计算效果大于理想值,是可以满意的结果。
4.5 MPI/OpenMP混合计算
使用4.4节的算例和相同硬件,比较纯MPI计算和MPI/OpenMP混合计算的计算效率。
MPI(1Node∗4CPU/Node)MPI OpenMP(2Node∗2CPU/Node)ClockTime(s)15.254.96
MPI/OpenMP混合计算的结果似乎过好了。计算好像没有问题,但是不好解释,现在只好理解为第2Node多出的17M L3 Cache起的作用。
暂时把实际的输出记录留存于下:
MPI only
TimeMonitor results over 4 processors
Timer Name MinOverProcs MeanOverProcs MaxOverProcs
Belos: BlockCGSolMgr total solve time 15.25 (1) 15.26 (1) 15.28 (1)
MPI OpenMP
TimeMonitor results over 4 processors
Timer Name MinOverProcs MeanOverProcs MaxOverProcs
Belos: BlockCGSolMgr total solve time 4.956 (1) 4.96 (1) 4.962 (1)
结论
除去用GPU计算刚度阵的计算速度过慢以外,其他结果都大致令人满意。
参考文献
[1] Speeding up a Finite Element Computation on GPU
[2] GPU-warp based finite element matrices generation and assembly using coloring method




