谈一谈混凝土的本构关系:浅析混凝土本构行为的连续体唯像模型
 [1] 封面
[1] 封面1. 本文的目的和范围
混凝土的行为表述目前仍然是经验的世界。本文仅涉及混凝土本构行为的连续体唯像模型,不涉及混凝土内的化学反应和发热(暨由此而产生的时效和自收缩),不涉及如smeared crack model这样的假想细观模型。最后,为了简化问题,本文仅考虑混凝土的静态变形行为,不考虑应力-应变曲线的时滞,蠕变,也就是变形的粘性成分。
2. 混凝土变形特征
大量的实验数据是建立维像模型的基础,在下面的参考文献[1]~[7]中列举了大量的实验数据,在此不再赘述。
 图1 [7] p40
图1 [7] p40从上图中我们可以看到如下特征
外力消除后,留下不可恢复的变形。也就是说存在塑性变形。
途中的卸载- 重载过程,如果忽略时滞,并不影响材质(应力-应变曲线恢复原状)。可以认定为弹性变形。
杨氏模量渐渐变小。也就是说材料的承载能力降低。需要导入如损伤系数这样的概念来描述这一现象。
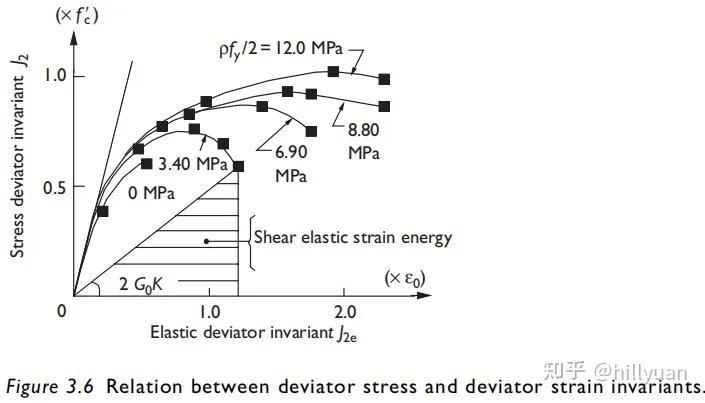 图2 受不同周向压力的受压圆柱的变形[1]p129
图2 受不同周向压力的受压圆柱的变形[1]p129混凝土受压能力强,受拉能力弱。也就是说其变形行为受到体积力的很大影响。上图为受到不同周向压力下轴向的应力-应变图。可以看出,周向力(图中以 ρfy 来表示)大时,轴向的可变形量也大。
综上所述,弹-塑-损伤模型也许是描述混凝土变形行为的可行模型。
2.1 弹性损伤本构方程
损伤用于表现材料承载能力的减小。导入损伤系数 ω ,弹性应力-应变关系可以写成 σ=D(ω):εe .此时ω可以是标量也可以是矢量。使用矢量可以来表示不同方向的损伤,使用标量时则假定损伤没有方向性·。
在大多数情况下,上面的式子简写为 σ=ωD:εe 。此时 ω≤1 为一个随着变形逐渐减小的标量。如何写出损伤系数的演化公式用来再现图1中卸载时的应力-应变曲线斜率则是广大实验工作者的课题了。
2.2 塑性屈服面
按照下面的原则构筑屈服函数
如果使用应力空间,屈服函数必须为应力不变量(如果屈服函数各向同性。就是三个应力不变量 I1,I2,I3 )的函数。如果使用应变空间,屈服函数必须为应力不变量(如果屈服函数各向同性。就是三个应变不变量 J1,J2,J3 )的函数。一般情况下,我们都用应力函数来表示屈服面,但是有的混凝土屈服函数(如参考文献[1],[5])是用应变来表示的。
需要注意屈服函数受到应力(应变)状态的很大影响。需要多取几组不同应力(应变)状态的屈服点。你的屈服函数必须落在这些屈服点之上.

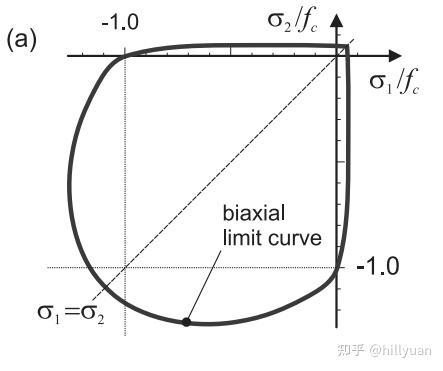 图3 应力空间上的屈服函数([3]p152,p154)
图3 应力空间上的屈服函数([3]p152,p154)应力(应变)硬化(软化)曲线
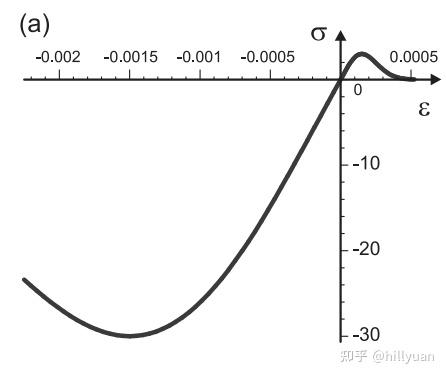 图4 应力(应变)硬化(软化)曲线([3]p.)
图4 应力(应变)硬化(软化)曲线([3]p.)2.3 本构方程推导
如果得到了上面的损伤和屈服函数,就可以经过简单的数学推导得到本构方程。
3. Maekawa本构方程[1]
在开源软件
hillyuan:介绍一个开源有限元软件FrontISTR15 赞同 · 5 评论文章
中导入了参考文献[1]中得到的混凝土本构方程(该部分未公开),下面结合上面的论述看看混凝土本构方程的具体实装。Maekawa本构方程是建立在应变空间的各向同性的本构方程。
3.1 弹性损伤
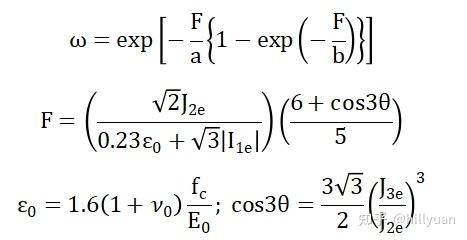
3.2 塑性变形
屈服函数的偏应变部分

屈服函数的体积应变部分

最后得到的本构方程如下*
(1)dσ=C:(I−L):dε

整个公式给我的印象是真够复杂。难以想象其创造者是怎么想出来的。这个不服不行!
3.3 验证计算
采用FrontISTR计算了三向受压圆柱问题。如图6·所示,其计算结果与理论解相同。
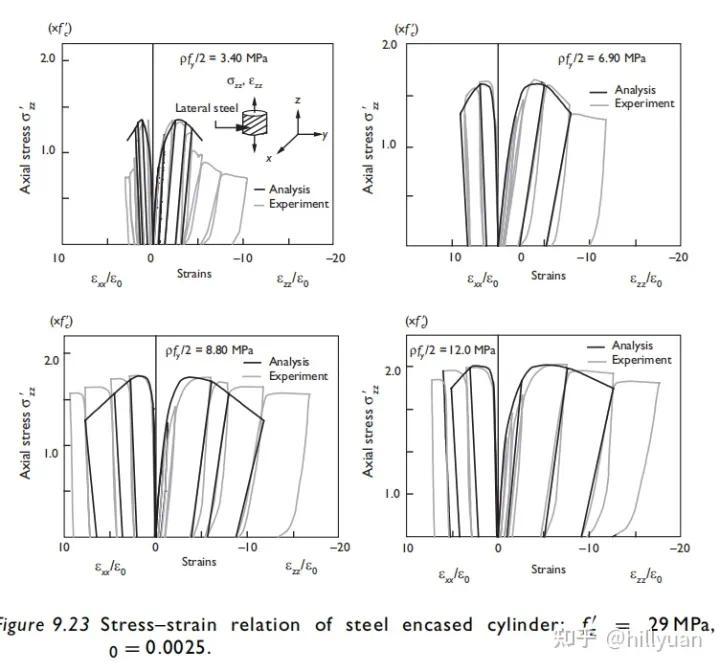 图5 三向受压圆柱的轴向变形实验结果
图5 三向受压圆柱的轴向变形实验结果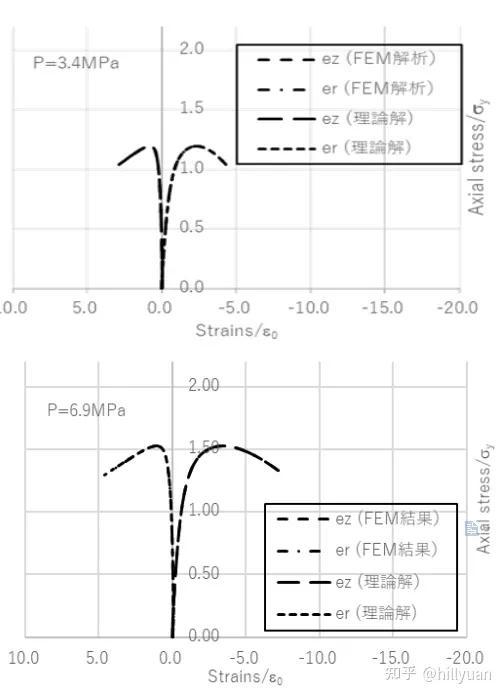 图6 理论解和有限元计算结果
图6 理论解和有限元计算结果附注*
本文所得到的混凝土本构方程虽然出自参考文献[1], 但是与其记载的公式并不相同。参考文献[1]给出的是一个可以继续简化的夹生公式。有意思的是有其他的研究者( 山下拓三,堀宗朗,小国健二,岡澤重信,牧剛史, 高橋良和:大規模有限要素法のためのコンクリート非線形構成則の再定式化, 土木学会論文集 A2(応用力学),vol.67, No.1, 145-154, 2011.)想把这个夹生饭煮熟,他们得到的公式确实简化了一些,但可惜是完全错误的。
参考文献
K. Maekawa, A. Pimanmas, H.Okamura: Nonlinear Mechanics of Reinforced Concrete, Spon Press, 2003
WK. Chen: Plasticity in Reinforced Concrete, J.Ross Publishing, 2007
Ulrich Häussler-Combe : Computational Methods for Reinforced Concrete Structures, Ernst & Sohn, 2015
P.H.Feenstra : Computational Aspects of Biaxial Stress in Plain and Reinforced Concrete, Delft Univ., 1993
Yuxiang Xing : CONSTITUTIVE EQUATION FOR CONCRETE USING STRAIN-SPACE PLASTICITY MODEL, New Jersey Institute of Technology, 1993
Practitioners' guide to finite element modelling of reinforced concrete structures: State-of-art report-FIB - F, Federation internationale du beton, 2008
Zhenhai Guo : Principle of Reinforced Concrete, Elsevier, 2014




