PiFlow关键提升——高超计算精度“稳了”!
摘
要
GoCart在高超音速的计算精度得到了工程师的认可,PiFlow作为GoCart的对标软件,在高超音速上的表现如何呢?
下面是两个标准高超算例,经过与专业高超结构网格解算器结果对比,求解欧拉方程时两个软件的气动力/力矩曲线结果99%吻合;欧拉方程(PiFlow)与N-S方程气动力/力矩曲线结果对比,阻力略微偏差,误差也在正常范围内,所以,PiFlow软件高超计算精度值得信赖!值得信赖!
案例1
高超声速飞行器——乘波体
外形结构:
高超声速飞行器由于其设备载荷与结构等原因,常常采用简单组合体外形,其中乘波体是比较典型的一类。外形结构如图1所示。
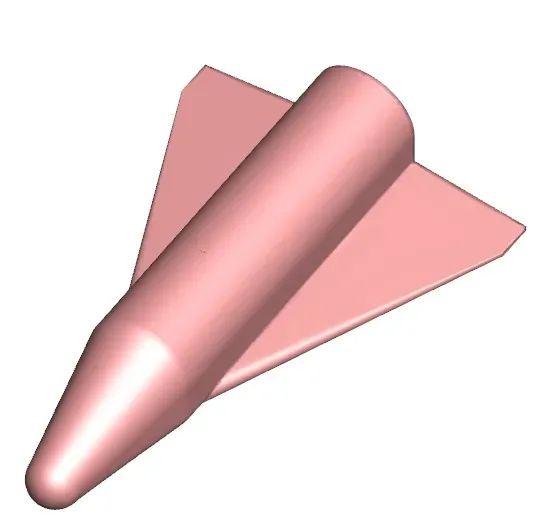
图1 乘波体外形
计算条件:
来流马赫数 | 6.5 |
飞行高度 | 30Km |
来流压力 | 1197.004 Pa |
来流温度 | 226.509K |
攻角 | -5°,0°,3°,5°,10°,15°,20°,25° |
侧滑角 | 0 |
参考长度 | 1 |
参考面积 | 1 |
力矩中心 | (0,0,0) |

计算网格:
计算区域为模型长度的8倍的立方体区域。边界条件四周为压力远场,物面使用滑移边界。网格参数如图2所示。

图2 网格参数设置
计算网格量87万,离散网格如图:

图3 机身切片网格

图4 机翼切片网格
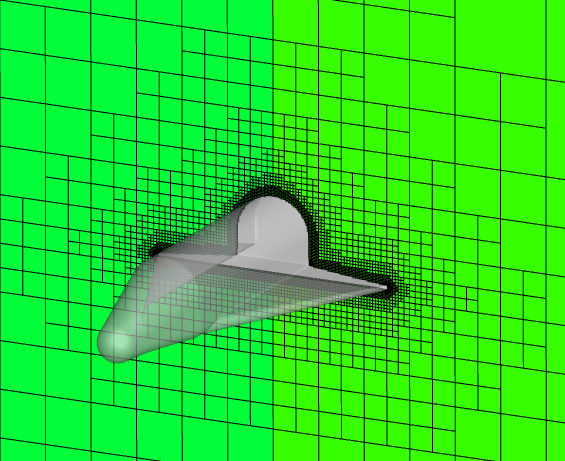
图5 X轴切片网格

计算结果:
解算时候采用欧拉稳态模型进行求解,计算格式为中心格式,计算工况根据以上提到的工况依次求解,最终获得PiFlow软件计算的气动力/力矩随攻角变化的曲线。
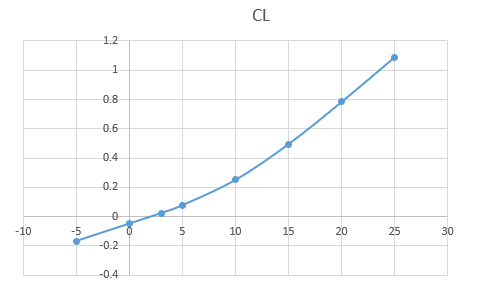

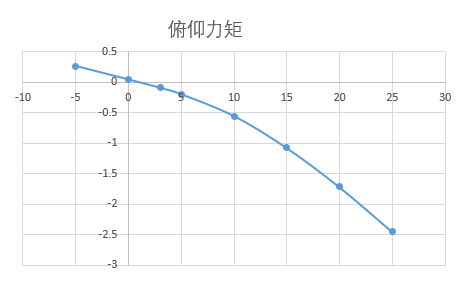

置信度:
为了验证PiFlow软件高超状态计算结果的正确性,因此与一款高超计算的专业软件进行对比,①该软件使用的是粘性方程,SST模型;②MUSCL-RoeRusanov混合空间离散格式求解欧拉方程;网格量100万左右结构网格。置信度对比图如下所示。

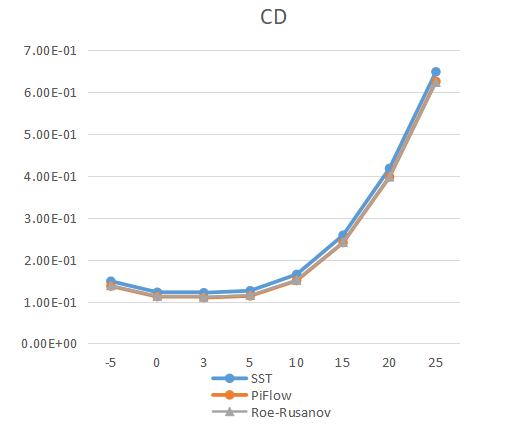
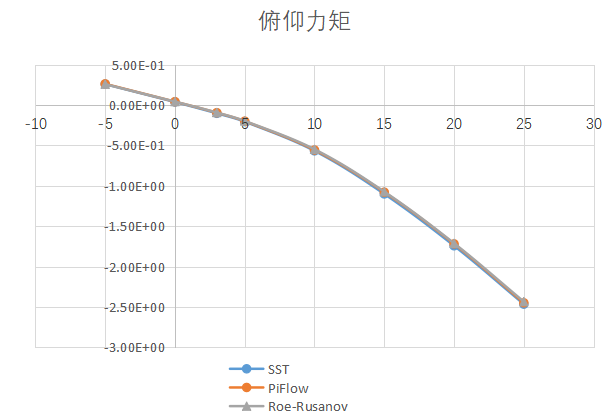

案例2
高超声速飞行器——钝锥
外形结构:
随着对飞行器更高速度、远距离的发展要求,本案例以典型旋成体球头钝锥为研究对象,进行高超音速数值模拟分析。钝锥外形结构如图1所示。

图1 钝锥外形
计算条件:
来流马赫数 | 10.6 |
来流压力 | 127.43 Pa |
来流温度 | 49.98K |
攻角 | 0°,5°,10°,15°,18°,20°,25°,30° |
侧滑角 | 0 |
参考长度 | 1 |
参考面积 | 1 |
力矩中心 | (0,0,0) |

计算网格:
计算区域为模型长度的8倍的立方体区域。边界条件四周为压力远场,物面使用滑移无穿透边界。网格参数如图2所示,

图2 网格参数设置
计算网格量67万,离散网格如图3所示:

图3 Y轴切面网格

计算结果:
解算时候采用欧拉稳态模型进行求解,计算格式为中心格式,计算工况根据以上提到的工况依次求解,最终获得PiFlow软件计算的气动力/力矩随攻角变化的曲线。
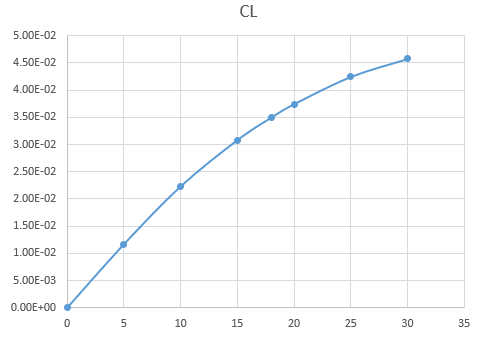



置信度:
为了验证PiFlow软件高超状态计算结果的正确性,因此与一款高超计算的专业软件进行对比,①该软件使用的是粘性方程,SST模型;②MUSCL-RoeRusanov混合空间离散格式求解欧拉方程;网格量100万左右结构网格。置信度对比图如下所示。

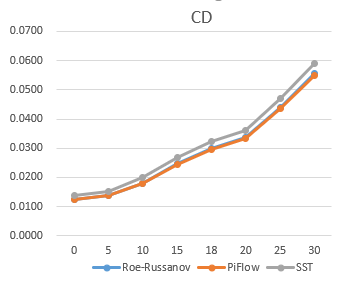


结论:
1)PiFlow软件在使用上方便快捷,网格自动化程度高,鲁棒性高。
2)从置信度曲线图可以说明PiFlow软件高超音速的计算能力,气动力与力矩指标曲线吻合度可以证明PiFlow软件的精度满足设计要求;两款软件同样求解欧拉方程曲线结果99%吻合;粘性方程与欧拉方程结果对比时,阻力有略微偏差,误差也在正常范围内。





