基于Digimat的混凝土等效弹性模量研究
作者:高真,曹鹏,李劲松
来源:水利水电技术第49卷2018年第5期
摘 要:在细观结构上混凝土可作为由水泥砂浆、粗骨料、界面、孔隙和微裂缝组成的多相复合材料,将含有孔隙和微裂缝的水泥砂浆作为基体,粗骨料和其包裹的界面作为夹杂相,建立大坝混凝土的细观力学模型。混凝土模型采用Digimat建立, 它是基于Eshelby夹杂理论,采用Mean Field均匀化的一种半分析方法,可对所有增强相为椭圆形拓扑的多相非线性材料进行快速准确的性能预测,获得刚度矩阵和工程常数。文中基于Digimat在骨料体积比分别为0.2,0.4,0.6和0.8时预测了混凝土等效抗拉和抗压弹性模量值以及分析了水泥砂浆弹性模量,粗骨料纵横比和孔隙所占水泥砂浆体积比对混凝土等效弹性模量的影响,通过比对表明该模型在一定程度上能够反映出细观上各项组成对混凝土弹性模量的影响。
引言
如今,无论是已建、正建还是待建的混凝土坝均已分布全国各地,其工程规模居世界前列,且地质条件复杂,工程难度大。另外,混凝土的物理力学性质不同于完整岩体,它存在抗裂性能差,建造期长,加固和改造困难等一系列问题,使得混凝土坝的建设和利用面临诸多困难,因此,对于混凝土物理力学性质的研究具有重要的意义。
随着计算机的发展,针对混凝土的静、动力学性质已有较多研究,目前对混凝土弹性常数的预测所采用的模型较多的是并联模型(Voigt模型)和串联模型(Reuss模型),但该模型只能得出等效模型的上下限,不能准确的预测混凝土的有效弹性模量。马怀发等未考虑孔隙对混凝土等效弹性模量的影响。马辉等从理论上得出了等效弹性模量的解析公式,但忽略了泊松比的影响,结果存在一定偏差。另外,研究混凝土的力学特性的试验也相对较多,但试验研究的成本高和耗时,且较难得出一般性规律。
混凝土作为多相复合材料,文中基于Digimat对混凝土等效弹性模量进行研究。Digimat是一种非线性多尺度复合材料与结构建模平台,它是基于Eshelby夹杂理论,采用Mean Field均匀化方法的多相材料非线性材料本构预测工具,在细观尺度上,它可以对所有增强相为椭圆形拓扑的多相材料进行快速准确的性能预测,获得刚度矩阵和工程常数,故可基于Digimat较为精确的预测出混凝土的等效弹性模量以及分析出各组相对混凝土等效弹性模量的影响。
混凝土均匀化方法
2.1 基本原理
解决力学问题时不能仅停留在细观尺度上,因此需区分两个尺度:细观尺度和宏观尺度,这两个尺度是通过代表性体积单元(RVE)来联系的。在宏观尺度上,对于每个宏观材料点(假设每个材料点是RVE的中心),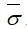 为宏观应力和
为宏观应力和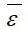 为宏观应变。细观尺度上有RVE区域
为宏观应变。细观尺度上有RVE区域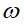 、体积
、体积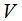 和边界条件
和边界条件 。RVE应该足够大来代表细观结构的非均质特性,但相对于整个材料来说也足够小。RVE在线性边界条件作用下,宏观上的应力和应变等价于RVE区域内细观应力
。RVE应该足够大来代表细观结构的非均质特性,但相对于整个材料来说也足够小。RVE在线性边界条件作用下,宏观上的应力和应变等价于RVE区域内细观应力 和细观应变
和细观应变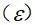 。文中采用平均场均匀化方法对混凝土进行分析,然而,平均场均匀化方法也有不足,它无法得出每个相中的应力和应变场数值。
。文中采用平均场均匀化方法对混凝土进行分析,然而,平均场均匀化方法也有不足,它无法得出每个相中的应力和应变场数值。
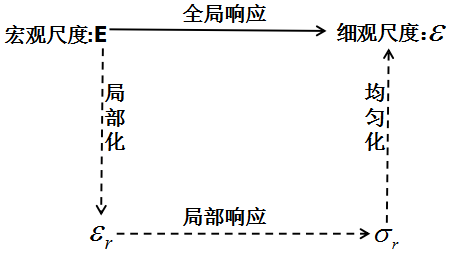
图1 平均场均匀化过程
图1为平均场均匀化方法的过程。(1)局部应变根据宏观应变计算;(2)局部应力根据局部应变和每个相的模型来计算;(3)宏观应力根据平均局部应力计算。
2.2 混凝土均匀化理论分析
细观力学将混凝土看作由界面包裹的粗骨料和含有孔隙和微裂缝的水泥砂浆组成的非均质复合材料。在RVE中,将界面包裹的粗骨料作为夹杂相和含有孔隙和微裂缝的水泥砂浆作为基体项,因宏观刚度是微观刚度的体积平均值,可通过应变集中张量定义来求得宏观刚度。
在RVE上对应力场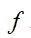 的平均化定义:
的平均化定义:
 (1)
(1)
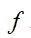 为RVE内部的细观应力场,
为RVE内部的细观应力场,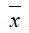 为宏观坐标点,
为宏观坐标点, 为细观坐标点。
为细观坐标点。
在基体和夹杂相上对应力场的平均化定义:
 (2)
(2)
式中0和1分别表示基体和夹杂相,
RVE、基体相和夹杂相应变场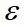 的体积平均关系为:
的体积平均关系为:
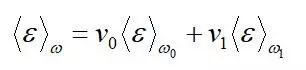 (3)
(3)
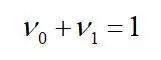 (4)
(4)
平均场均匀化模型可通过应变集中张量来定义:
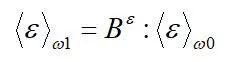 (5)
(5)
夹杂体应变的体积平均与整个RVE(宏观应变)的体积平均相关,通过应变集中张量来定义:
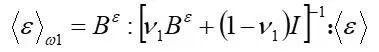 (6)
(6)
平均场均匀化模型是以Eshelby张量为基础,利用Eshelby解,在夹杂体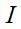 内部的应变是均匀的,且与远程应变相关:
内部的应变是均匀的,且与远程应变相关:
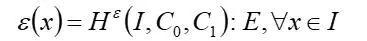 (7)
(7)
其中,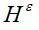 为单夹杂体的应变集中张量,定义为:
为单夹杂体的应变集中张量,定义为:
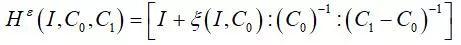 (8)
(8)
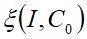 为Eshelby张量。
为Eshelby张量。
对于均匀化模型来说,宏观刚度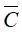 为:
为:
 (9)
(9)
2.3 混凝土模型
混凝土模型采用平均场均匀化方法,是基于Eshelby夹杂理论,等效颗粒运用Mori-Tanaka均化算法以及等效基体运用双夹杂均化算法。混凝土混合夹杂模型如图2所示,将含有孔隙和微裂缝的水泥砂浆作为等效基体,粗骨料和其包裹粗骨料的界面看作是球形等效颗粒,作为夹杂相,形成混凝土混合夹杂模型。为建立混凝土混合夹杂模型,假设混凝土各细观组成相材料都是理想均匀、各向同性的弹性材料,并且忽略骨料形状、级配的影响,采用同一粒径的球形颗粒模拟骨料。
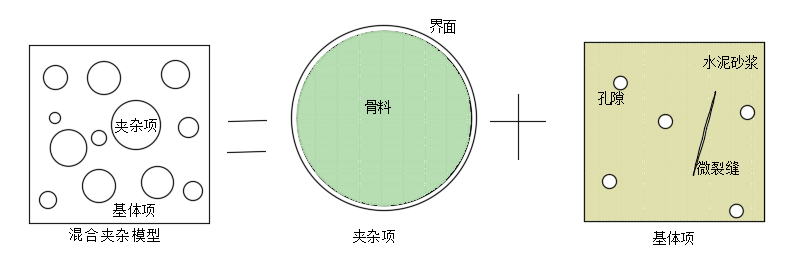
图2 混凝土混合夹杂模型
其中界面层包裹的骨料采用双夹杂模型,双夹杂模型如图3所示,它基于以下想法:刚度为 的夹杂体
的夹杂体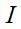 被由刚度为
被由刚度为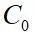 的材料包裹,在该材料之外的区域是刚度为
的材料包裹,在该材料之外的区域是刚度为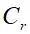 的基体材料。此时,真实RVE被由虚拟的复合材料所代替,该材料由刚度为
的基体材料。此时,真实RVE被由虚拟的复合材料所代替,该材料由刚度为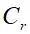 的参考基体和刚度为
的参考基体和刚度为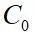 的夹杂体以及覆盖在其表层的刚度为
的夹杂体以及覆盖在其表层的刚度为 的材料所构成,因此称为双夹杂。
的材料所构成,因此称为双夹杂。
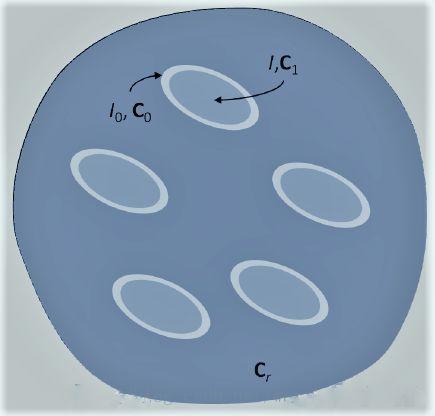
图3 双夹杂模型示意图
数值模拟以及结果对比
我想请大家来看这样一个图。这个图是从全球很多的经济体的增长历史中得到的数据。横轴表示的是某个国家在某个历史阶段的经济发展水平,纵轴表示的是这个国家在同样历史阶段的劳动生产率的增长速度。首先经济发展水平比较低的国家情况差异非常大,红色的这些点劳动生产率的增长速度非常快,白色的这些点劳动生产率的速度非常慢。红色的和蓝色的点,代表着实现了经济增长潜力的国家和地区,或者说最成功的经济体,它们的劳动生产率增长速度随着经济发展水平的提升在逐渐下降。
选择Stock的试验数据,根据建立的混凝土模型对其抗压弹性模量和抗拉弹性模量进行计算,通过与试验数据的比对验证该模型的有效性。Stock通过试验的方法测得数据如下:水灰比为0.5,水泥砂浆的抗压和抗拉弹性模量分别为、Em=1.34×104N/mm2、Ep=1.16×104N/mm2,水泥砂浆的泊松比为vm=0.25,粗骨料的弹性模量为Ea=7.45×104N/mm2、粗骨料的泊松比为va=0.15,界面层的弹性模量取为水泥砂浆弹性模量的0.4倍、泊松比为vi=0.3、厚度为粗骨料粒径的0.005,孔隙和微裂缝所占的混凝土体积比均取为1%。混凝土模型如图4所示,图(a)可以直观的显示混凝土的组成成分,图(b)对混凝土模型进行了网格划分,采用六面体网格,经计算该细观模型共有148202个单元和298654个节点。
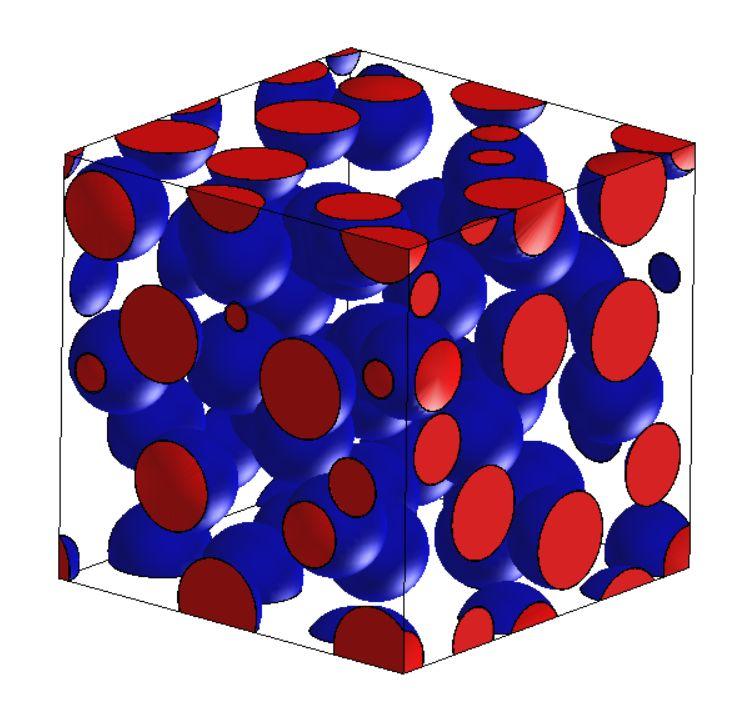
(a)
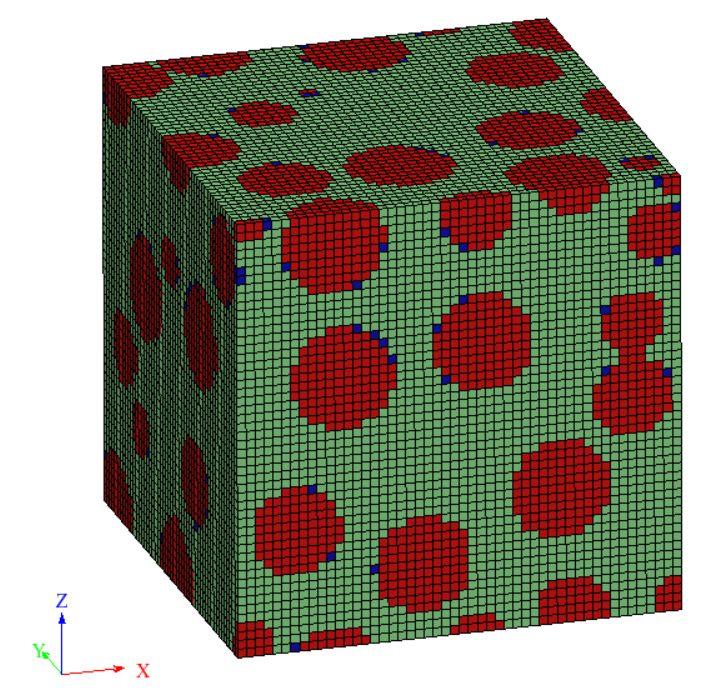
(b)
图4 混凝土模型
取粗骨料体积百分比为0.4,由均匀化方法得出混凝土的等效弹性矩阵如表1所示。
表1 混凝土的等效弹性矩阵
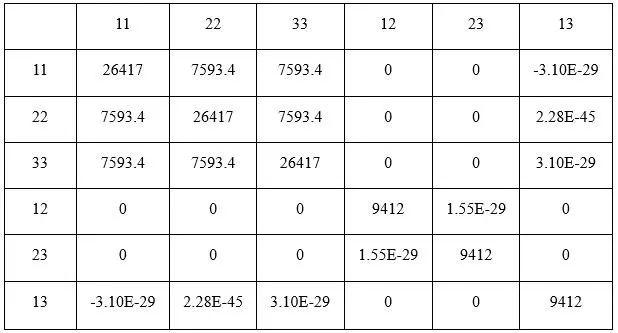
经过计算,混凝土泊松比为v=0.21,宏观抗压弹性模量为Ec=2.23×104N/mm2,而Stock等人得到的实验值为Ec=2. 32×104N/mm2,相对误差为3.9%。
其他参数不变,只改变粗骨料在混凝土中所占体积百分比,分别取0.2,0.4,0.6和0.8,抗压弹性模量值如表2所示,抗拉弹性模量值如表3所示。
表2 混凝土抗压弹性模量值 GPa
粗骨料体积比(%) | 试验测定值 | 模型预测值 | 误差/% |
0 | 13.4 | - | - |
20 | 15.8 | 16.9 | 7.0 |
40 | 23.2 | 22.2 | 4.3 |
60 | 30.7 | 30.0 | 3.6 |
80 | 39.1 | 41.9 | 5.1 |
表3 混凝土抗拉弹性模量值 GPa
粗骨料体积比(%) | 试验测定值 | 模型预测值 | 误差/% |
0 | 11.6 | - | - |
20 | 17.8 | 16.2 | 9.0 |
40 | 21.4 | 20.5 | 4.2 |
60 | 29.0 | 28.8 | 0.7 |
80 | 41.3 | 42.7 | 3.4 |
图5和图6分别给出在不同粗骨料体积比下,实验测定和模型预测的混凝土等效抗压弹性模量值和抗拉弹性模量值。结果表明,模型预测值和试验测定值相近,随着粗骨料体积比的增加混凝土的等效弹性模量成指数增加,粗骨料体积比相同时混凝土的抗压弹性模量大于抗拉弹性模量。
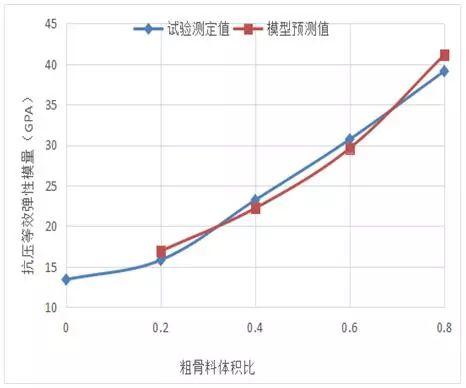
图5 试验测定和模型预测的混凝土等效抗压弹性模量
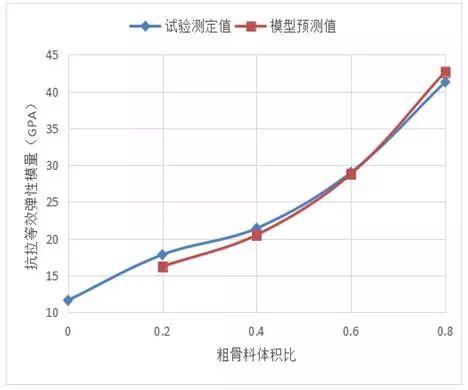
图6 试验测定和模型预测的混凝土等效抗拉弹性模量
在细观结构层次上,影响混凝土等效弹性模量的因素很多,文中运用混凝土混合夹杂模型分别预测出不同基体水泥砂浆的弹性模量、不同粗骨料纵横比和不同孔隙所占的水泥砂浆体积比对混凝土等效弹性模量的影响。
图7给出基体水泥砂浆的弹性模量分别为8.4GPa,13.4GPa和18.4GPa时对混凝土等效弹性模量的影响。结果表明,基体水泥砂浆的弹性模量对混凝土等效弹性模量的影响较大,随着水泥砂浆弹性模量的增加混凝土等效弹性模量随之增加。
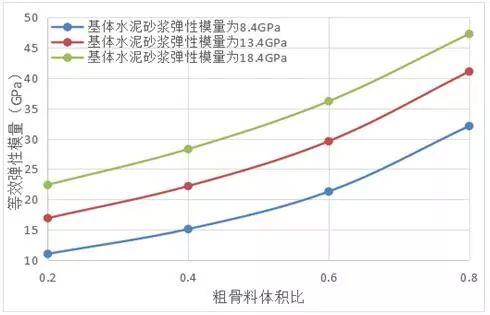
图7 水泥砂浆弹性模量对混凝土等效弹性模量的影响
上述实验测定值和模型预测值的前提是粗骨料纵横比为1.0(即为球形),为了进一步研究粗骨料对混凝土等效弹性模量的影响,预测了粗骨料的纵横比分别为1.0,1.2,1.4和1.6时混凝土的等效弹性模量值。图8给出不同粗骨料纵横比对混凝土等效弹性模量的影响。结果表明,在其他参数不变的情况下,随着粗骨料纵横比的增大混凝土等效弹性模量呈上升趋势。并且由图可知,当骨料体积比为0.2时,随着粗骨料纵横比的增大对混凝土等效弹性模量的影响并不太显著,但随着骨料所占体积比的增加,粗骨料纵横比对混凝土等效弹性模量有较大影响。
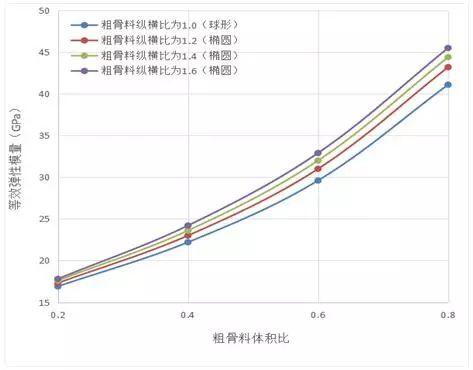
图8 粗骨料纵横比对混凝土等效弹性模量的影响
水泥在硬化过程中不可避免地会产生孔隙,同时,由于振捣不实、养护不好等原因也会在混凝土中留下孔隙,因此,在对混凝土进行细观数值分析的过程中,混凝土的孔隙也是一个不可忽视的重要影响因素。图9给出孔隙所占的水泥砂浆体积比分别为0.01,0.03和0.05时对混凝土等效弹性模量的影响。结果表明,孔隙所占水泥砂浆体积比对混凝土的等效弹性模量有密切的关系:在其他参数不变的情况下,随着所占水泥砂浆体积比的增大混凝土等效弹性模量呈下降趋势。
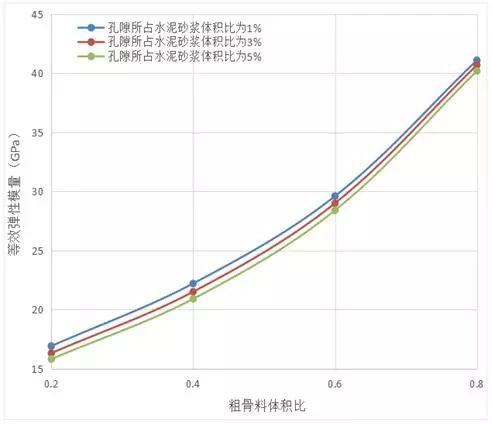
图9 孔隙所占的水泥砂浆体积比对混凝土等效弹性模量的影响
结论
(1)基于Digimat,将混凝土作为由水泥砂浆、粗骨料、界面、孔隙和微裂缝组成的多相复合材料,将含有孔隙和微裂缝的水泥砂浆作为基体,粗骨料和其包裹粗骨料的界面看作是球形颗粒,作为夹杂相,建立了混凝土模型,分别计算出等效抗压和抗拉弹性模量值。结果表明,模型预测值与试验测定值较为吻合。
(2)随着粗骨料体积比的增加混凝土的等效弹性模量成指数增加;在粗骨料体积比相同的情况下,混凝土的抗压弹性模量大于抗拉弹性模量。另外,粗骨料体积百分比在40%至70%之间时,该模型计算值与试验测定值相对误差较小,而大坝混凝土粗骨料体积百分比一般在该区间,故为预测大坝混凝土等效弹性模型提供了较为合理的参考值。
(3)各组相力学特性对混凝土的等效弹性模量均有较大影响。随着水泥砂浆弹性模量的增加混凝土等效弹性模量随之增加;随着粗骨料纵横比的增加混凝土等效弹性模量呈上升趋势;孔隙所占水泥砂浆体积比增加混凝土等效弹性模量减小。
(4)通过计算表明该模型在一定程度上能够反映出细观上的粗骨料所占不同体积百分比对混凝土抗拉和抗压弹性模量的影响以及分析了水泥砂浆弹性模量、粗骨料纵横比和孔隙所占水泥砂浆体积比对混凝土弹性模量的影响。此模型既可以用于预测混凝土的抗压和抗拉弹性模量,也能优化混凝土的材料性能。




