岩石边坡平面滑动稳定性分析---带有拉伸裂缝(with tension crack)
1 引言
在《岩石边坡平面滑动(Planar Sliding)稳定性分析》一文中,使用RocPlane演示了一个没有拉伸裂缝的例子, 本文描述一个带有拉伸裂缝的平面滑动稳定性分析例子. 此外, 简要讨论了敏感性分析方法[课程作业: 用EXCEL编写无拉伸裂缝和有拉伸裂缝的边坡平面滑动分析过程, 计算安全系数, 不考虑地震力和水压力作用]
2 求解过程
问题的几何形状如下图所示。
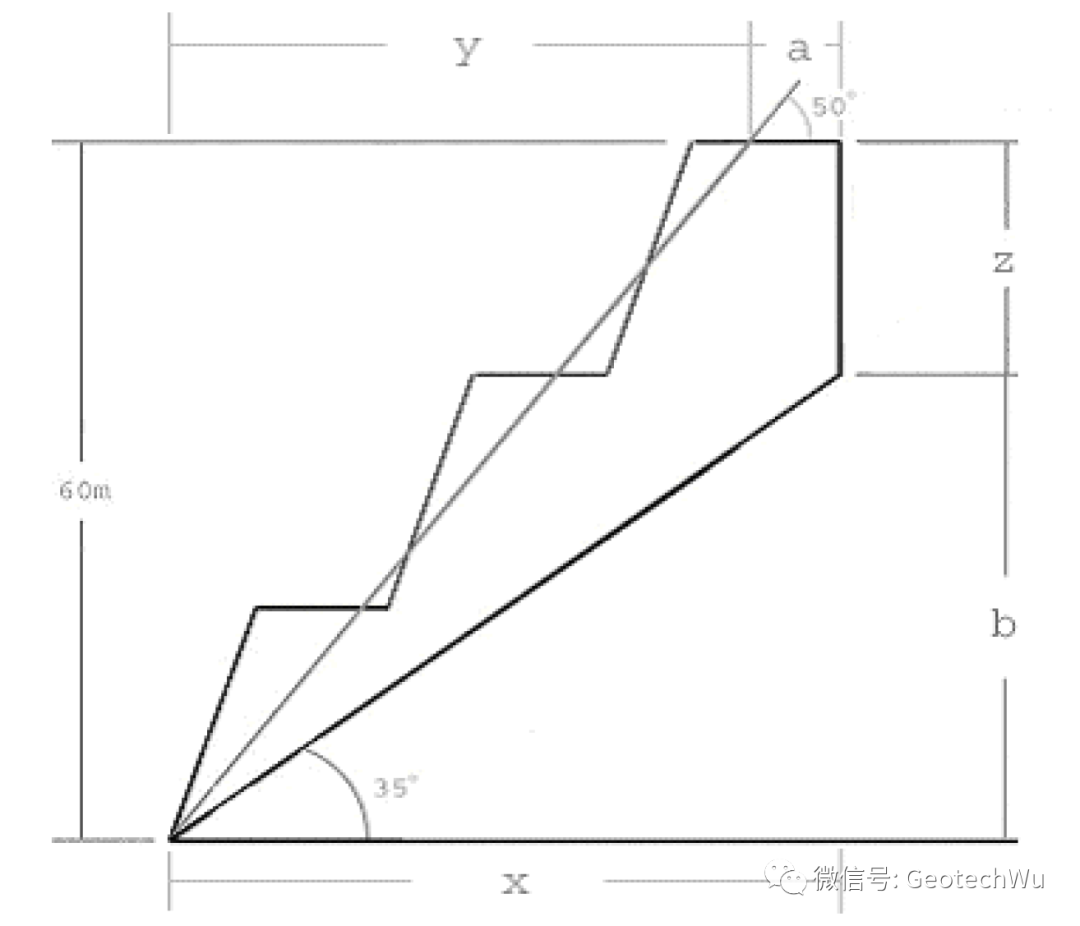
首先需要手工计算出边坡顶部与裂缝之间的距离a. 通过简单的几何运算, 可得到a=15.3357m.

(1) 输入边坡的几何形状,边坡角50,高度60,岩石密度2.7,滑动面的角度35,坡顶的倾斜角度为0, 拉伸裂缝是垂直的, 输入90, 输入裂缝距坡顶的距离15.3357。

(2) 输入滑动面的剪切强度参数,我们选择最简单的Mohr-Coulomb破坏准则,内摩擦角取35, 粘结力取10。

(3) 输入作用在边坡滑动面上的力,在此我们考虑了水压力和地震力,水压力的计算只需输入地下水的密度即可,按照静水压力计算;地震力的计算输入地震系数即可,计算方法与《Gravity Dam: 重力式混凝土坝地震力计算》一文中使用的方法一样。

最后计算出的安全系数是1.06547.
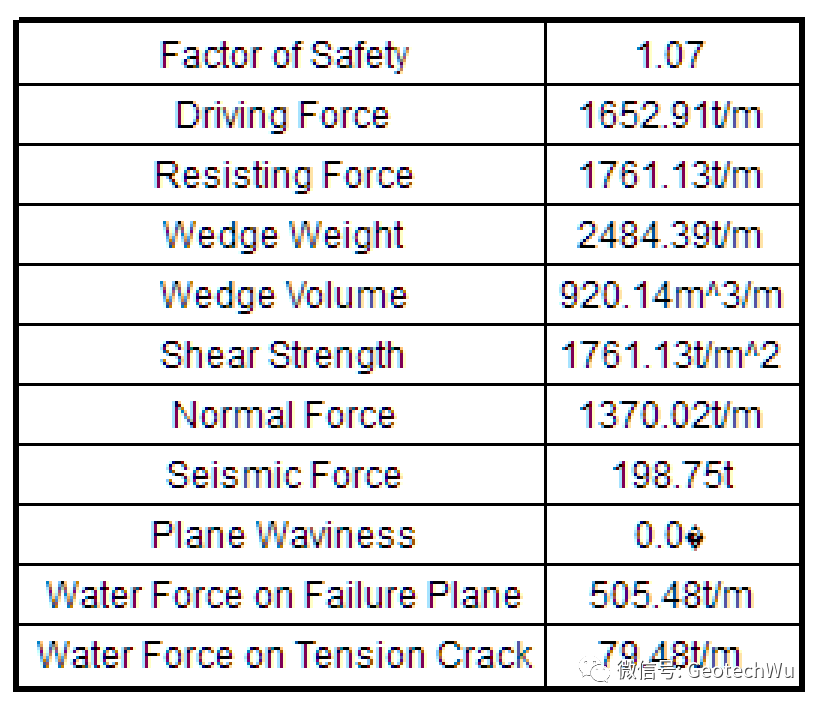
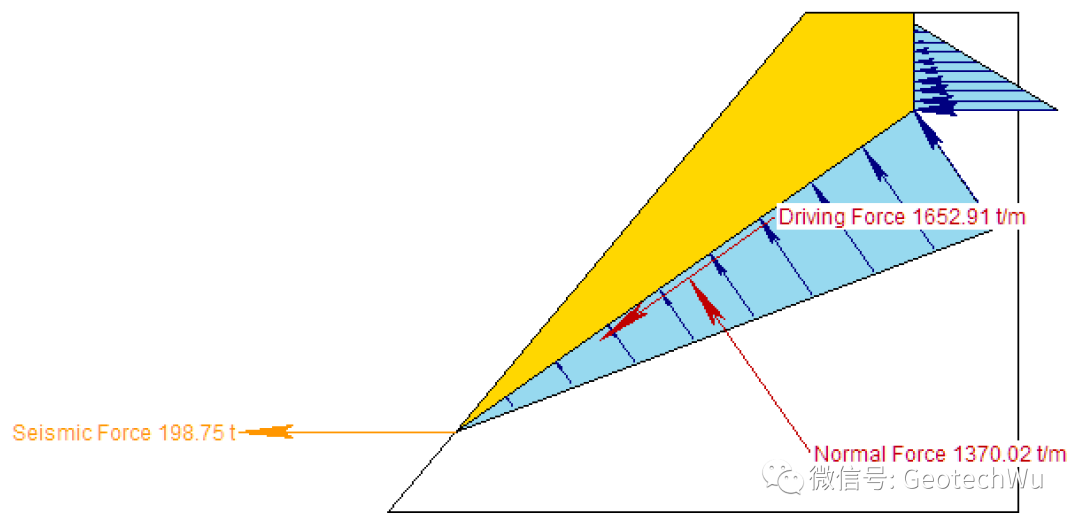
3 参数敏感性分析
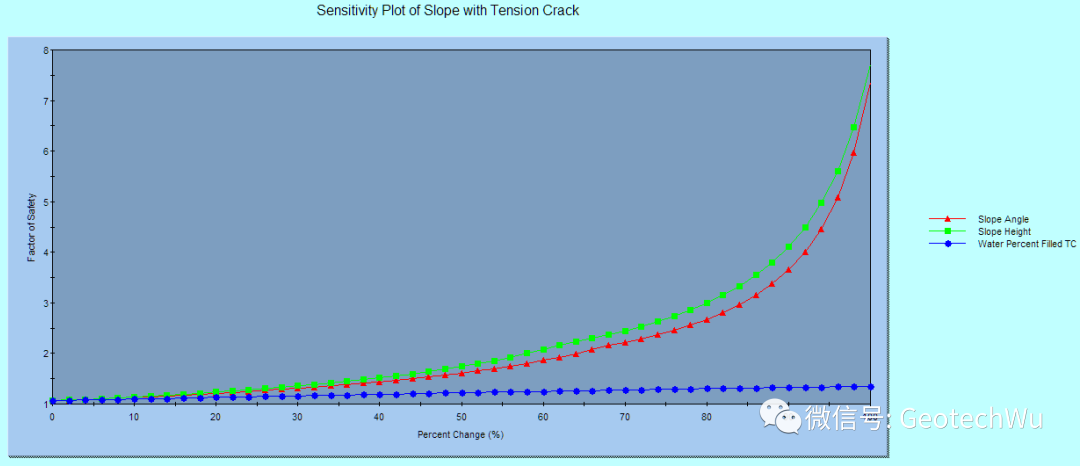
如同SLIDE一样(参看<使用BLOCK算法搜索边坡的最小滑动面>), RocPlane通过输入参数的取值范围来进行敏感性分析。在敏感性分析中,模型参数值在可能取值的范围内变化,观察不同参数值对安全系数的影响。这种做法有助于确定对滑动块稳定性影响最大的参数,并可用于比较各种治理措施的有效性。敏感性图的纵坐标是安全系数值, 横坐标是模型参数变化百分比。在敏感性图中,一个参数的曲线梯度表示该参数对安全系数的影响。上升或下降的曲线越陡,说明对安全系数的影响越大。
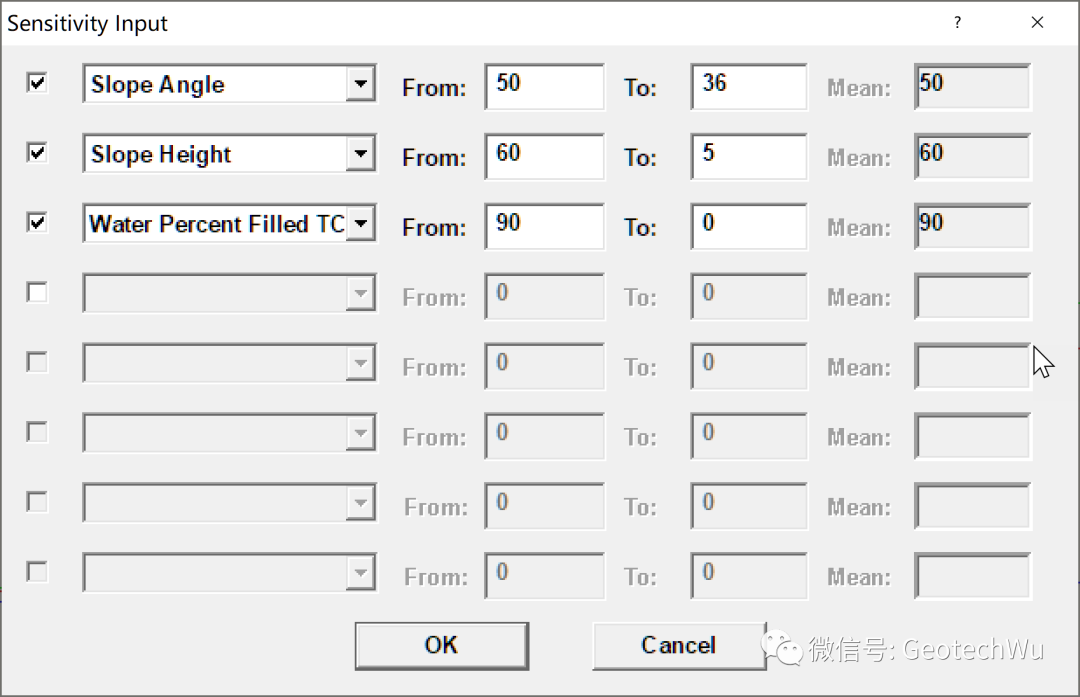
参考文献:
[1] E. Hoek, 2000, “A slope stability problem in Hong Kong”, Practical Rock Engineering, pp. 92-104.
[2] Miller, S.M. (1988). Modeling Shear Strength at Low Normal Stresses for Enhanced Rock Slope Engineering, Proc. Of 39th Highway Geology Symp, 346-356.
[3] Hoek, E. and Bray, J.W. (1981). Rock Slope Engineering, Revised 3rd edition, The Institution of Mining and Metallurgy, London.
[4] Sharma, S., Raghuvanshi, T.K. and Anbalagan, R. (1995). Plane failure analysis of rock slopes, Geotechnical and Geological Engineering, 13, 105-111.
相关文章:
岩石边坡平面滑动(Planar Sliding)稳定性分析
边坡工程---岩体边坡的破坏模式
使用BLOCK算法搜索边坡的最小滑动面
Gravity Dam: 重力式混凝土坝地震力计算边坡
UDEC: 岩体边坡阶梯状节理模拟---一个操作指导




