岩石边坡楔形体稳定性概率分析(3)---节理剪切强度的随机分布

1 引言

节理产状和节理剪切强度的随机分布是概率稳定性分析中最关键的部分. 除了节理的产状作为随机变量(<岩石边坡楔形体稳定性概率分析(Probabilistic Analysis)---Part 2>)外, 节理的剪切强度也可以定义为随机变量. Swedge内置了三种剪切强度模型: Mohr-Coulomb, Barton-Bandis 和 Power Curve. 每一种强度模型对应着不同的输入参数,  对于每一种强度模型, 都有两种定义随机变量的方法: 一种是Parameters; 另一种是Strength. 本笔记主要讨论这两种定义随机变量的方法.

2 节理剪切强度的随机变量

2.1 Parameters

如果随机变量(Random Variables)选择Parameters, 那么可以对强度准则中的每一个参数定义一种随机分布, 具体来说, 对Mohr-Coulomb准则定义c 和phi; 对Barton-Bandis准则定义JRC, JCS和phir; 对Power Curve准则定义a,b,c,d.

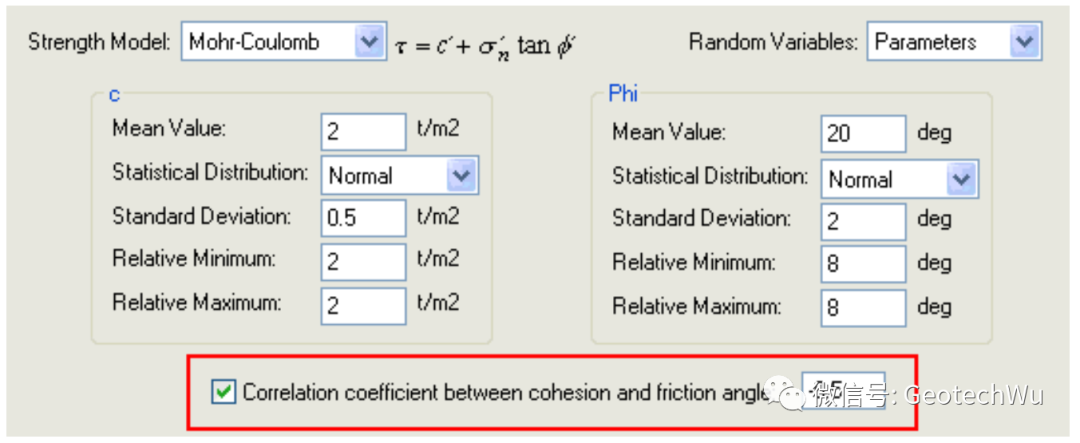
如果使用Mohr-Coulomb强度模型, 可以定义粘结力和内摩擦角之间的回归系数(Correlation Coefficient). 这个选择只有在使用Mohr-Coulomb准则时才适用,其它两种强度模型不能使用这个选项. 

2.2 Strength

如果随机变量(Random Variables)选择Strength, 那么抗剪强度(tau)将直接被定义为随机变量，而不是将强度准则中的各个参数定义为随机变量。对于一个给定的法向应力，将产生剪切强度的随机值。剪切强度的统计分布只允许采用对数正态分布(Lognormal )和Gamma分布，因为这些分布只定义为正值，因此确保随机生成的剪切强度值总是正值。剪切强度的变异系数(Coefficient of Variation) 等于标准差(standard deviation)除以平均抗剪强度。典型的变异系数值为0.15~0.35.

显然, 使用Strength选项要比使用Parameters选项简单, 输入的参数相对要少. 

3 参考文献

 [1] Meyers, A.G. and Priest S.D. (2000). Generating discontinuity orientation data for use in probabilistic models for modelling excavations in rock. In Proceedings Geo Eng 2000, November 2000.

[2] Startzman, R.A. and Wattenbarger, R.A. (1985). An improved computation procedure for risk analysis problems with unusual probability functions. Proc. symp. Soc. Petrolm Engnrs, hydrocarbon economics and evaluation, Dallas.

[3] Miller, S.M., Girard, J.M., and McHugh, E. (2000). Computer modeling of catch benches to mitigate rockfall hazards in open pit mines. Pacific Rocks 2000, Balkema, Rotterdam, pp. 539-545.

[4] Duncan, J.M. (2000). Factors of safety and reliability in geotechnical engineering. J. Geotechnical & Geoenvironmental Engineering, April, pp. 307-316.

[5] Goodman, R.E. and Shi, G. (1985). Block Theory and Its Application to Rock Engineering, Prentice-Hall Inc., New York.

[6] Hoek, E., Kaiser, P.K. and Bawden, W.F. (1995). Support of Underground Excavations in Hard Rock, A.A.Balkema, Rotterdam, Brookfield.

相关文章：

构造控制的隧道稳定性分析---Rock Wedge

岩石边坡楔形破坏稳定性分析---一个教学演示

Swedge: 岩石边坡楔形破坏稳定性分析

岩石边坡楔形体稳定性概率分析(Probabilistic Analysis)---Part 1

岩石边坡楔形体稳定性概率分析(Probabilistic Analysis)---Part 2

岩体不连续的剪切强度 | Barton-Bandis Model