教你Matlab有限元编程对悬臂梁进行受力分析-附源码及教程
导读:大家好,我是SimPC博士,主要从事工程结构抗震及减隔震研究,玻璃成型热工设备流动及传热研究,玻璃材料力学性能研究。精通有限元等数值算法的实现,有限元软件二次开发,数据处理,偏微分方程求解,优化算法,GUI界面开发等。有多项科研成果,其中SCI论文4篇,EI3篇,专利2篇。
一、问题概述
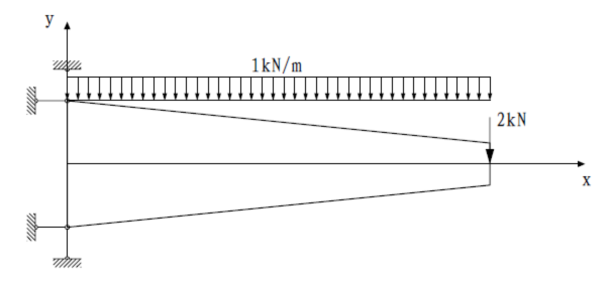
二、求解思路
几何域离散,获得标准化的单元;
通过能量原理(虚功原理或最小势能原理,获得单元刚度方程;
单元的集成(装配);
处理位移边界条件;
计算支反力;
计算单元的其他物理量(应力应变)。
节点描述
场描述
单元刚度方程。
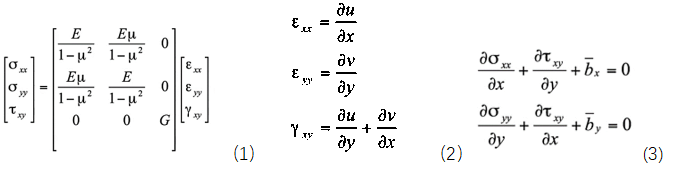
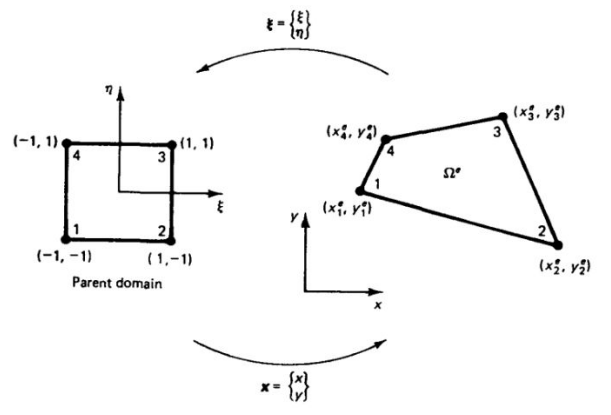
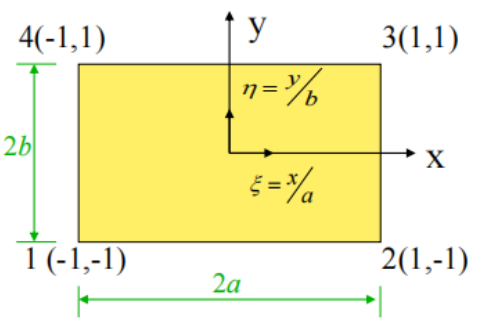
图2-1 平面四节点矩形单元的映射关系
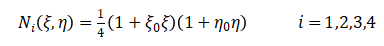 (4)
(4)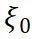 和
和 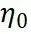 为自然坐标系下的节点坐标值。
为自然坐标系下的节点坐标值。
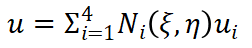 (7)
(7)function N=ShapeFun(s,t) N1=1/4*(1-s)*(1-t);N2=1/4*(1 s)*(1-t);N3=1/4*(1 s)*(1 t);N4=1/4*(1-s)*(1 t);N=[N1 0 N2 0 N3 0 N4 0;0 N1 0 N2 0 N3 0 N4];end
同理平面八节点矩形单元如图2-3所示,单元共有8个节点,16个自由度。单元的形函数定义如下:
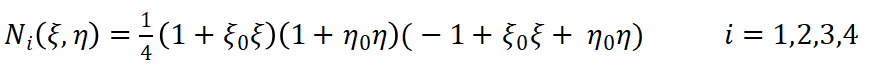 (8)
(8)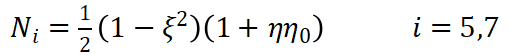 (9)
(9)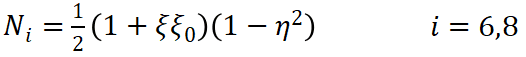 (10)
(10)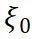 和
和 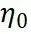 为自然坐标系下的节点坐标值。
为自然坐标系下的节点坐标值。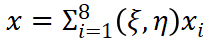 (11)
(11)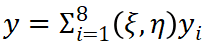 (12)
(12)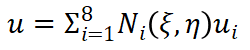 (13)
(13)function N=ShapeFun(s,t) %% 四边形八结点等参单元形函数矩阵 % 角点N1=1/4*(1-s)*(1 t)*(-s t-1); N2=1/4*(1-s)*(1-t)*(-s-t-1); N3=1/4*(1 s)*(1-t)*(s-t-1); N4=1/4*(1 s)*(1 t)*(s t-1); % 边中点 N5=1/2*(1-t^2)*(1-s); N7=1/2*(1-t^2)*(1 s); N6=1/2*(1-s^2)*(1-t); N8=1/2*(1-s^2)*(1 t); N=[N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8 0;0 N1 0 N2 0 N3 0 N4 0 N5 0 N6 0 N7 0 N8];
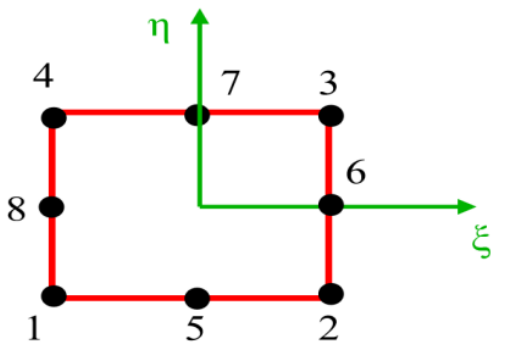
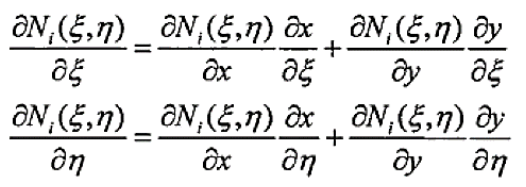 (14)
(14)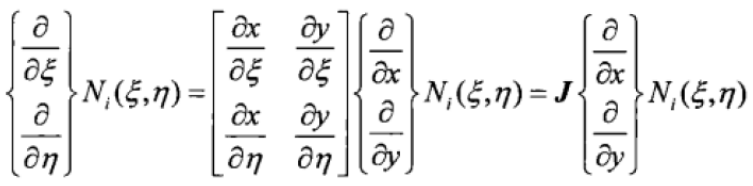 (15)
(15)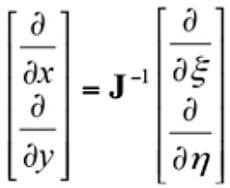 (16)
(16)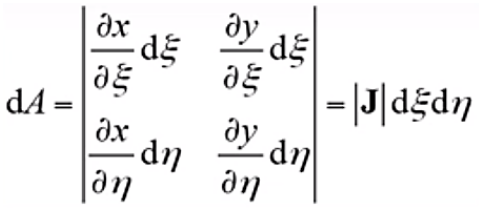 (17)
(17) (18)
(18)function J=Jacobi(ie,s,t,Elements,Nodes) ENodes = Elements(ie,:); %获取单元结点 xe = Nodes(ENodes(:),:); %获取节点坐标 x1=xe(1,1);y1=xe(1,2); x2=xe(2,1);y2=xe(2,2); x3=xe(3,1);y3=xe(3,2); x4=xe(4,1);y4=xe(4,2); J=1/4*[-(1 t) -(1-t) 1-t 1 t;1-s -(1-s) -(1 s) 1 s]*[x1 y1;x2 y2;x3 y3;x4 y4];end
function J=Jacobi(ie,kesi,yita,Elements,Nodes) ENodes = Elements(ie,:); %获取单元结点 xe = Nodes(ENodes(:),:); %获取结点坐标 x1=xe(1,1);y1=xe(1,2); x2=xe(2,1);y2=xe(2,2); x3=xe(3,1);y3=xe(3,2); x4=xe(4,1);y4=xe(4,2); J=1/4*[-(1-yita),(1-yita),(1 yita),-(1 yita);-(1-kesi),-(1 kesi),(1 kesi),(1-kesi)]*[x1 y1;x2 y2;x3 y3;x4 y4];end
为了求出上述平面四节点和八节点单元的单元刚度矩阵,需要借助能量原理(虚功原理、最小势能原理)进行推导,能量原理的推导过程大家可以参考任意一本有限元理论书籍,都会有详细的推导过程,这里就不做进一步推导讲解,直接给出物理坐标和几何坐标系下的刚度矩阵的公式
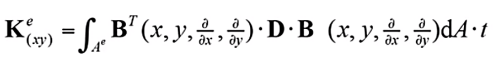 (19)
(19)
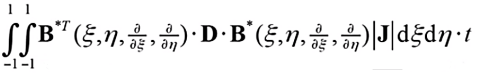 (20)
(20)
其中B矩阵为应变矩阵,如下式;D矩阵为材料刚度矩阵,如公式(1)所示,是物理方程中表征应力应变关系的矩阵。从上述刚度矩阵的表达式可以看出,自然坐标和物理坐标间要完成坐标映射、偏导映射、面积隐射三个部分,具体映射公式已在上一节的等参单元讲解中详细给出。
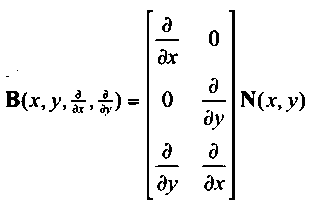 (21)
(21)
4、高斯积分
公式(20)中的单元刚度矩阵通过数值积分求得,本案例中的四节点和八节点四边形等参单元均采用2*2个积分点的高斯积分即可求得精确结果。高斯积分点的坐标具体如图所示。
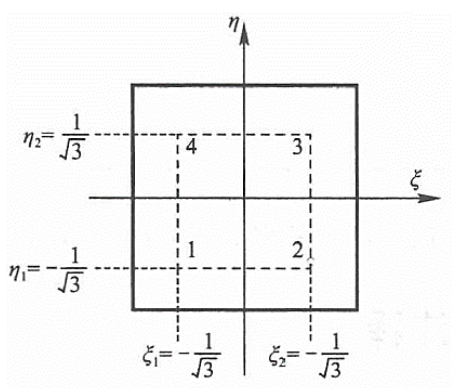
4-1 Gauss积分点示意图
公式(20)写成数值积分的形式为
 (22)
(22)
对于8节点单元实现上述数值积分的代码如下所示:
r = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点 s = [r(1) r(1) r(2) r(2)]; t = [r(2) r(1) r(1) r(2)]; % 高斯积分点坐标for i=1:4 J = Jacobi(E_ID,s(i),t(i),Elements,Nodes); % 雅可比矩阵 Nst = DiffShapeFun(s(i),t(i)); % 形函数关于自然坐标s,t求导 Nxy = zeros(8,2); for j=1:8 Nxy(j,:) = (J\Nst(j,:)')'; % 形函数关于 x,y 求导=inv(J)*Nst end Bm = [Nxy(1,1) 0 Nxy(2,1) 0 Nxy(3,1) 0 Nxy(4,1) 0 Nxy(5,1) 0 Nxy(6,1) 0 Nxy(7,1) 0 Nxy(8,1) 0; 0 Nxy(1,2) 0 Nxy(2,2) 0 Nxy(3,2) 0 Nxy(4,2) 0 Nxy(5,2) 0 Nxy(6,2) 0 Nxy(7,2) 0 Nxy(8,2); Nxy(1,2) Nxy(1,1) Nxy(2,2) Nxy(2,1) Nxy(3,2) Nxy(3,1) Nxy(4,2) Nxy(4,1) Nxy(5,2) Nxy(5,1) Nxy(6,2) Nxy(6,1) Nxy(7,2) Nxy(7,1) Nxy(8,2) Nxy(8,1)]; ke = ke det(J)*Bm'*D*Bm*Width; %数值积分 end
5、均布荷载的施加
在有限元中分布力要转为等效节点荷载,而确定等效节点荷载的方法也是通过能量原理推导得到
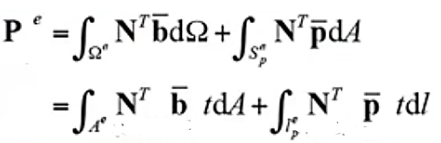 (22)
(22)
上式中,第一项代表体积力的等效荷载,第二项代表面积力的等效荷载,这个案例我们只考虑面力荷载。实现公式22的代码为
function Pe=UniLoad(ie,N_ID_p1,q0,Nodes,Elements) k=-0.625e-3; % 均布荷载值 N/mms = [-sqrt(1/3) sqrt(1/3)]; % 2*2 高斯积分点ENodes = N_ID_p1(ie,:); %获取单元结点号Pe=zeros(16,1); %生成临时单元节点力零列向量x1=Nodes(ENodes(1),1);x6=Nodes(ENodes(4),1);L16=abs(x6-x1); %单元长度for i=1:2 %用于高斯积分的求和循环 N_q=ShapeFun(s(i),1); % 4级子程序:ShapeFun(s(i),1) q_x=q0; Pe=Pe N_q'*q_x*[0;L16/2]; endend
三、Matlab有限元编程精品课
网格划分及变形结果如图3-1所示。本案例的详细视频教程和对应的matlab源码,请关注我的仿真秀官网和APP精品课程《Matlab有限元编程从入门到精通10讲》。

图3-1 梁变形结果
此外,为帮助大家更好的入门学习Matlab有限元编程分析能力,欢迎大家直接在附件下载。如果遇到问题请在文章下方留言或者联系平台小助手。
我的Matlab有限元编程精品课
本课程为matlab有限元编程专题课,课程主要以案例的形式进行讲解,中间会穿插案例中所涉及到的有限元基本理论,案例不局限于力学问题的有限元求解,还会涉及传热学、电学等问题的有限元求解。
因为固体力学领域我最熟悉,所以我们从固体力学开始,所涉及的单元有杆单元,梁单元,平面三角形单元,薄板单元,厚板单元,四面体实体单元等等,力学问题有静力学问题,也有动力学问题,后期还会涉及材料非线性、几何非线性、接触非线性等非线性问题,内容丰富,不断更新完善。
此外,笔者为所有订阅用户提供知识圈答疑服务和VIP用户交流群。并附赠课程相关资料等(平台支持自行开具电子发票)。
快速获得各典型有限元案例的Matlab代码; 学习并掌握有限元基础理论; 掌握Matlab编程实现有限元算法的流程; 掌握多种有限元单元的基本理论Matlab编程实现过程; 掌握静力学、动力学、材料非线性、几何非线性、接触非线性问题的Matlab编程实现; 为订阅用户提供知识圈答疑服务,并建立VIP用户交流群,后续可根据订阅用户需求进行加餐直播。此外还提供课程对应的学习资料模型一份。
理工科院校学生和教师;
学习型仿真设计工程师;
Matlab有限元编程兴趣爱好者和应用者。








