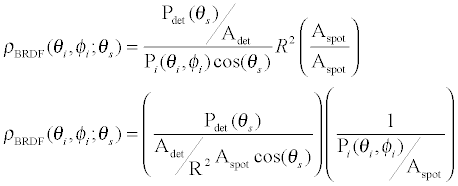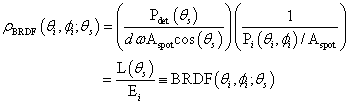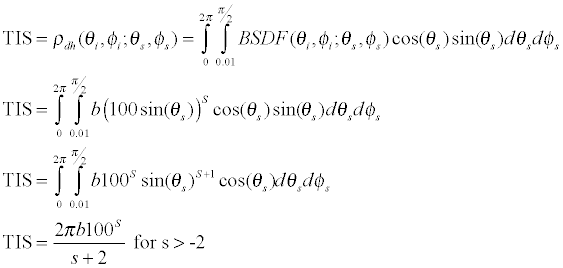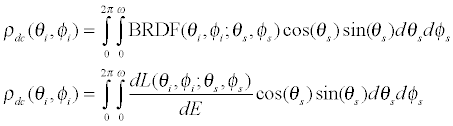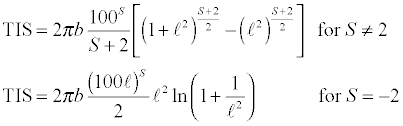ASAP杂散光分析中的散射模型
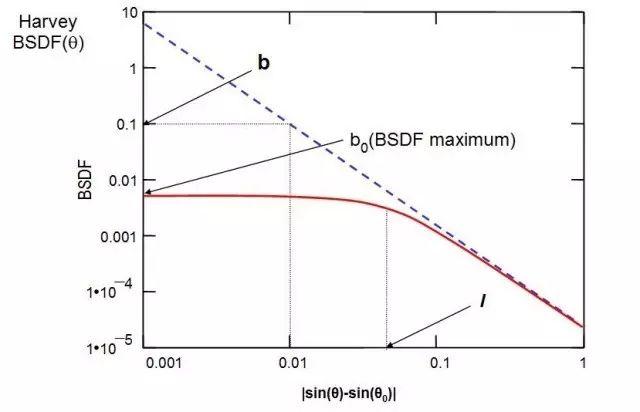
根据应用的方向, 或根据散射计算过程中所产生的散射光线的数目, 可以把 ASAP 的散射模拟方法分成好几类。 在某些应用中, 入射光线打在散射表面上时, ASAP 会根据某一特定散射函数 (scat-tering function) 对光线的传播方向进行微扰, 使之偏离镜面路径 (specular path), 而不产生新的散射光线。 在其它的应用中, ASAP 会产生一条或多条的光线以模拟散射光。在ASAP 中, 可以用 LEVEL 指令来控制在散射接口上产生的散射光线能否继续被其他接口散射, 或每一根光线可以被散射的次数。ASAP 亦会根据用户在界面的反射及透射方向上定义的不同散射模型来产生散射光线。在 ASAP 中, SCATTER RANDOM 指令是用来仿真朗伯(Lambertian)表面。朗伯散射表面的散射亮度为常数而与光线的入射角度无关, 其散射光强度则根据散射光线与该表面法线方向夹角的余弦值而改变。 这方法常用来模拟简单的扩散片(diffuser)。当一条入射光线打在以此指令定义的散射面上时, ASAP 将产生多条的额外光线以模拟朗伯散射表面 。 换句话说, 这方法对应的是`一条光线进, 多条光线出'的散射模拟方法。 这些光线是被散射到一个半球形的区域内, 每一根光线携带相同的光通量 (flux)。ASAP 采用一个名为光线密度 (ray-density method)的算法来产生这朗伯散射光线的空间分布模式: 当入射光线是在散射表面的法线方向附近, ASAP 在单位立体角度内产生的光线数目比较多; 当光线是掠入射 (grazing incident)时, 将产生较少的散射光线。在使用 ROUGHNESS MODEL 指令时, ASAP 会随机改变与入射光线相交处的表面法线方向, 从而改变反射及透射光线的方向来模拟粗糙表面。ASAP 会首先根据用户定义的射散模型在内部产生一个数学统计模型 -- 表面斜率统计(surface slope statistics)。 ASAP 以此统计模型为前述表面法线方向的随机取样基础。当光线为正向入射于散射表面时, 此表面斜率统计模型的数学定义会使得发出来的散射光线分布与原来定义的散射模型恰好相符。要注意的是, 当光线是非正向入射时, ASAP 仍然采用同一表面斜率统计模型进行计算。使用此方法时, 没有产生新的散射光线: 对每一根入射光线, ASAP 通过对传播方向的改变而将之转化成散射光线。这方法常用在照明设计中对粗糙表面的模拟。使用 SCATTER MODEL 指令时, ASAP 会根据用户所定义的散射模型, 把光线散射到指定的面积或立体角内。 类似于SCATTER RANDOM指令, 对应每一条入射光线, SCATTER MODEL 指令会产生多条射散光线; 然而, SCATTER MODEL 产生的光线各携带不同的光通量, 其大小取决于下列因素: 散射函数, 散射光束传播的面积, 以及所对应的立体角。换言之, ASAP根据所定义的散射函数对各光线进行加权运算。在使用SCATTER MODEL 及ROUGHNESS MODEL 指令时, 用户必须先在 ASAP 中定义散射模型以产生散射函数。 SCATTER BSDF 或 SCATTER RMS (表面散射) SCATTER BSDF 及 SCATTER RMS 指令是用来仿真由成像系统内光学组件产生的视场**散。对应于每一根打在散射表面上的入射光线, ASAP 会产生一根散射光线; 其传播方向将非常接近于入射光线的镜向方向 (specular direction)。 MEDIA... SCATTER... (体散射) 在 ASAP 中, 可以使用 MEDIA 指令来仿真体散射 (volume scattering)。根据用户定义的体散射模型, ASAP 使用蒙地卡罗(Monte-Carlo)算法对在体散射介质内传播的光线进行微扰。如果用户定义的是非均匀体散射模型(inhomogenous volume scatter model), 则其散射性质会根据光线在介质中的三维空间位置而改变。散射光线对散射角度的分布则可以定义为各向同性, 例如在米氏散射(Mie scattering)或 Henyey-Greenstein 散射的情形; 在其它情况, 使用者可以自定函数来描述。进行散射分析吋, 往往需要定义散射模型。ASAP 会根据用户输入的散射数据, 建立标准的几何散射函数 -- 双向散射分布函数 (Bidirectional Scattering Distribution Function, BSDF), 来描述散射模型。BSDF测量乃是描述表面散射的业界标准。当光线打在理想的光滑表面时, 光线会进行纯粹的镜面反射及透射。当这表面是理想的漫射 (dif-fuse)表面吋, 将会发生纯粹的漫射反射及透射。在现实中, 没有表面是完全的光滑或漫散, 而是介乎两者之间并呈现散射的性质。 此时, 便需要使用BSDF函数以详尽地描述散射行为。为了简单起见, 以下只针对反射的情况讨论; 透射的情况将会类似。双向反射分布函数常用来描述反射散射的一般特性。它是入射角度及散射角度的函数(因而被称为双向, bidirectional)。程序1 显示了与波长无关的BRDF函数的定义:E 是入射光照度(incident irradiance, 单位面积上的光功率); L 是散射亮度(scatter radiance) 。 BRDF 的单位是空间立体角(solid angle)或球面度(steradian)的倒数。极角(polar angle)通常从表面法线量起。方位角(azimuth angle)是从某一参考平面量起; 通常这平面被选定为光线的入射面(plane of incidence)。 在 ASAP 中, 常以 YZ 平面来代表这入射面。 在以下的讨论中, 我们便沿用此设定, 以YZ平面作为入射面。如果讨论的是各向同性 (isotropic)的散射表面, 其 BRDF 变成只有三个变数的函数: 入射极角, 入射方位角, 反射极角与散射极角的差值。换句话说, 各向同性表面的反射散射, 对应于入射面及散射表面的法线方向呈现对称性 -- 当散射表面绕其法线转动时, 其反射散射性质不变。同理, 各向同性表面的透射性质亦呈现相同行为。拉丝面或金刚石车削表面为各向异性散射表面(anisotropic scattering surface), 其散射性质对应入射面及散射表面的法线方向不具有转动对称性。程序 1 是BRDF 函数的数学定义, 可以用来描述某一表面的反射散射性质。但是它是怎样推导出来的呢? 当量测散射功率时, 其数值会与量测仪器的几何形状大小有关; 但是我们真正想要的散射量测却应该只与散射表面的性质相关。让我们来考虑下述的情况: 我们首先搭建起一个探测器来测量从一个各向同性的表面反射的功率; 这探测器相对于散射表面法线的角度(散射角)可以改变。理论上, 我们可以用在不同入射及散射角上量测的功率与入射功率的比值作为该表面散射性质的一个度量。但是, 探测器的大小会影响功率读值的大小, 因而影响散射性质的计算。很自然地我们便会想到应该先把探测器量到的功率除以探测器的面积, 再来进行散射度量的计算。这样, 散射表面的反射率便可以写成如下(程序 2):接下来, 我们需要考虑探测器与光源的距离, 因为探测器上的功率与此距离成平方反比的关系。而且, 因为探测器表面不一定平行于反射表面, 我们真正需要考虑的是探测器的投影面积 (projected area); 因此, 我们便需要引进一个余弦因子(cosine factor)。经过这些修改后, 上式便可以改写成:接下来, 我们对分子及分母同时乘上样品表面上入射光斑的大小(spot size): 在上式的第一个括号中的分母处的分数表达式事实上就是探测器对样品表面上的光斑中点所张的立体角。当把探测器上的功率除以此立体角与光斑投影面积的乘积, 对应的便是该表面的辐射亮度; 而入射功率除以光斑的面积便是入射在表面上的辐照度(irradiance)。因此, 上式便可以改写如下:由此我们便可以得到下述结论: BRDF 是表面辐射亮度除以表面光照度。BRDF是描述反射散射的一个很重要的物理量。这是因为辐射亮度本身很重要: 其他的辐射度的物理量(例如, 光强度及光照度)均可以通过对辐射亮度进行积分运算而推导。作为一个例子, 我们可以探讨 BRDF 与漫反射率(diffusive reflectivity, 亦称为半球方向反射率, directional hemispherical reflectivity)的关系。由于此时考虑的是被反射到一个半球空间内的功率, 作运算时, 我们便需要把 BRDF 函数对整个半球所张的立体角作积分:这也就是全积分散射(Total Integrated Scatter, TIS)的定义。TIS 亦可以被定义成: 从表面散射到整个半球空间内的功率除以入射在该表面上的功率。 很明显地, TIS 将会是入射光线的极角及方位角的函数。如果是各向同性的表面, 则BRDF 将会只是极角的函数。朗伯表面的辐射亮度(L)是常数, 则上式可以写成:因此, 朗伯反射表面的BRDF乃是漫反射率除以 π。事实上, 上述结果可以通过朗伯表面的出射度(exitance)定义来推导: 因为朗伯表面的出射度是 πL, 直接应用漫反射率的定义便可推得上式。如果所讨论的表面是所谓的镜面表面(specular surface), 其散射性质通常可以用哈维(Harvey)定律来描述。哈维散射模型常用来描述光滑打磨表面的散射性质; 通常需要两个或以上的参数来定义此模型。其 BSDF 函数的极大值通常发生在镜向方向上。哈维(Harvey)发现, 如果把这类表面的 BSDF 函数, 在某特定座标内, 对入射角度描图, 将会观察到一种不变关系(invariant relationship):如果我们先对光线的散射角度及反射角度(或透射角度)取正弦值, 计算其差值后取对数, 以此作为水平轴对哈维 BSDF 函数的对数值描图, 其函数图形不会因入射角度不同而改变。当把哈维散射表面的BSDF函数在上述的对数-对数空间中描图时, 都会呈现直线图形; 而且, 不同入射角度的图形会重叠在一起。描述基本哈维模型的两个参数便分别是此直线的斜率(slope)及截距(intercept)。由于只需要两个参数来描述此散射函数, 这大大减少了该散射模型的复杂度。很多经过打磨的表面都显示哈维散射性质。图2. 此图显示了两类哈维散射模型: 实线是包含肩参数(shoulder parameter, l)的模型; 虚线则不包含肩参数。对应于各向同性的表面, 不包含肩参数(shoulder parameter) 的基本哈维模型可以写成如下式所示(程序 8) :b 是在横轴座标 0.01处的 BSDF。把散射角度及反射(或透射)角度取正弦, 求其差值后取对数, 再以此作为横轴对 BSDF 的对数值描图, 所得的直线的斜率便是式中的指数(exponent), S。把这程序对整个半球作积分便可以得到全积分散射, 如下式所示:值得注意的是, 在上式中, 积分的角度是从 0.01 到 π/2 弧度, 而不是整个半球; 这是有其物理及历史的依据。参数 b 是在0.01 弧度处的 BSDF 值(基本上就是该 BSDF 直线在 Y 轴上的截距)。从实践应用的角度而言, BSDF曲线一般会以此角度为量测的极限: 任何小于此角度的量测皆视为不可靠, 因为衍射的效应使得入射光束有一定的大小, 从而影响量测结果; 这就是所谓的仪器误差(译注: 原文用的是instrument signature, 直接翻译将是仪器签章, 而不是仪器误差。这虽然是正确的翻译, 却是太挠口, 而且辞不达义。但是我们觉得有必要向读者提点, 因为instrument signa-ture 是在英文的杂光文献中常用到的词汇)。从理论的角度而言, 没有任何模型可以准确地描述在反射或透射方向 0.01 弧度以内的 BSDF。当光线为正向入射时, 用哈维模型算出来的BSDF 值会是无限。利用前面介绍的 BSDF 关系式, 可以显示在镜向方向附近, BRDF 函数对应的极大反射率可以大于 1 。如果只考虑镜面反射的情况, 大于 1 的反射率是颇为使人困惑的; 但从数学的角度而言, 这却是 BSDF函数定义的自然结果。这现像可以从锥形方向反射率(directional conical reflectivity)来解释。锥形方向反射率与半球方向反射率非常相似, 差别之处只是在进行计算时, 该积分只是针对某一锥形立体角, 而不是整个半球。因此,锥形方向反射率可以表达如下式所示:下式所示则是差分锥形方向反射率(differential directional conical reflectivity):现在, 让我们来考虑一束近乎准直的光线打在一个光滑平面上的情况。因为反射光束仍然近乎准直, 上式分母中的投影立体角将非常接近零。在此极限下, BRDF值将为无穹大, 如下式所示:在现实中, 当考虑光滑平面在镜向方向附近的BRDF时, 其大小虽然不会是无限, 但却可以是很大。从理论的角度, 这现像是绝对可以存在的; 因此, 从应用而言, 我们便需要设法在散射模型的定义中阻止此情况的发生。例如, 在ASAP的哈维BSDF模型中, 为了避免其数值在镜向方向上变成无限大, 我们引进了一个肩下降参数(shoulder roll-off parameter), 如下式所示:b 是在0.01 弧度处的BSDF; b0 是当 θ = 0 时的BSDF; l是肩参数, 其单位为弧度。散射模型的BSDF值在肩参数处开始趋向一个常数。跟前面一样, 我们可以把这改进过的BSDF函数对半球积分以计算TIS。下式所示为正向入射时的积分结果:在进行杂光分析时, 一个很重要但却常被忽视的步骤乃是使用者必须依据量测数据发展一个合理而且良好的散射模型。虽然ASAP提供了从简单到复杂的模型来仿真各种不同散射的BSDF数据, 但你必须根据你的应用项目而决定适合的模型。举例而言, ASAP可以模拟描述理想漫射的简单朗伯模型; 此模型只需要单一输入参数: 半球反射率(hemispherical reflectivity)。 但是ASAP也可以仿真更复杂的模型; 这些模型往往需要用到光线的入射角度, 散射角度, 以及BSDF量测值作为输入参数以进行拟合或内插而产生散射模型。ASAP散射模型皆服从互换定律(law of reciprocity)。它的含义是: 如果把入射方向与散射方向交换, 所对应的BSDF值相同。因此, 各向同性表面的BSDF函数对镜向方向及散射方向具有对称性。LAMBERTIAN - 常用来描述单纯的漫射; 只需要单一参数: 半球反射率或透射率。HARVEY - 当散射光线是集中在光滑表面的镜向方向的附近时, 哈维是常用的模型。此模型用到的标准参数主要是由BSDF值与角度在对数-对数座标的描图而决定; 这包括了描图线段在纵轴的截距(参考BSDF值), 以及该线段的斜率; 有时还会加上肩参数。此模型亦会随波长而缩放。POLYNOMIAL/TRINOMIAL/BINOMIAL - 这些是极为有用的指令。它们可以用来定义一般性的各向同性表面散射模型(例如, 涂漆表面)。通常可以把这些散射模型定义为某些自由变化的参数的多项式。使用者可以直接输入多项式的系数, 或让电脑对量测的BSDF 数据进行拟合以决定这些系数。NONLINEAR - 这模型是哈维模型(狭窄的散射峰)及Thong 模型(对应于较宽广的散射分布)的组合。它可以用来描述光滑或粗糙的表面。这模型的系数亦可以直接输入或对BSDF数据进行拟合而决定。USERBSDF - 这指令本身事实上就是一个ASAP内定的宏语(macro)。它用一个三维函数来描述用户自定的散射模型。这函数所在的座标并不是一般的三维空间, 乃是所谓的各向同性表面对称变数(isotropic surface symmetry variables)空间。RMS - 主要用来模拟具有轻度起伏不平但仍然光滑的表面。PHYSICAL - 一个详尽的反射散射模型; 什至可以用来模拟在粗糙表面上掠射光线的散射。VCAVITY - 这指令产生一组散乱分布的V型空腔来模拟粗糙表面。由于这些空腔是被定义成几何形状, 传播中的光线会被它们遮挡或产生多次反射。PARTICLES - 这指令让用户仿真在表面上散乱分布的粒子对入射光线的散射。其散射行为乃是通过Henyey-Greenstein 模型或米氏模型来计算。BSDFDATA - ASAP 根据用户输入的BSDF量测数据(对应于不同的入射及散射角度)进行内插运算(interpolation)以产生散射模型。使用者可以用 SUM 揩令把前述的散射模型结合以产生新的模型; 由此产生的模型亦可以接续用在另一个 SUM 指令中。ASAP亦提供一个BSDF数据拟合接口 (BSDF fitting utility) 帮助用户根据量测数据产生HAR-VEY 或 POLYNOMIAL 模型。 见图3。图 3. BSDF 拟合界面及其产生的ASAP 档案。· ASTM (American Society for Testing and Materials) 格式; 参考文獻, "Standard Prac-tice for Angle Resolved Optical Scatter Measurements on Specular or Diffuse Sur- faces".· ASCII 格式; 例如由 Schmitt Industries 的散射测量仪所产生的数据。· ASAP BSDF 拟合介面产生的 HARVEY 模型数据 (适用于ASAP 6.6 或以后的版本)。在进行哈维模型拟合时, 用户可以用鼠标直接在 BSDF 图线上点选指定哈维模型的参数, 或是使用自动拟合让 ASAP 自行决定。 HARVEY 拟合过程亦让用户把两个哈维模型结合起来。在进行 POLNOMIAL 拟合时, 用户需要输入所需的系数。不管是哪种拟合过程, ASAP都会把对应的模型定义打印出来让用户直接放到他们的ASAP 档案。 ASAP亦提供一个各向同性表面的散射数据库;这库内的散射模型都是对量测数据进行拟合而产生。如前所述, 从拉丝面或金刚石车削表面等各向异性表面散射的光线, 相对于光线入射面及散射表面的法线方向, 没有转动对称性。因此, 在对该等表面定义散射模型时, 模型的座向便变得很重要; 这方向往往是以一个额外的坐标轴参数来指定。在以下列示的模型中, 除了第一个模型以外, 其它的都有相对应的各向同性模型。VANES - 用以模拟平行于某一方向的挡光片(vane)端缘轨迹的散射。HARVEY - 对应于各向同性的哈维模型; 此模型具有椭圆对称性。NONLINEAR - 对应于各向同性的NONLINEAR 模型。USERBSDF - 对应于各向同性的USERBSDF 模型。BSDFDATA - 对应于各向同性的BSDFDATA 模型。图4列示了, 当入射光角度为30° 时, 由LAMBERTIAN, 各向异性, 及各向同性哈维模型仿真出来的散射光。图4. LAMBERTIAN, 各向异性及各向同性哈维模型在30°入射时的散射。在图5中, LAMBERTIAN, 各向异性, 及各向同性的哈维模型分别被定义在一个圆管的不同部位上; 光源乃是在圆管的正上方。图5. 从圆管表面的LAMBERTIAN, 各向异性, 及各向同性哈维模型的散射。以上的插图是由RENDER 指令所产生; 此指令可以用来对包含有散射物体的场景产生逼真的视像效果。图6显示了从车胎 (朗伯表面)及轮毂 (各向异性表面) 的散射。这例子进一步显示了ASAP对散射的强大仿真功能。所有这些各向异性的散射模型可以通过SUM指令结合产生新的模型; 而这模型亦可以重复使用在别的SUM指令中。但是要记得的是, 所有这些各向异性模型必须具有相同的方向特性。在ASAP中, 体散射的模拟跟表面散射的很不一样。在体散射中, 光线在散射介质中传播的路径会依据散射函数而改变, 但却不会在该介质中产生额外的散射光线。ASAPA根据蒙地卡罗算法, 对在体散射介质内传播的光线路径进行微扰以模拟体散射常见的随机漫步。这蒙地卡罗算法, 加上 ASAP中的VOXEL 指令 (用以定义体像素, volume pixel element), 可以让用户分析该区域内的积分通量 (fluence)分布; 见图7。图7. 在ASAP中进行体散射及体积内积分通量分布的分析。VOLUME MIE - 根据米氏模型来仿真在一定体积内分布的粒子对入射光的散射。VOLUME - 以Henyey-Greenstein 方法来模拟体散射介质对光线的散射。 表面散射模拟的重要区域采样 (importance area sampling) 方法
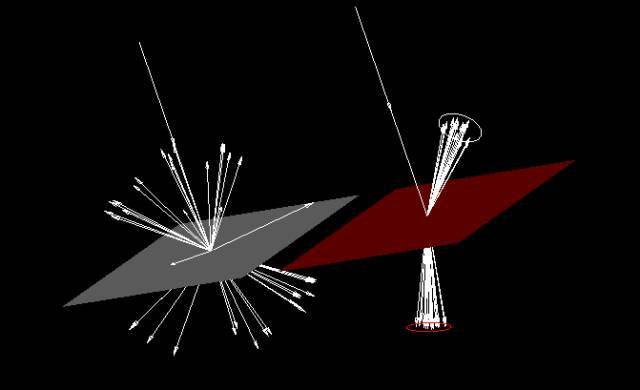
表面散射模拟的重要区域采样 (importance area sampling) 方法 如果你需要考虑的传播光线是集中在一个窄小的立体角内, 或是只打在空间中某一细小的面积或区域内, 那么, 让光线散射到整个半球空间, 并不是十分有效的散射模拟方法。幸运地, ASAP给用户提供了一个非常有用的功能来指定在哪个立体角或面积范围内的散射光线会被产生; 这就是 TOWARDS 指令的功能: 它让ASAP只在用户所关心的区域 (例如, 光瞳位置)内产生散射光线, 从而节省了模拟时间, 使整个光线追迹的过程更为有效。图 8 显示了光线如何被散射到指定的重要区域内。重要区域采样法是杂光分析软件中不可或缺的功能。图8. TOWARDS 指令的设定对散射光线的产生的效应。强劲的散射仿真功能, 加上宏语的灵活性, ASAP 可以计算打在探测器上的杂光强度, 以及其他的辐射物理量: 例如光照度, 光强度, 辐射亮度, 以及点源透过率(point source transmission, PST) 。PST 亦被称为归一化的探测辐射照度(normalized detector irradiance, NDI), 或归一化的点源辐射照度透过率(point source normalized irradiance transmission, PSNIT)。 PST 基本上就是点光源在入瞳(entrance pupil)所产生的光照度与对应的杂光在探测器上的光照度的比值(信噪比), 它是视场角(field angle)的函数; 由于它是由探测器上的光照度决定, 它的数值在探测器表面的不同位置上会改变; 可以用 ASAP 中的 SPOTS POSITION 指令来计算。PST 常用在卫星成像光学系统中量度杂光的严重性。由于ASAP 忠实地记录每根光线的产生以及在系统中传播的过程, 这使得PST的计算可以实现。纵使散射光线及讯号光线可能同时打在探测器上, 用户可以使用 SELECT 指令把杂光分离出来进行绘图或数值运算。再者, ASAP 中的 PATHS 指令让用户把杂光分为不同的路径, 进而可以选择对某一特定路径进行数值分析或描图以观察杂光的来源。细节请参阅以下在鬼像分析中的讨论。
如果你需要考虑的传播光线是集中在一个窄小的立体角内, 或是只打在空间中某一细小的面积或区域内, 那么, 让光线散射到整个半球空间, 并不是十分有效的散射模拟方法。幸运地, ASAP给用户提供了一个非常有用的功能来指定在哪个立体角或面积范围内的散射光线会被产生; 这就是 TOWARDS 指令的功能: 它让ASAP只在用户所关心的区域 (例如, 光瞳位置)内产生散射光线, 从而节省了模拟时间, 使整个光线追迹的过程更为有效。图 8 显示了光线如何被散射到指定的重要区域内。重要区域采样法是杂光分析软件中不可或缺的功能。图8. TOWARDS 指令的设定对散射光线的产生的效应。强劲的散射仿真功能, 加上宏语的灵活性, ASAP 可以计算打在探测器上的杂光强度, 以及其他的辐射物理量: 例如光照度, 光强度, 辐射亮度, 以及点源透过率(point source transmission, PST) 。PST 亦被称为归一化的探测辐射照度(normalized detector irradiance, NDI), 或归一化的点源辐射照度透过率(point source normalized irradiance transmission, PSNIT)。 PST 基本上就是点光源在入瞳(entrance pupil)所产生的光照度与对应的杂光在探测器上的光照度的比值(信噪比), 它是视场角(field angle)的函数; 由于它是由探测器上的光照度决定, 它的数值在探测器表面的不同位置上会改变; 可以用 ASAP 中的 SPOTS POSITION 指令来计算。PST 常用在卫星成像光学系统中量度杂光的严重性。由于ASAP 忠实地记录每根光线的产生以及在系统中传播的过程, 这使得PST的计算可以实现。纵使散射光线及讯号光线可能同时打在探测器上, 用户可以使用 SELECT 指令把杂光分离出来进行绘图或数值运算。再者, ASAP 中的 PATHS 指令让用户把杂光分为不同的路径, 进而可以选择对某一特定路径进行数值分析或描图以观察杂光的来源。细节请参阅以下在鬼像分析中的讨论。 著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2022-11-11
最近编辑:2年前