在进行有限元分析时，如何评判网格的质量？

理论上讲，模型中使用的单元越多，结果就越接近真实结果。然而，我们不可能去分析无限多的单元，一方面是为了节省计算资源；另一方面网格划分也是一种艺术，它能体现出大神和新手的区别。所以在计算时，我们需要找到计算的规模（网格数量）和计算的准确性之间的平衡。建议在此之前，我们不妨问自己如下问题： 

非线性分析往往比线性分析有更严格的网格要求。例如滑动接触问题可能需要一个更精细的网格来捕捉变化的状态行为；高级材料，如塑性、超弹性等，通常需要更精细的网格来捕捉大应变梯度；大变形分析需要更精细的网格来适应分析过程中形状的大变化。
       我关注的区域在哪里？

  

 如果事先知道关注区域在哪里，与其细化整体网格，不如将单元集中在关注的区域，粗网格通常足够用于力传递，可以用于不需要应力信息的区域。如果事先不知道关注的区域，可先进行粗网格分析，确定后续分析中需要细化的区域。  

小特征将会如何影响结果？

 

小孔、圆角、凸角、窄边都将自动生成一个非常精细、局部化的网格。我们需要评估这些特性是否会影响分析：它是否在关键区域？它会影响加载路径吗？这些需要用户在求解精度和时间中做出权衡。

我需要一个什么样的结果？

 

对于线性分析，精确的位移结果不需要像应力结果那样精细的网格——如果分析是为了确保位移不会太大，那么可以使用较粗的网格，如果分析需要评估结构的应力，在关键的区域需要加密网格。 

我在使用什么样的单元？

 

有些单元在弯曲时比较“刚”，需要在零件的厚度上加密网格来正确地捕捉弯曲行为。这类问题通常被称为“锁定”，原则上有中间节点的单元（二次单元）比线性单元更不容易被锁定，但如果弯曲非常显著，即使使用带中节点的单元，也建议厚度上大于一个单元。此外，某些单元的形状对变形更敏感。例如，一个六面体单元可以拉长，但仍然提供良好的结果。然而，一个四面体单元在一个方向上伸长时会产生小角度，这可能会提供不那么精确的结果。

在网格生成之后，用户可以通过观察单元的质量来评估网格。单元的质量是非常主观的——一套网格在一组边界条件和载荷下给出好的结果，在另一组边界条件和载荷下可能给出糟糕的结果。然而，它依然不失为一个有用的工具来大致了解网格的质量好坏。Simulation软件中有不同的网格质量度量，每个度量评估单元的不同特征，能够以不同的方式影响结果。下面列出了一些常见的质量度量标准：

高宽比。是单元的最长边与最短边的比值。理想的单元具有1的长宽比，但如果有一些大高宽比的网格是否会影响计算精度呢？如果实在不好划分网格一方面需要查看这样的网格分布的位置，另外一方面要看占总体网格的比例了，比如高宽比大于15的占比总量小于5%等。不过一些单元（如六面体）对大的高宽比不太敏感。

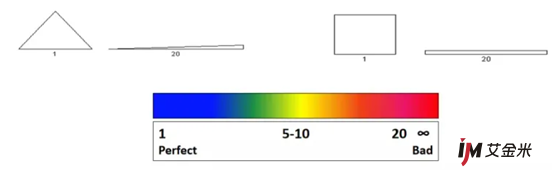
雅可比值。该比值基于雅可比矩阵的行列式，在有限元分析中，雅可比矩阵用于将单元矩阵从理论形状（如完全平方、三角形）转换为实际形状。理想单元的雅可比矩阵比为1，该值离1越远，该单元网格质量也越差。

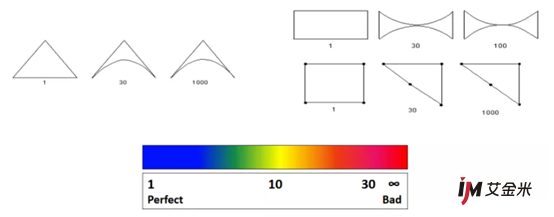
检查结果是评估网格的好方法，下面列出了几种方法：
查看未平均的结果。未平均的结果在节点处计算每个单元的应力值。每个单元在节点处计算的值会有所不同，从而导致节点周围的应力分布不均匀。有限元软件通常在节点处平均应力，以呈现光滑的应力云图，但这也不可避免隐藏应力的不连续性。粗网格比细网格有更高的应力差异，因此绘制非平均应力可以帮助用户识别网格细化的候选区域，还可以帮助你评估应力是否由于网格的原因导致被低估。

查看能量误差结果。能量误差显示节点上因应力不匹配而产生的能量。实际数字应该定性地处理，而不是定量地处理。这个结果是个相对值，色差明显的区域表明此处网格不够精确，如果发生在高应力区域，有必要通过加密网格来获得更准确的答案。

网格收敛性研究。从理论上讲，模型中使用的单元越多，计算结果越接近实际值。如果用户对网格进行细化并求解修正后的模型，经过多次迭代后，结果将趋向于稳定，这就是所谓的网格收敛。

有限元软件是一个非常强大的工具，它可以为设计提供深刻的见解，减少工程不确定性。然而，工具会受到输入的限制，如果输入不准确也就无从谈结果的准确性，其中网格是输入中的关键部分。划分网格之前，工程师们考虑自己分析的条件和关注的因素，有利于防止划分网格时眉毛胡子一把抓的现象，同时通过批判性地评估结果可以帮助我们更好地去提高结果的质量。

来源：三维机械设计工程师