直通管电声类比模型

最简单的模型
(为简化讨论,以下讨论均未考虑管内摩擦和辐射声阻Rm)
通常来说,可以认为声质量

其中p为空气密度,lx为管长,S为管截面积
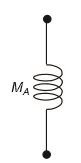
转换为阻抗型等效电路模型,见下图
不同模型适用范围
由于模型是建立在一定公式简化的基础上的,管长和声波长度之比对等效电路模型有效性会产生比较明显的影响。 不同前提下的模型误差也是不一样的。
具体可以参考下面的图表
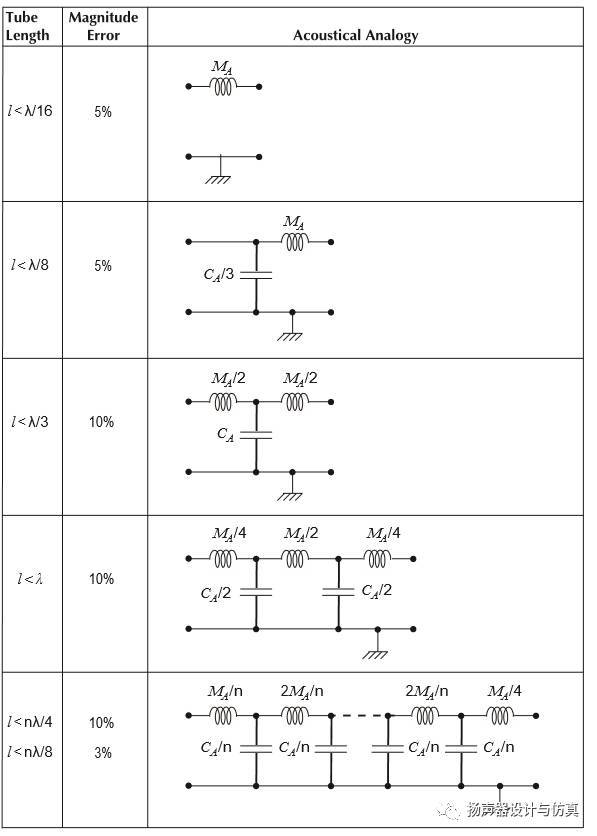
其中CA为等效声容

c为声速
末端修正
以上讨论均未考虑管出入开口对声负载的影响

仅讨论出口无限大障板的末端修正,接近倒相管的应用
其类比的附加质量(未考虑辐射声阻Rm)

其中a是管半径
包含末端修正的近似等效电路模型

以上末端修正模型成立的前提条件是管的直径远小于声波波长,否则需要另外探讨,比如采用声学有限元/声学边界元等工具进行分析。
而且该模型只适用于小信号的激励。如果风速过大,将导致湍流,从而会存在强烈非线性,使得模型失效。 任何一个模型都有其适用的范围。
登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2022-11-01
最近编辑:2年前
相关推荐
最新文章
热门文章