如何用matlab证明人耳对声音的相位不敏感?
作者利用matlab对声音的相位进行变换,来探索人耳对声音相位是否敏感。希望对各位有所启发。
以下是原文
=======================================================
提供一个思路:可以设计一个相频特性比较崎岖的全通滤波器,把语音滤波后再听,看看跟原来一不一样。
全通滤波器的相频特征能不能设计得比较崎岖,我已经记不得了,需要去复习数字信号处理了……
实验成功!
先来讲一下全通滤波器的原理。最简单的全通滤波器,只有一个极点和一个零点,极点和零点的辐角相同,模互为倒数。可以验证此滤波器在单位圆上的幅度响应为常数。
但这种一阶全通滤波器的极点和零点不构成共轭复数对,它的系数就也是复数。为了得到实系数滤波器,就要在极点和零点的共轭位置再增设一对极点和零点,如下图所示。
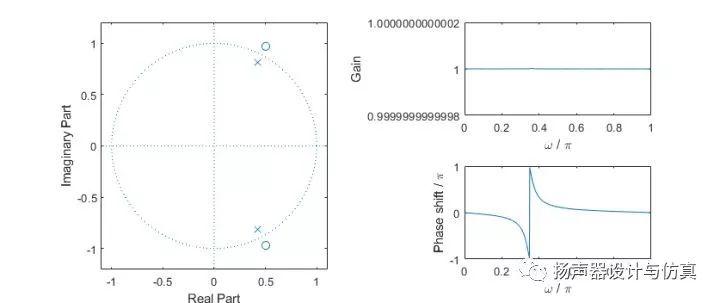
这种实系数二阶全通滤波器,幅度响应为常数,相位响应在 0 到 pi 角频率上会降低 2pi。极、零点越靠近单位圆,相位响应的变化就越偏离线性。
如果把多个这样的二阶全通滤波器级联起来,就可以得到一个幅度响应为常数、相位响应非常崎岖的全通滤波器。把一段语音通过这个滤波器再播放出来,就可以知道相位对听觉的影响了。

如图,我随机生成了 10 个靠近单位圆的零极点对,搭建了一个 20 阶全通滤波器。可以看到幅度响应的确为常数(那点波动是纯数值误差,可忽略),但相位响应十分崎岖。
右上角的图是清华电子系 2008 年夏季小学期 Matlab 课用过的男声「电灯比油灯进步多了」的波形,右下角是滤波后的结果。二者看起来区别就不大,播放滤波后的结果,听起来更是与原始声音毫无区别。于是可以证明人耳对相位不敏感。
实验用的代码如下,你也可以换用任何一段声音。
N = 10; % 零极点对数
pole_phi = rand(N,1) * pi; % 随机生成极点辐角(都在 z 平面上半部分)
pole_r = 0.9 + 0.09 * rand(N,1); % 随机生成极点的模,尽可能靠近单位圆
pole = pole_r .* exp(1i * pole_phi); % 算出极点的值
pole = [pole; conj(pole)]; % 让极点组成共轭对
zero = 1 ./ pole; % 算出零点的值
b = poly(zero); a = poly(pole); % 由零极点算出滤波器系数
b = b / sum(b); a = a / sum(a); % 归一化,让滤波器的增益为 1
[x, fs] = audioread('diandeng.wav'); % 读取声音波形,旧版本 Matlab 用
wavready = filter(b, a, x); % 对声音进行滤波
sound(y, fs); % 播放滤波后的声音
% 下面全是画图
% 1. 零极点图
subplot(2, 3, [1 4]);
zplane(zero, pole);
title('Zero-Pole Plot');
% 2. 幅频、相频响应图
n = 1024; m = n / 2 + 1;
% FFT 点数
H = fft(b, n) ./ fft(a, n); % 传输函数
H = H(1:m); % 由对称性,只保留一半
subplot 232
;plot(linspace(0, 1, m), abs(H)); % 画幅频响应
xlabel('\omega / \pi');
ylabel('Gain');
title('Amplitude Response');
subplot 235;
plot(linspace(0, 1, m), angle(H) / pi); % 画相频响应
xlabel('\omega / \pi');
ylabel('Phase shift / \pi');
title('Phase Response');
% 3. 声音波形图
t = (0:length(x) - 1) / fs; % 时间轴
subplot 233;plot(t, x); % 画滤波前的声音
xlabel('Time / s');
set(gca, 'YLim', [-1 1]);
title('Original Waveform');
subplot 236;plot(t, y); % 画滤波后的声音
xlabel('Time / s');
set(gca, 'YLim', [-1 1]);
title('Filtered Waveform');




