超薄防护性网布和防水透气膜的声学建模
[已获授权。公式太多,不好排版,将就着看。]
超薄防护性网布和防水透气膜的声学建模
杰森麦金托什[1] 瓦斯科马雷利[2]
(纱帝股份,阿皮亚诺真蒂莱,意大利)
[1]Email address:jmcintosh@saati.com
[2]Email address:vmarelli@saati.com
摘要:
当前,所有具备声学功能的消费类电子产品往往都在出音口的位置,使用精密编织的声学网布和防水透气膜来实现扬声器和麦克风的防护。此材料可以有效防止诸如灰尘、金属粉尘、水、油以及化妆品之类的外来污染物。从直径1毫米的麦克风模切件到直径8英寸的扬声器网罩,此材料均可保证声学性能的一致性。所以,其声学建模技术能识别重要的声学行为,包括这些材料传播声音时的振动模式,阻碍声音传播的“**振”,导致麦克风灵敏度损耗和扬声器共振频率上移的低频刚性等等。请注意材料透过性的“泄露”性能对限制以上所述的后两种效应的重要性。本文将呈现经改进的专有仿真建模工具不仅可以对材料及其可能的行为做出仿真,而且可与试验测量的阻抗结果准确关联。
关键词:声学建模,声学网布,薄板,防水膜
0 引言
几乎所有的具备音频功能的消费类电子产品都需要对麦克风和扬声器器件做某些保护。这种保护能使这些声学器件免遭大大小小的异物的损坏。大的异物可能是用户的手指、钢笔或者可能会与这些部件接触并以难以预料的方式破坏这些部件的其他异物。小的异物包括随着时间逐渐积累的粉尘和碎屑。可以是空气中漂浮的粉尘颗粒、风沙或者用于携带这些设备的口袋内的各种小颗粒。扬声器通常会使用强磁性钕铁硼磁铁,此磁铁具有极强吸附金属颗粒的能力,可能会引起潜在风险。在工业环境中,金属颗粒问题尤其麻烦,口袋和提包中常见的钥匙和金属盒能够产生小的含铁颗粒,并被强磁性的扬声器磁铁吸住。这些金属颗粒随时间不断在扬声器内积累,降低其中频段灵敏度。最终导致扬声器膜片负荷不均,进而导致异音问题,以至于扬声器最终被损坏。
此外,还需预防液体和糊状物。水几乎无处不在,但好在它最终会蒸发掉。而油、糊状物和粉状物也是一个大问题。当把手机放在面部接打电话时手机会与人分泌的油脂以及涂抹的各种化妆品接触。耳塞装置须对抗不同粘性和数量的耳垢或耳屎问题。厨房内还经常有食用油类和其他污染物。
随着移动电话、平板电脑以及其他声学设备充斥我们的生活,我们希望它们不仅仅能在干净有序的居住和工作场所中性能良好地工作,也能在各种环境中工作。在较为恶劣的环境下不仅不会损坏而且还要性能良好,这就对消费类电子产品提出了更高的要求。诚然,生产商已经大幅提升了这些设备的性能,今天制造的很多手机和平板电脑都是“防水”的,可浸没于水中或防止水溅入设备。在严格测试条件下,防水设备的性能尤其难以实现。
在这类环境下实现保护,需要采用超薄的保护材料,比如覆盖扬声器或麦克风的声学网布或防水膜。其中一个重要功能是避免异物侵入。鉴于大部分这类产品的尺寸均受到严重限制,应优先考虑较薄的材料。对于这类材料除了保护性能方面的要求外对其声学性能也有一定的要求。通常这些材料最好是“透声的”,也就是说放置在扬声器或麦克风前面时应具有较低的或不显著的灵敏度损耗。但是,由于这些材料对音频部件的积极作用,有时也会特意选择这类材料。对于扬声器尤其如此,扬声器中声阻尼会降低与共振有关的共振峰影响及谐波失真。
纱帝是意大利的一家跨国公司,专注于为声学市场提供材料的解决方案。SAATI的材料科学家和研发团队遍访世界各地的消费类电子产品设计师和制造商,熟悉他们在保护与声学方面的需求。通过定制产品解决方案和优化的专有声学仿真软件等工具提供技术支持。
声学材料的声学建模不仅可以让设计者仿真其效果,而且更为重要的是能够让设计者了解材料自身的性能。本论文将探讨这些材料的一些声学行为以及如何为其建模。
1 薄板和防水膜行为
为了保护扬声器或麦克风一类的声学器件,材料必须要覆盖声学器件与外界相连接的出音口。当声音通过出音口时,材料开始运动以便声扰动能够通过。声扰动通过后,声学材料必须要能够返回到其初始的零位移状态。根据材料是板状还是膜状或者兼而有之,使材料返回到零位移状态的力是不同的。
“薄板(板)”是具有内在刚性可以抵抗外力的一种较薄的材料。一旦外力(比如声压)从薄板上消除,由于来自材料内部的弯曲,应力薄板会回到其未弯曲时的状态。这些弯曲应力简称为“恢复力(restoring force)”。“防水膜(膜)”是通过拉伸覆盖在开口上的一种薄的材料。这种拉伸在材料上产生一个张力。当防水膜发生弯曲,这种张力可以提供一种恢复力使膜返回至其初始位置。
薄板的静态方程可以用四阶的Kirchhoff-Love薄板方程来描述[1]

其中,w是垂直于薄板平面方向的位移,P是作用于薄板两个曲面的压强,D是抗弯刚度,由下式计算

E是杨氏模量,h是板的厚度,n是泊松比。膜的静态控制方程是由泊松方程给出的二阶方程[1]

其中T是膜内的张力。注意压力P位于薄板方程1和膜方程3之间。当材料同时具有板和膜的特征时,压力P必须通过这两个弯曲力来平衡,或者

方程4表示的是作用于薄板上的静态力(即不随时间变化),同时包括板弯曲力(受D控制)和膜张力(受T控制)。该方程不包括薄板内材料质量作用(mass reaction)的动态效应(即随时间变化)。该质量作用实质是牛顿第二定律F=ma的“质量乘以加速度”部分。将该项加到方程4得到
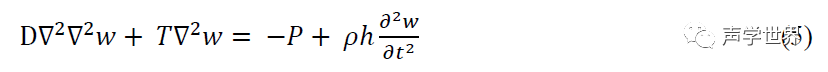
其中r是材料的密度,h是厚度。关于时间谐波条件,假定变量具有ejwt时间依赖性,方程5的二阶时间导数可以用-w2乘数替代,或者

这是我们的材料运动行为的最终表达式。方程6适用于同时具有薄板和膜行为的材料。如果D>0且T=0,材料将表现为纯板。如果D=0且T>0,则材料表现为纯膜。通常情况下是D>0且T>0,在这种情况下方程6为复合的板/膜解决方案。
2矩形板和防水膜的解决方案
方程6解决方案可以通过使用本论文中未讨论的数值技术和固支边界条件获得[8]。一旦位移w已知,声阻抗按以下计算

其中U为材料的体积速度位移(volume velocitydisplacement)。下标“PM”表示该阻抗来自材料的板/膜行为,对以后的区分很重要。当使用SI单位时,Z的单位是Pa/(m3/s),在本论文中也称作“声学欧姆”。U经由穿过材料表面的净体积位移(net volumetric displacement)计算

其中积分是遍及材料表面S积分。体积速度(volume velocity)U是V的时间导数,即U = dV/dt。在此假定具有ejwt时间依赖性,时间导数使用jw乘积因子代替,或者

举个例子,我们假定一个沿x轴长Lx沿y轴长Ly的矩形材料,使用以下数值参数

根据这些参数解方程6并使用方程7-9计算阻抗得到的阻抗曲线见图1。其中有一些重要特征需要指出。一是图1a的实部对所有频率值均为零,这是因为没有阻尼。通过构建E或T复数阻尼增加。一般通过在表达式中增加一个“损耗角正切(loss tangents)”实现,形式为

其中Eo和To是纯实数,qE和qT是以弧度表示的损耗角正切。当使用非零的损耗角正切时,阻尼将会施加于系统,实部为非零。另一个需要指出的特征是在低频时虚部遵循1/jw行为,表明这是类似弹簧的行为。因此,在非常低的频率时,材料表现出类似弹簧的行为,几乎没有质量惯性效应(mass inertia effects)。在5414 Hz,阻抗的虚部越过零,表明一种模式。另一次通过零点是在8850 Hz时。零阻抗说明在该频率下声音可以很容易的穿过材料,材料对于声音来说是“透明的”。 图2为材料在这些频率下的位移变形。5414和8850 Hz下的形状对应于图3中的(1,1)和(1,3)模式(这些模式的精彩动画演示见Dan Russell的文献[3])
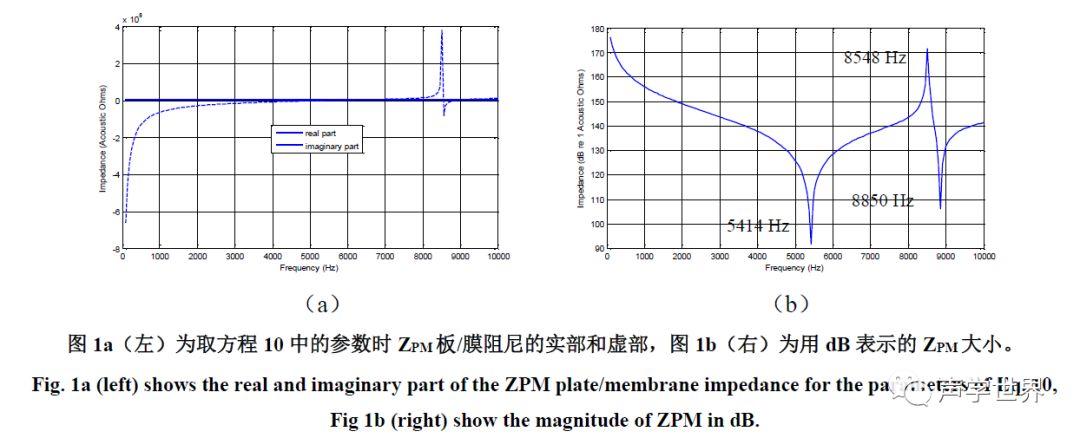
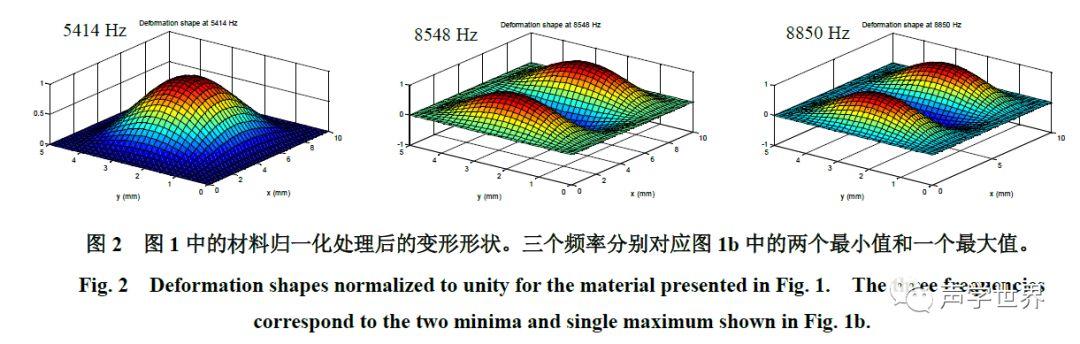

图1b中有两个最大值:一个在0Hz,或直流,另一个在8548Hz。第一个最大值是因为0 Hz, 或直流,对应的是“风(wind)”,风不可能通过由不透气材料做成的薄板,因此阻抗为无穷大。8548Hz时的最大值则有意义得多。在该频率下净体积位移为零,导致体积速度U为零,阻抗Z为无限,或当阻尼增加时至少是非常地大。Morris[2]将这种行为鉴定为“**振”并指出它们恰好出现在一共振下面,那里波节线有机会充分移动导致净体积位移等于零。把不透性的板或膜用于声学应用时,因为在这些频率下声音无法通过材料,“**振”就会成为很大的问题。代表着有限数量弯曲能量损失(bending energy loss)的非零损耗角正切可以防止该阻抗变得“无限大”,但是阻抗仍然相当高导致音频设备频谱上的“哑区(dead spots)”。由此可见解决这类“哑区”的一种方法就是将材料做成“泄露性(leaky)”的,可以限制最大阻抗。
最后,图3的模式按上升频率顺序出现,即(1,2)将比(1,1)在更高的频率出现,(1,3)将比(1,2)在更高的频率出现,以此类推。在我们的模拟中,5414 Hz共振是(1,1)模式,8850 Hz共振是(1,3)模式,但是(1,2)模式出现在它们之间但在阻抗曲线上看不出来。如果模拟扩大至更高频率也没有(1,4),(2,1)或(2,2)模式的迹象。这是因为沿材料的表面压强P是相同,不会引发无净空气位移(air displacement)的对称模式。即便会引发,因为这种模式下无净空气位移,也不会对线性的声学行为产生影响。 (注意这与“**振”的影响是不一样的,这不是一种真实的模式。关于板和膜的一篇更为精彩深入地陈述见Mellow的文献[7])
3 泄露性材料的效果
至此,我们仅讨论了表现出板和膜行为的材料。讨论中有个固有的概念就是这些理论上的材料都是不透性的,即空气无法流过它们。但是,几乎所有的声学材料比如声学网布都是属于可透过性。在这种情况下,声音还有通过材料的第二条路径:它可以穿透材料的孔隙(或通道)。具有这种孔隙的材料简称为是“泄露性的”,其中一个例子见图4。

在这两个路径的集总参数模拟中,它们表现为并联阻抗(图 4e)。板/膜行为的阻抗在第2部分中已论述并见图1。通过材料孔径的阻抗的确具有一些最低限度的频率依赖性[4];但是可以简单地处理为约等于Ro[5]。
此外,Ro可以通过流过材料的静态流动阻力(static flowresistance)估算。即稳定的气流穿过材料的“DC 直流”阻力。如果DP是流过材料的压力降,V是流过材料的颗粒速度,见图4c,那么

当DP单位取Pa,V单位取m/s,那么Ro单位为MKS Rayls。注意Ro本质上是表面积归一化了的,因此代表的是一体积(或固有的)材料属性。如果我们假定通过声学材料的颗粒速度沿材料表面S是相同的,那么乘以面积S后颗粒速度转换成体积速度,或U=V*S。那么流动阻力Ro表面积S的材料的声学欧姆值计算就是用Ro除以表面积S。材料的最终阻抗就是材料的板/膜阻抗ZPM和以声学欧姆表示的流动阻力的并联值,或

其中Zmat是“泄露性”材料的阻抗,即本论文的主要议题。两阻抗并联的一个重要性质就是并联后的阻抗值不能大于并联前两阻抗值中的任何一个,或

通过材料的Ro“泄露”是有极大意义的。假定图1模拟中使用的材料的Ro值取260 MKS Rayls,结果见图5。在这种情况下,低频和**振时的极端阻抗大大降低,在这些频率下实质上材料表现出纯阻性。因此,这是泄露性保护材料的主要优势。但是,在共振态时,阻抗仍然降至极低值,在这些频率下材料实质表现出无阻抗,即对声音来说是透明的。


4 材料的实验测量
本部分将不同种类的保护性材料的实测阻抗值与按照前述方程模拟的泄露性板/膜阻抗值进行了关联。
实验设置使用Ares声学仿真软件和测量系统采集由材料产生的声阻抗的实数和虚数。如在之前部分看到的,通常非透过性材料会以难以接受的方式减低消费性电子产品的声学性能,因此泄露性保护材料是一种常用选择。最佳地兼顾了声学性能和保护性能的泄露性材料主要有三类:声学网布,防水膜和复合材料(声学网布和防水膜的复合材料)。
声学网布是透过性最好的材料,因为有大的开孔(典型的7-400μm),“泄露”部分的贡献较大。由于其厚度(30-450μm)及几何构型它还拥有高的稳定性,因此如果暴露面积足够大的话“振动”对声音传播的贡献就会很有限。图6a为移动电话中实际使用的典型侧向扬声器的带有**面声学网布的声阻抗实数和虚数的测量值与模拟值的比较。

在一典型的侧出音扬声器配置中,建议使用优化的声学网布,其对声音传播来说尽可能是透明的,同时还能提供高水平的保护,避免外部污染物侵入。这种情况下,声阻抗主要来自阻性贡献(实数),如图6a所示几乎是一条平直的线。
图6b同样是Acoustex 080,但是样品尺寸较大(10.6mm x 5mm)并特意挑选以便能凸显出我们感兴趣的频率内的共振和**振。数学模型可以正确预测声阻抗实数和虚数的共振和**振。
第二类起保护作用的泄露性材料是防水膜。这些声学材料一般很薄,要比声学网布具有更高的流动阻力Ro,因此在预测其行为时板/膜振动贡献变得更加重要。典型地,起保护作用的泄露性膜厚度在几微米至50微米之间,与声学网布相比弹性模量更小(二者量级为10-200MPa与100MPa-300MPa)。泄露性防水膜平均孔隙尺寸小于1微米,因此使其更适用于小面积上的液体防护,比如微机电系统麦克风(MEMS)的保护。图7是面积为3的普通泄露性防水膜的例子。使用防水膜的已知参数,模型可以预测得到经实际测量得到的行为。注意随着频率向100Hz降低,声阻抗增加。在这些频率下防水膜的刚度开始支配其行为导致1/jw行为,但是大的流动阻力Ro制约着阻抗。大的(但有限的)Ro值是因为防水膜的孔径太小。同时,防水膜太轻了,第一种模式上移至超过7kHz,因此在该频率范围内无**振。

最后一类为复合材料,以SAATI H68T02为例,它是将一种很轻的防水膜材料粘接到一个声学网布上。它具有复合材料的特点:有类似声学网布的厚度和坚固性以及类似于防水膜的孔径尺寸。其可能的应用领域与防水膜类似,但是由于有网的支撑,结构更加稳定,比如可以承受较高的压力,可保护MEMS MIC免遭数米水柱压力的破坏。其声阻抗也是声学网布和防水膜的复合,见图8。结果是这种复合材料具有类似于声学网布的较平坦的频率响应,高频率下有小的类似于防水膜的共振;所有这些都被本论文中推荐的数学模型很好地预测到。

5 总结
超薄的声学材料通常应用于音频领域,其对声学器件(扬声器和麦克风)起到显著的保护作用,同时,又能提供良好的声学性能。本文给出的模型主要考虑了材料的三个重要物理特征:弯曲力(bending force),张力(tension forces)和允许直流空气的多孔材料透气性。以声学网布、防水膜和防水膜-声学网布复合材料为试验样品,使用该模型计算的声阻抗值与实测值匹配良好。关于该主题未来的工作将侧重于能够更好地估算材料性能,并将这些数据输入到ARES仿真软件(simulator)改善对这类材料的建模仿真。
参考文献
[1] TimoshenkoS, and Woinowsky-Krieger S, Theory of plates and shells, McGraw-Hill, 1959.
[2] Morris P, Vibration and Sound, McGraw-Hill,1950.
[3] Russell D,https://www.acs.psu.edu/drussell/Demos/rect-membrane/rect-mem.html.
[4] Attenborough K, Acoustical characteristicsof rigid fibrous absorbents and granular materials, Journalof the Acoustical Society of America, 73(3) March 1983: 785-799.
[5] McIntosh J, Lambert R, Nonlinear wavepropagation through rigid porous materials. I: Nonlinear parameterization andnumerical solutions, Journal of the Acoustical Society of America, Vol. 88,1990: 1939-1949.
[6] ARES Acoustical System is a product of SAATIS.p.A., saati.com, support.ares@saati.com.
[7] Mellow T, Beranek L, Acoustics: SoundFields, Transducers and Vibration, Second Edition, Ch 14, Academic Press, 2019.
[8] Burden R, Faires D,Numerical Analysis, 3rd Edition, Prindle, Weber & Schmidt, 1985.
[9] Acoustex™ is a line of acoustic woven meshproducts from SAATI, S.p.A., saati.com.
通讯作者
杰森 麦金托什 博士,于1992年获得明尼苏达大学博士学位,专业为多孔材料非线性行为。他的工作主要是HVAC和耳机有源噪声控制,通讯设备声学建模,医疗设备实时超声跟踪。他是Ares声学仿真软件和测量系统的主要设计者。
瓦斯科 马雷利,于2016年获得意大利英苏布里亚大学科莫分校理学硕士学位。2017年起任SAATI S.p.A声学研发团队初级科学家,目前居住在意大利科莫。主要工作是声学材料理论行为研究,测量其主要特性并与模拟结果进行比较。他利用自己的知识针对客户的具体用途帮助客户选择最适合的材料。
译者
赵雷,中国人民大学硕士研究生,Audio Engineering Society音频工程协会会士,就职纱帝技术网布(天津)有限公司任声学部门中国区业务发展经理,从事声学网布非线性和防水透气膜应用的相关研究。