【往年优秀论文赏析】感应加热数值仿真及其并行加速性能测试
摘 要:以内嵌金属颗粒的石墨球为研究对象,基于感应加热基本理论,建立了电磁场与温度场耦合的有限元数学模型,利用通用多物理场分析软件ANSYS 对金属石墨球的感应加热过程进行了数值仿真,计算中考虑材料随温度变化的非线性特征,采用多场顺序耦合方法,得到了石墨球温度随加热时间变化规律,并对不同频率和电流密度下石墨球感应加热效果进行了对比分析,计算结果为石墨球感应加热实验的开展提供参考。同时,基于上海超算中心“蜂鸟”高性能计算平台,探讨在不同核心数下求解多场问题的并行效率,为该类问题的大规模并行计算以及更好发挥并行计算优势提供参考。 感应加热是利用电磁感应在导体内产生涡流热效应来加热工件的电加热,该方法以其效率高,控制精确,污染少,安全性好等优点在工业生产中得到广泛应用。感应加热过程是电磁感应和热传导过程相互作用的综合体现,电磁感应过程中所产生的涡流功率为热传导提供所需的能量;热传导过程导致的工件温度分布反过来会影响工件电磁感应所产生的涡流大小。通过现有理论很难求得感应加热下工件的温度场分布,而基于传统的实验设计方法耗时费力,成本 高昂,如果物理模型复杂且实验危险,无疑增加了这类问题的难度,目前针对感应加热器的设计以及工件的涡流效应分析大多是根据经验公式和实验进行测算。
计算机数值模拟方法已经成为求解感应加热等复杂场问题的有效工具,1996年,K.Sadeghipour等人利用ANSYS软件有效地进行了钢板电磁场和温度场分析,数值模拟的结果得到了试验的验证;陈慧琴等用有限元分析方法研究了机车曲轴坯弯曲镦锻前的感应加热过程, 得到了坯料内的温度分布以及温度随时间的变化规律,并与现场实测值进行了对比;帅克刚等人在船外板结构的热弯曲成型工艺中建立了感应加热热源有限元模型,分析了高频感应加热温度场变化,并通过实验结果验证了模型的有效性。基于数值仿真方法研究多场问题在众多行业中得到应用,但很多的应用中或没有考虑多物理场的耦合关系,或没有考虑材料非线性特征,研究对象相对简单,实际上采用数值仿真的方法可以求解更为复杂的多物理场问题。
本文以内镶金属颗粒的石墨球为研究对象,建立了电磁场与温度场耦合的有限元数学模型,基于多场顺序耦合的方法,利用通用多场分析软件ANSYS对石墨球的感应加热过程进行了数值仿真,考虑材料非线性特征,得到了石墨球温度随加热时间变化规律,并对不同加热频率和电流密度下石墨球感应加热效果进行了分析,本文全部计算借助上海超算中心“蜂鸟”集群完成,最后还就如何有效利用高性能计算资源解决多场问题进行了探讨。
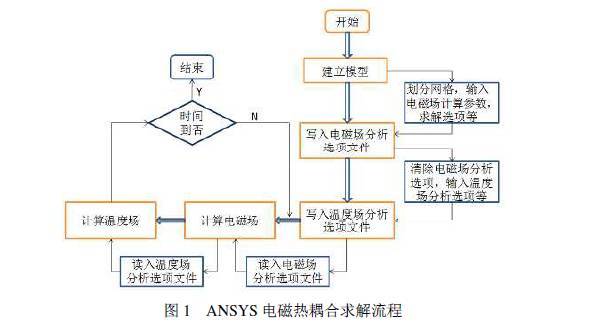
感应加热是由工件上的感应电流产生涡损而引发的,工件温度的升高反过来又引起工件材料导电、导磁性能的变化,在ANSYS软件上模拟感应加热的关键是研究多场耦合问题。多场耦合分析的方法有两种,一种是按顺序进行电磁场与温度场的分析,它通过把电磁场分析的结果作为瞬态热分析的载荷实现多场的数据传递,每一次迭代修改材料的属性重新计算,即顺序耦合法(Sequential Coupling Method);另一种方法是把电磁场与温度场控制方程耦合到一个方程 矩阵中求解,即直接耦合法(Direct Coupling Method),这种方法很难把多场求解技术真正结合到一起。对于感应加热不存在高度非线性相互作用的情形,采用顺序耦合法更为有效和方便。顺序耦合法每隔一定的时间间隔要重新进行电磁场的分析,以便对那些受温度影响较大的材料物理参数进行修正,然后再给加热工件施加新的热载荷,从而完成不同物理场之间数据的交换,直到收敛到一定精度为止,顺序求解电磁热耦合计算的流程如图1所示。
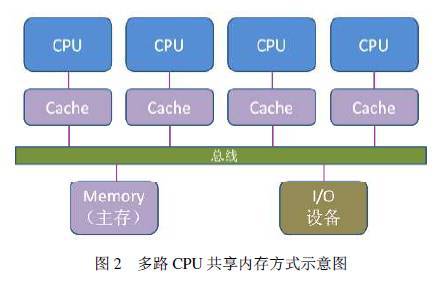
ANSYS软件支持“share memory”和“distributed memory”两种并行方式。“share memory”是共享内存式并行计算,指单机多CPU的并行;“distributed memory”是分布内存式并行计算,指多机多CPU的并行,一般来说,分布式并行往往比共享内存并行有更好的并行效率,但并不是所有类型的计算都支持分布式计算,对于多场顺序耦合问题,ANSYS软件只能采用共享内存并行方式。图2显示了在一个计算节点内使用总线将CPU与主存I/O处理设备相连示意图,各CPU 通过共享同一内存地址空间相互通信,由于总线带宽限制,共享内存的CPU个数往往有限,本文中只需要通过ANSYS命令行-NP选项即指定共享内存并行处理器的个数。 感应加热实质是在交变电流作用下在导体内部产生涡流热来加热工件的一种电加热方式,主要包含了两种物理过程,一种是生热过程,即将电能转换成工件内的热能,其基本原理可归结为电磁感应定律和焦耳楞次定律,一种是传热过程,包含了工件的热传导以及工件与外界的热交换。根据麦克斯韦微分方程,通过引入矢量磁势Ar和标量电势f ,推导可知在感应加热时工件导体内的涡流由下面控制方程确定:

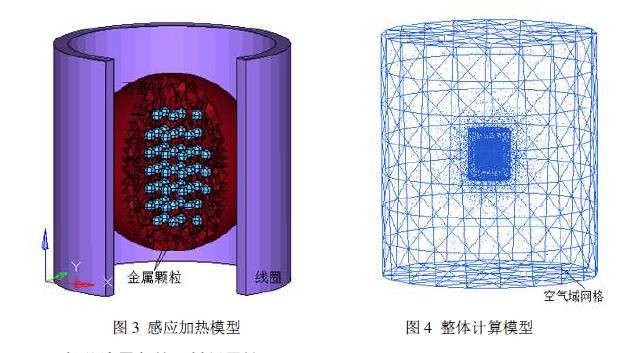
对内嵌金属颗粒的石墨球感应加热来自一个实验构想,通过数值仿真方法和相似关系对实验可行性和实验效果进行预判。真实的金属石墨球实验装置结构非常复杂,一开始精细化建模大规模求解也不科学,因此有必要对数值模型进行合理的简化。简化后的石墨球感应加热模型如图4 所示,感应线圈内径,外径,高分别为40mm,35mm,40mm,直径为30mm 石墨球位于感应线圈正中,内部均匀的分布直径为2mm 的铁质金属颗粒251 个,整个感应装置包裹在一个直径为400mm,高度为450mm 的圆柱体空气单元中。计算中,电磁场分析采用solid97 单元,温度场分析采用solid70 单元,不考虑材料应力应变,在划分网格时,不同材质之间采用共节点方式连接,在集肤效应深度内处适当加密网格,整个计算模型四面体和六面体的单元总数超过20 万,整体计算模型网格如图4 所示。
石墨球感应加热边界条件较为复杂,为了缩短石墨球预加热计算时间,初始温度设定为450℃,感应加热过程中,当石墨球外表面温度达到750℃时,保持该边界温度恒定,以此来模拟石墨球外部环境温度和换热边界,暂不考虑边界上辐射换热,设定石墨球加热时间为20s。对于电磁场分析,空气外表面近似满足磁力线平行边界条件,其他部位满足磁力线垂直边界条件。已知金属颗粒的相对磁导率(MURX),电阻率(RSVX),热导率(KXX),焓变(ENTH), 采用随温度变化的函数,石墨球相对磁导率为1,电阻率为1.56E-05W×m ,石墨热导率,焓变值采用随温度变化函数,线圈和空气相对磁导率为1。 本节讨论的内容是基于感应频率为9KHz,电流密度为2.0e8A/m2工况下计算的结果。图5显示了石墨球中截面温度变化,在XOY 平面上可以看出,温度呈现中间高边缘低的环状分布特点;在YOZ 平面,温度也是呈现中间高边缘低的分布特点,远线圈端温度相对近线圈端温度低,石墨球内部高温区域呈现倒8 字形状。为了描述石墨球内部温度变化情况,在图5 所示XOY 平面上选取了若干位置点,这些关键位置的温度变化如图6 所示。在加热前8s,石墨球内部温度呈现快速上升趋势,越靠近石墨球外部,温度上升越快,由于在石墨球表面设置了热交换边界条件,使得感应产生的热量通过边界热交换带走,最终使得热交换和感应生热达到动态平衡,各观测点温度不在发生变化,石墨球内部最高温度在1040℃左右;石墨球外表面在感应加热初期,温度快速上升,当温度达到750℃后,保持该边界温度恒定模拟换热边界,E 点位置温度变化验证了这一点。
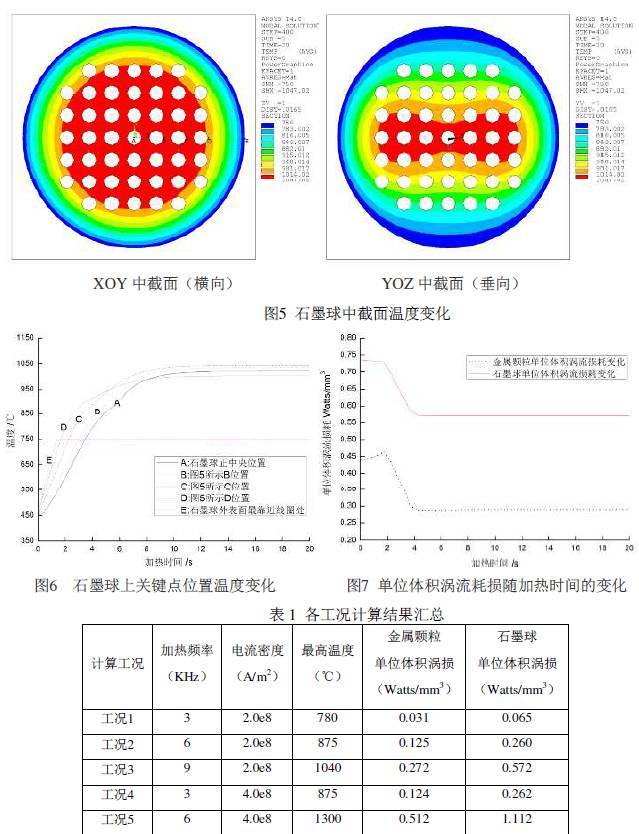
图7显示了金属颗粒和石墨球单位体积涡流损耗变化趋势基本一致,加热初始阶段,随着温度的上升,金属颗粒和石墨球涡流损耗约有起伏,随着温度的继续上升,与边界的热交换也随之开始,随着材料导磁率的下降,感应件涡流损耗呈现直线下降趋势,当内部温度趋于稳定后,金属颗粒和石墨球涡耗也不在发生变化,石墨球单位体积涡损约为金属颗粒单位体积涡损的2倍。表1对不同加热频率和电流密度下的计算结果进行了汇总,随着加热频率和电流密度升高, 石墨球能达到的最高温度依次上升,金属颗粒和石墨球单位体积涡损也呈上升趋势,从表中可以看出,加热频率和电流密度与感应件单位体积内涡损存在一定比例关系,当加热频率或电流密度变化一定倍数时,感应件单位体积内涡损变化该倍数的平方倍。
5.2 高性能计算平台并行求解
嵌有金属颗粒的石墨球感应加热数值模型涉及到多场耦合迭代计算,计算规模大,工况复杂,若用普通工作站单核求解,计算一个工况需要3-5天时间,倘若工况多,则对计算时间和计算效率要求更高,因此迫切需要借助高性能计算资源提高计算效率。上海超算中心为了增强向工业企业提供CAE/CFD仿真计算服务的能力,于2012年6月部署了一台运算速度为21万亿次/秒的IBM集群计算机,通过用户集体投票命名为“蜂鸟”集群,该集群包括65台HS23刀片计算节 点(Intel E5-2670,2CPU/16cores,2.6GHz,64G内存,L3缓存20M)。本文的计算全部在“蜂鸟”集群上完成。为了保证测试和对比结果更有说服力,测试前保证节点上无其他消耗计算资源的进程,算例在不同CPU 环境下相同设置求解2次,若2次求解的墙上时间差大于5%,则进行第三次求解,取墙上时间相近的2次数值取平均后作为最终统计结果。针对石墨球感应加热单工况,由于每个迭代步中求解的方程和自由度数相同,在进行多核并行计算测试中设置加热时 间为1s。
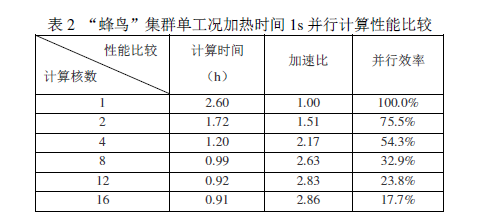
不同计算核心数下计算时间和并行加速性能如表2所示。随着并行核心数增加,计算时间都有不同程度的下降,当并行核心超过4个时,计算时间基本能控制在1小时内完成,随核心数增加,并行加速效果并不明显,并行效率呈现大幅下降趋势,究其原因,主要有如下几点认识:
1)使用单核计算时,高速缓存吞吐量有限,单核求解效率也不高,运行时间因而变长,随着核心数增加,多个数据缓存减少了单个处理器上内存总线和内存上的负载,使得它们可以被多个处理器共享,然而由于内存总线的带宽限制,使得加速效率呈现大幅下降趋势;
2)计算模型涉及到多物理场迭代,在形成方程组、结果后处理,多场数据交换等过程实际上是单核运行,真正的多核并行只发生在求解方程组时期,求解方程组时间占总计算时间的比重直接决定了多核并行计算效率的大小;
3)本模型通过读写数组方式对模型施加温度边界条件或存储温度结果,每
一次迭代过程都要对边界上温度进行判断,这些过程都是在单核下进行的,再多的核心也起不到加速效果,从而降低了整体多核并行效率。 本文以嵌有金属颗粒的石墨球感应加热过程为研究对象,基于电磁感应加热原理和有限元分析方法,研究了不同加热频率和电流密度下金属石墨球的加热规律,并基于上海超算中心“蜂鸟”集群,对求解这类问题进行了并行加速测试。结合前面的描述,主要有如下几点认识: (1)石墨球感应加热产生的热量最终与换热边界达到热平衡,各位置的温度不在发生变化,石墨球从内向外温度呈现递减趋势。随着加热频率和电流密度的增加,感应件最高温度随之上升,加热至最高温度所用时间也随之缩短。感应件涡损与电流密度和加热频率正相关,当加热频率或电流密度变化一定倍数时,感应件单位体积内涡损变化约为该倍数的平方倍。由于仿真模型和实际感应过程存在一定的差异,本文的所得出的结论仅为感应加热实验提供参考。 (2)对于多物理场顺序耦合计算,目前只能用共享内存并行方式,由于受算法并行度,总线带宽以及负载均衡等因素影响,使得这种并行方式加速效率并不高,随着软件版本升级和并行算法的完善,不排除以后会有更好的并行方式求解这类问题。针对这类问题,并行求解可以不同程度的降低求解时间,在提交这类任务时,应根据作业具体情况和硬件环境选择合适的并行规模,以此提高求解效率。 PS:由于**栏字数限制,本文只署名了第一作者姓名