案例分享 | 连接器结构几何参数优化

连接器结构被广泛用于各种工业领域，如电动交通、电力自动化或汽车行业。连接器设计的几何结构，需要实现功能所需的插入和拔出要求，同时必须保证连接器的质量。借助Ansys optiSLang，工程师能够有效地应对这些挑战，本文将介绍如何为连接器设置并开展自动参数标定与优化，以及后续的容差分析。

图1：敏感度分析得出的力-位移曲线（灰色）与拉伸测试参考曲线（绿色）比较

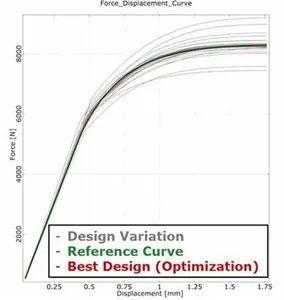
图2：最优力-位移曲线（红色）与拉伸测试参考曲线（绿色）比较以及从优化中得到的其他曲线（灰）

首先，连接器优化通常会涉及材料参数标定，例如在拉伸测试中进行非线性材料参数标定。材料标定的目的是找到用于描述材料法则的参数集，从而得出尽可能最佳拟合的参考拉伸测试曲线。弹簧钢的拉伸测试中已经开展了材料标定，并在optiSLang 安装步骤教程“spring_steel”中进行了具体介绍。本文只对材料标定的结果做简要介绍，对描述完整弹塑性材料行为的五个材料参数进行了标定。图1 所示的是拉伸测试获得的力 - 位移曲线（绿色）和敏感度分析得出的仿真曲线（灰色）。材料标定的结果如图2 所示。最优曲线（红）与参考曲线（绿）几乎一致，显示出极佳的拟合度。标定后的材料将用于后续仿真。本文介绍的连接器优化旨在实现所需的插入和拔出行为。

图3：仅包含载流组件的连接器的简化参数模型

为了进行优化，在Design Modeler 中生成了具有15 个几何参数的完全参数化 2D CAD 模型。图3 所示的是连接器设计，该设计只考虑了不带塑料组件的载流部件。然后基于CAD 模型，使用自动网格剖分功能在Ansys Workbench 中建立了有限元模型。组件1 被定义为固定在左侧。载荷工况包含两个有轴向位移的载荷步骤。组件2 在沿负x 方向进行轴向移动时代表连接，沿相反方向进行轴向移动时代表分离。插入过程和拔出过程会产生力-时间或力-迭代步曲线，如图4 所示。

插入过程从迭代开始到迭代步50 结束，拔出过程从迭代步50 开始到迭代步100 结束。连接过程由刚开始的负力曲线描述，然后用正力曲线描述夹口回弹过程。拔出过程由曲线后半部分开始处的正力曲线描述，然后用负力曲线描述夹口回弹过程。

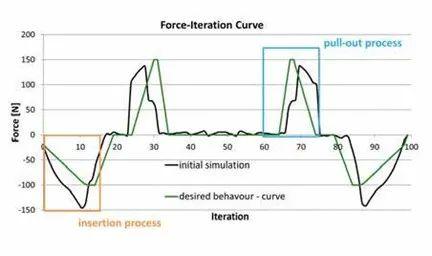
图4：设计参考力变化曲线（绿色）和连接器初始设计（黑色）的力变化曲线，并标示了关注的插入和拔出过程对应范围

参数标定的目的是最大限度缩小参考曲线与仿真曲线之间的偏差。参考曲线（图4 中的绿色曲线）由设计的预期功能相对应，并非如材料标定所做的那样从测试中获得。最小化也只能在标注区域中（图4 中的橘色和蓝色矩形）进行，这意味着不考虑夹口回弹行为。与锁紧力相比，初始设计（图4 中的黑色曲线）的插入力过高。根据连接器的功能需要，结构设计希望插入过程的力增长梯度尽可能的缓慢， 然而拔出过程的梯度应该更陡。在比较参考曲线和初始设计时，主要关注以下几点：

• 在插入过程中且较低的梯度

• 降低插入力（保持力的2/3）

• 在拔出过程中恒定且较高的梯度

• 较高的锁紧力（150N）

开展敏感度分析，以确定结果变量与输入参数之间的影响相关性。在本例中，使用的工具软件产品为Ansys optiSLang 7.1.0. 在预定范围内改变设计实验（100 种设计，ALHS）中的15 个几何参数。对于每一个几何结构变量，都会保存得到的力迭代曲线和创建的几何结构图像。在这100 种设计里没有出现“ 失败的设计”。

图5：在Ansys optiSLang中定义优化目标

敏感度分析结果是生成的信号和向量，即没有标量值。信号是定义的参考信号（预期值）和仿真信号，两种信号都可用于可视化和提取向量。对于插入和拔出过程对应的时间步（图4 中的标记区域），参考数据和计算数据间的偏差平方和也被定义为结果变量，其定义可参见图5，这个变量可在后续的优化中用作定义目标函数。偏差的提取来自于恒定参考信号和可变仿真信号的纵坐标值之差。

使用向量的优势在于可以最大限度地减小偏差，并为每个向量分量设置单独的MoP。此外，使用向量还可进一步检测到哪些输入参数何时在什么方向上产生影响。对插入过程和拔出过程分别计算对应迭代步的向量分量偏差，然后合并在一起。向量的离散化和长度是相同的，因此也不在插入和拔出过程之间进行加权。未定义其他边界条件（约束），在敏感度分析中已经设置了优化目标，因此能立即对结果进行分析。

图6：敏感度分析得到的力-位移变化曲线（灰色）与参考曲线（绿色）对比，以及敏感度分析得出的CoP矩阵

就参数标定而言，敏感度分析的一个重要目标是确保仿真模型的变化完全覆盖重要横坐标区域中的参考曲线。这样可以保证优化过程中在选定参数集的限制范围内实现最佳拟合。图6 中所标记的是两个受关注区域内的拟合情况。参考曲线（ 图6中的绿色曲线）在标记区域内被仿真曲线（图6中的灰色曲线）覆盖。

插入过程和分离过程的位移横坐标区域被划分成18 个等效步骤，并得到18 个向量分量。这可以用来确定哪些输入参数对信号特征有影响。两个CoP 矩阵中的每个向量的二阶分量如图6 所示。插入和拔出过程中的信号影响变化是可以识别的。排除了一些重要性可忽略的变量后，两个载荷工况的CoP 矩阵中，仅显示了插入过程的8 个输入变量和拔出过程的6 个输入变量。因此，敏感度分析中对15 个可变的几何参数进行参数降阶，可以得出最重要的和其次重要的若干个输入参数。所有未在此显示的输入参数，对于结果信号响应均不重要，所以会被自动过滤掉了。

在不对所有的参数进行单个敏感度详细检查的情况下，插入过程得出的总CoP 值高于92%。这表明，通过目前确定的关联性模型可以有力地描述了基本的物理现象。拔出过程的总CoP 值在56-76% 之间，没有表现出非常高的预后质量。这是由于几何结构变化较大而导致的不利设计，从而造成拔出力逐步增大。

在得到了标定后输入参数的重要性和敏感度后，就可以开展进一步优化以改进系统或产品设计。由于在敏感度分析中已经定义和分析了优化目标，因此可以立即以敏感度分析结果为起始设计进行优化。此外，敏感度分析还有助于简化设计，即减少输入参数和减小输入参数变化范围。总而言之，敏感度分析能够为即将开展的优化减少计算时间，并以更快的速度找到最优设计。由于拔出过程的预后系数CoP 较低，因此不能继续在MoP 上进行优化。为了进行优化，选择采用自适应响应面方法（ARSM）进行直接优化。

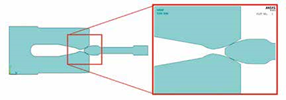
图7：参数标定得出的连接器几何结构最优设计

在敏感度分析过程中，未对响应变量产生任何影响的输入参数将不会参与优化。但是，在优化中考虑了它们的参考值。在图6 中，用最优设计曲线（红色）开展的优化显示与预期曲线高度一致。对于插入过程，在最大插入力下存在良好的拟合。遗憾的是，所需的插入力变化曲线拟合不佳。这是由于建模的接触区域的圆形表面，难以实现插入力的线性增长。相反，拔出过程的拟合度极佳。最大保持力和力变化都被较好的标定。图7 所示的是连接器的最优设计。

在连接器优化中，插入力和拔出力的绝对值是关键设计指标。例如当存在**的载流部件时，过低的拔出力可能会威胁生命。因此，在优化后应控制实际存在的几何加工参数偏差对拔出力的影响。

因此，需要通过容差分析来研究输入参数偏差将会如何影响力变化曲线、最大插入力100N 和最大拔出力150N，容差可能出现在材料、载荷或几何结构方面。在本案例中，研究15个几何参数的容差对插入、拔出力峰值和力变化曲线的影响。首先对15 个几何参数定义了相等的2% 变异系数（CoV）和正态分布特征。几何参数的基准值是之前直接优化得到的最优设计值。结果变量仍然是导出的力-迭代曲线，根据信号间隔提取的向量，以及最大插入力与拔出力。使用已在Ansys Workbench中使用过的相同全参数化2-D CAD模型进行仿真。15项几何参数已在设计实验（100种设计，ALHS）中定义。与敏感度分析相似，应明确结果变量与输入参数之间的影响关系。

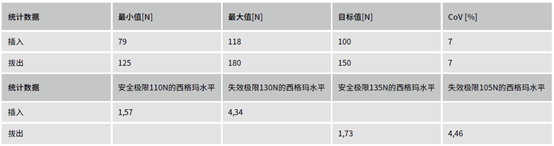
表1：容差分析得出的最大插入力、最大拔出力的正态分布统计值列表

表1列出了最大插入力和最大拔出力的正态分布统计值。最小值和最大值表明两个力在基准值（目标值）周围有很大的分散。此时，应考虑在Ansys optiSLang 中确定自主选择的安全极限和失效极限。在这里，这些极限值依惯例选定。每个极限都规定了西格玛水平。本案例中没有符合西格玛水平的规格。

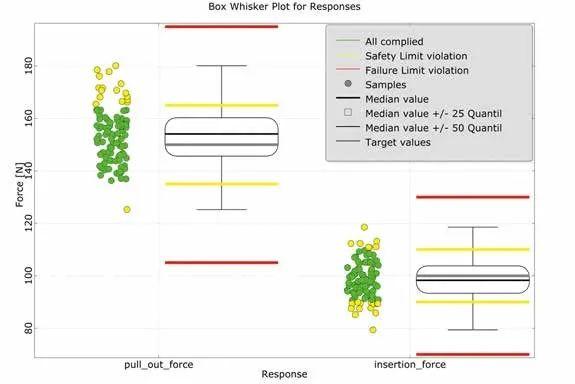
图8：两个结果变量的盒形图，将设计空间根据安全极限（黄线）和失效极限（红线）进行分区

另一项可视化结果是最大插入力和最大拔出力的盒形图（图8 ）。可以清楚地看到最大插入力、拔出力的非对称分布函数。可以计算并显示超过安全极限的概率。

在容差分析可以借助变异系数CoV 进行设计评估。如果结果变化范围的CoV 值小于输入变量的CoV 值，则该设计可被视为鲁棒性设计。查看表1 中两个结果变量的CoV 均为7%，而定义的所有输入变量的CoV 均为2%，表明该设计不具备鲁棒性。这里找到的最优设计参数值是不稳定的。即便是很小的输入参数离散分布范围，也将会导致较大的输出离散变化。

图9：容差分析得出的插入和拔出过程中CoP矩阵

为了确定影响最大的输入散射，必须分析CoP 矩阵。图9展示了插入过程和拔出过程以及最大力的CoP 矩阵。图9 中的两个CoP 矩阵仅显示了每个二阶向量分量。两种载荷工况的CoP 矩阵显示，只有插入过程的5 个输入散射和拔出过程的6 个输入散射具有不可忽略的重要性。

因此，可以对15 个离散分布的输入参数进行降阶，仅保留最重要和次重要的输入参数进行容差分析。对于插入过程以及最大拔出力，获得的总CoP 值较高，但小于96%。拔出过程的总CoP值在33-96%之间。同样，这也是不合适的几何结构参数定义造成的后果，导致拔出力阶跃增长。

显然，在容差分析中，与之前的敏感度分析相比，得出的重要输入参数是完全不同的。这是因为敏感度分析考虑的是全局范围，而容差分析中，它只是确定的最优值周围的局部范围。

通过几何参数标定的方式可以实现对于连接器几何结构的设计优化。敏感度分析帮助得出每个输入参数在插入过程和拔出过程对结果变量的影响程度。当CoP 值较低时，可以选取直接优化的方式进行标定。通过最大限度减小结果向量间的偏差，可以获得预期设计和仿真结果之间的高度准确的一致性。然而，随后对最大插入力和最大拔出力的容差分析中发现，最优设计参数值不具备鲁棒性。尽管如此，CoP 矩阵中的信息可以帮助设计者了解到必须减少那些输入参数的偏差范围才能获得稳健的设计，即提供给设计者公差设计方面的指导。