《流体力学通论》介绍——刘沛清

如果说现代文明起源于机械工业的兴起和发展的话，那么流体力学与机械工业的结合起到了决定性的作用，也可以说流体力学是机械工业现代化皇冠上的一颗耀眼的璀璨明珠。从古代的水力机械到现代最复杂的航空发动机的诞生均与流体力学的发展密不可分，也可以说流体力学几乎涉足到诸如水轮机、汽轮机、燃气轮机、膨胀机、风力机、水泵、风扇、通风机、压缩机、液力耦合器、液力变矩器、风动工具、气动马达、液压马达以及各种流体输运和控制设备等，所有以流体为工质来转换能量的机械。因此，毫无疑问，流体力学是机械工业最为活跃的一门专业基础学科，也是工科大学开设的一门专业基础课程。为了激发初学者的学习兴趣，便于了解流体力学基本知识和发展规律，本书是一本以传记形式和科普特色编著的流体力学通论。作者参照世界著名流体力学大师普朗特著《流体力学概论》、英国著名流体力学家巴切勒著《流体动力学引论》和《中国儿童百科全书》的编著理念，结合自己多年教学体会和经验，尝试一种将自然科学与人文历史相结合、知识传承与认知规律相结合的编纂模式，将抽象深奥的流体力学知识点打碎，从直观易懂的物理概念入手，以由浅入深、由表及里的方式，将流体力学发展史和基本知识有机结合起来，分八章将流体力学基础、空气动力学、水动力学、 计算流体力学、实验流体力学、风洞和水洞设备、飞行奥妙与空气动力学原理和流体力学人物志等八章介绍给读者，以便为初学者激发兴趣点、全面了解流体力学的发展和进一步深入学习提供参考。

本书适应于热爱流体力学的所有人们，包括大专院校的教师、研究生、本科生，从事与流体力学有关的各行业的技术人员和科学爱好者，部分内容也适应于初高中的广大学生。

以下摘自刘沛清著《流体力学通论》第一章的部分内容。

粘性流体运动微分方程与涡量输运方程

鉴于理想流体有势运动圆柱绕流无阻力与实际不符，人们开始研究粘性流体运动，基于牛顿內摩擦定律(1686年），建立了粘性应力与流体微团变形速率之间的本构关系，并在1755年欧拉理想流体运动方程的基础上，经过1822年法国工程师纳维（Claude-Louis Navier，1785〜1836年，如图1所示）、1829年法国科学家泊松(Simeon-Denis Poisson 1781～1840年，如图2所示)、1843年法国流体力学家圣维南（Adhémar Jean Claude Barré de Saint-Venant ，1797～1886年，如图3所示），最后由1845年英国科学家斯托克斯(George Gabriel Stokes，1819～1903年，如图4所示)在剑桥大学三一学院提出应力变形率的三大关系，完成了牛顿流体粘性运动微分方程，即著名的纳维-斯托克斯（Navier-Stokes）方程组，简称N-S方程组。即

其中，u,v,w分别为质点的速度分量；f_x, f_y, f_z分别为作用于质点上的单位质量力；p为作用于质点上的压强；ν为流体运动粘性系数；△为拉普拉斯算子。写成矢量形式为

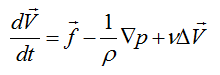
这个方程组说明，导致流体微团加速度变化的是作用于流体微团上的质量力、压强差力（表面法向力）和粘性力（表面切向力，反映在运动方程中表现为动量的粘性扩散行为。请注意这里无粘性耗散，粘性耗散只能出现在能量方程中）。

图1  法国力学家纳维（Claude-Louis Navier，1785〜1836年）

图2  法国科学家泊松(Simeon-Denis Poisson 1781～1840年)

图3   法国力学家圣维南

（Adhémar Jean Claude Barré de Saint-Venant 1797～1886年）

图4  英国力学家与数学家斯托克斯

(George Gabriel Stokes，1819～1903年)

玻尔兹曼方程与N-S方程比较发现，它们之间存在一定的关系，实际上N-S方程组是玻尔兹曼方程的流体力学极限。至此，从1755年导出理想流体运动的欧拉方程组到1845年导出粘性流体运动的N-S方程组，通过历时90年时间，数学家们为流体力学主要方程的建立与推导做出了卓越贡献。此后，流体力学开始进入到大量流动问题的求解过程和应用的阶段。

对于质量力只有重力、不可压缩粘性流体的定常流动，沿着流线积分N-S方程组，可得到类似于理想流体的伯努利方程，但在能量方程多了一项因克服粘性摩擦力做功而损失的机械能项。即

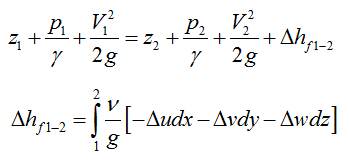
与理想流体伯努利方程相比，上式右边多出的项表示单位重量流体质点克服粘性应力做功所消耗的机械能，这一项不可能再被流体质点机械运动所利用，故称其为单位重量流体质点的机械能损失，这个损失与积分路径（流线的形状）有关。表明：在粘性流体中，沿同一条流线上单位时间单位重量流体质点所具有的机械能沿着流动方向总是减小的（如图5所示），不可能保持守恒（理想流体时，总机械能是保持守恒的，无机械能损失），流体总是从机械能大的地方流向机械能小的地方。

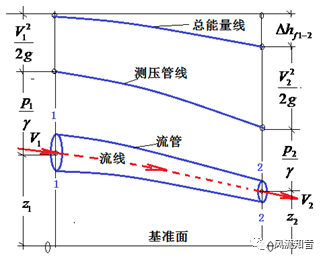
图5  粘性流体运动的能量方程

对不可压缩粘性流体运动的N-S方程取旋度，在质量力有势的条件下，可得到大家熟悉的涡量输运微分方程（类似于理想不可压缩流体的亥姆霍茲涡量方程），即

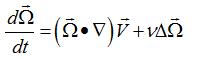
式中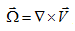，为涡线的涡量，如图6所示中的涡核区。这个方程左边表示涡量的随体导数（或者涡量输运率），右边第一项表示流场的不均性引起涡管的拉伸和弯曲变形，右边第二项表示涡管的粘性扩散。如果设流体粘性系数为零，则可得到理想不可压缩流体在有势质量力作用下，亥姆霍茲涡量方程。

现来进一步讨论上述方程中各项的物理意义。例如，方程中包含的项

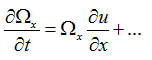
表示涡管的轴向拉伸变形（涡管轴线拉伸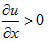，使涡量增大，截面减小），引起涡量的变化率。方程中包含的项

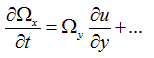
表示涡管的剪切作用，引起涡量的变化率。方程中包含的项

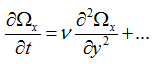
表示涡量的粘性扩散项。

  图6  旋涡