Ansys Workbench工程应用之——结构非线性(上):几何非线性(3)——屈曲
1 屈曲的概念
结构失稳即屈曲,最常见的便是压杆失稳现象。压杆稳定示意图如下,在稳定点之前,支反力呈线性增长,逐渐达到一个极值,之后支反力降低,这个极值便是屈曲极限。屈曲极限往往远小于材料的屈服强度,屈曲分析的目的在于找出结构的屈曲极限,分析出结构的安全载荷、或对结构进行相应优化设计提高屈曲极限。
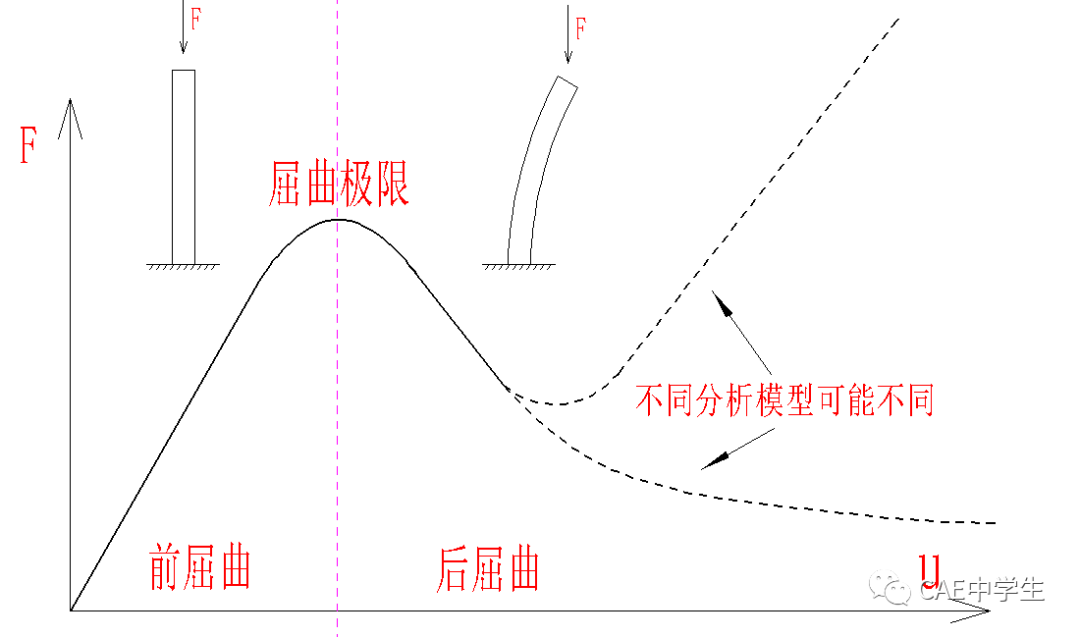
分析屈曲有两类方法,一类是线性特征值屈曲,用于计算理想线性屈曲极限,一类是非线性分析,用于计算零件因初始缺陷、材料、几何、接触等引起的非线性屈曲,而非线性分析又分为前屈曲分析和后屈曲分析。很多结构设计是以理想线性屈曲极限除以一个安全系数作为设计依据,但是如果要探究结构的实际屈曲极限,有必要进行非线性屈曲分析。

特征值模态只是结构的线性特征,是结构在受荷载情况下能量最小的变形模式,不是真实变形。最终采用大变形方法计算得到的结果才是结构真正的破坏状态。

2 线性屈曲
在Ansys Workbench中,进行线性屈曲分析的是特征值屈曲模块。
线性特征值屈曲分析通过提取线性系统的刚度矩阵的奇异特征值,以获得结构临界失稳载荷以及失稳模态。
线性特征值屈曲分析不考虑初始结构缺陷与非线性因素的影响,计算较快,计算精度不如非线性屈曲,特别是对于复杂模型。但是计算的特征值对结构稳定性评价有一定帮助,例如,求解出密集排列的负载乘数,则表明该结构对初始缺陷敏感;求解出稀松排列的负载乘数,则表明该结构对初始缺陷不敏感。

需要强调的是,线性特征值屈曲计算得到的失稳模态变形结果,并不是真实结构失稳后的结构最大位移。更具体地说,通过特征值屈曲,计算出来的最大变形通常在1mm左右,并不代表这时候失稳变形就是1mm左右,特征值屈曲的变形计算结果只能作为失稳方式和这种模态下各处的相对位移变化大小。所以我们应该关心的是各阶屈曲极限(负载乘数),和这种模态下的屈曲方式。

第一阶失稳是最常见的失稳方式,在线性特征值屈曲中,通常只需要计算第一阶屈曲极限。
实例1 对1000mmx1000mmx10mm的薄板,使用默认结构钢材料。一边固定,计算另一边施加多少N的压力会使薄板失稳。

Step1 建立项目分析流程
进行线性屈曲计算之前首先必须对模型进行静力结构计算,建立“静力结构Static Structural——特征值屈曲Linear Buckling”的项目分析流程。在WB主页面的工具箱中将静态结构到项目区,再将特征值屈曲到刚才建立的静态结构的求解栏目,如下图。

Step2 建模
右击静态结构的工程结构——新Dsign Model模型,使用DM建立基于草图的曲面,长宽1000mm,厚10mm。
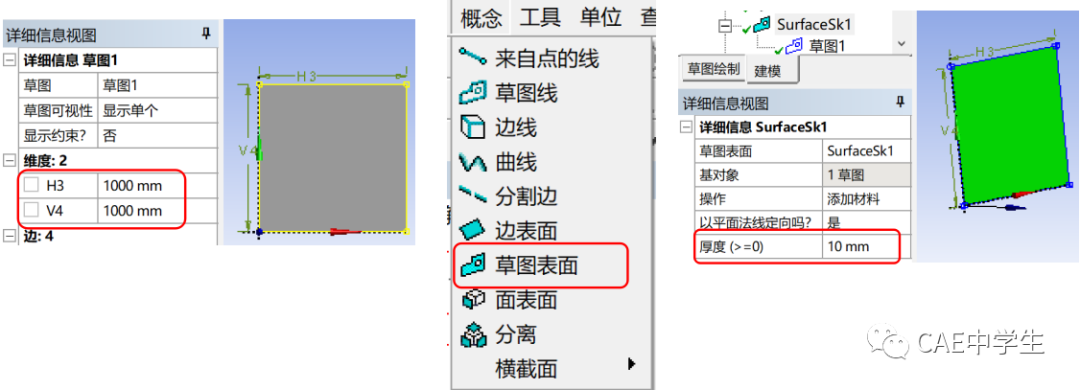
Step3分析前处理
进入Machaniacl界面,为模型赋予WB默认的结构钢材料。分析设置中的大变形不要打开。
划分网格:使用尺寸=50mm划分网格。
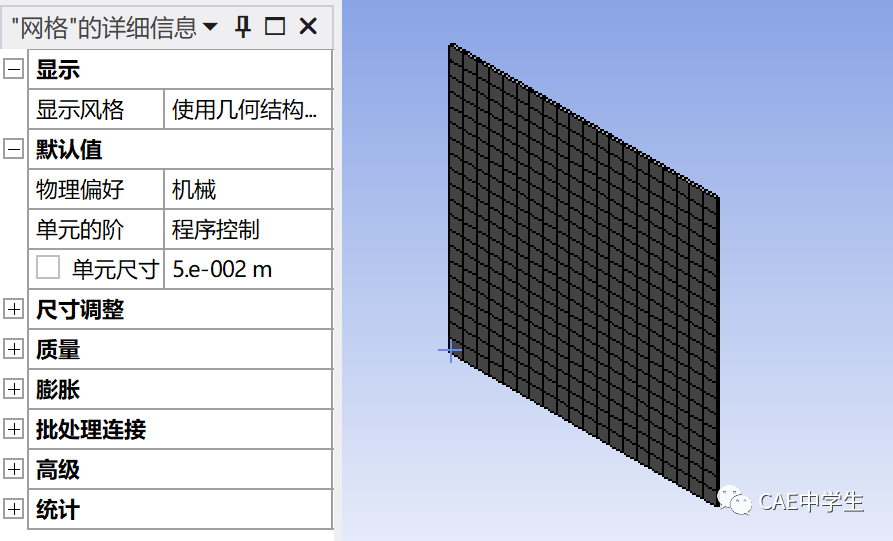
施加边界条件:固定一边,对另一边施加1N的压缩方向的力。

Step4特征值屈曲设置
在特征值屈曲菜单下,点击分析设置,将最大模态阶数改为6,表示只计算前6阶失稳形态。对于线性屈曲,一般只关心第一阶失稳,此处计算6阶是为了分析模态分布是否密集,为非线性计算做准备。

Step5求解与后处理
点击Solve求解。
点击结构树中的求解Solution,在右侧下方出现图表,显示屈曲安全倍数。本例第一阶计算值为43549,表示如果施加的力为算例中的43549倍将产生屈曲,即屈曲临近力为43549N。

第一阶变形方式如下图。

注意:特征值屈曲分析本身是一种线性分析,但是可以静态结构的预分析中设置材料非线性(如超弹性、塑形)、几何非线性(打开大变形)、接触非线性等,使屈曲分析结果更精确。例如上例中的静态结构预分析中,我们打开大变形,屈曲分析结果如下。

计算后跳出提示信息如下

第一个提示信息意思是屈曲分析设置中我们使用了默认的“保持预应力载荷=是”的选项(如果改为否,则需要我们在屈曲分析中添加节点力、节点压力、节点位移等边界条件)。
第二个提示信息意思是 屈服力=静态结构中施加的载荷*(1 倍数)。
计算值为43548,则表示:屈曲力=1N*(1 43548)=43549N。

3 非线性屈曲
非线性屈曲包括基于初始缺陷的非线性屈曲,和塑形行为、接触、大变形响应的非线性屈曲。非线性屈曲考虑了历史加载过程、各种非线性因素、初始缺陷等因素,分析结果更接近真实结构的屈曲极限。
非线性屈曲分为前屈曲和后屈曲,加载方式可以是载荷,也可以是位移。载荷加载一般用于前屈曲分析。在应用了非线性控制——稳定性控制和重启后,载荷加载也可计算后屈曲。位移加载即可用于前屈曲,也可用于后屈曲。
理想的前屈曲计算的位移—载荷图是这样的。屈曲极限即算得斜率为0时的载荷。由于计算前对屈曲的值是未知的,所以一般加载的载荷>估算的屈曲极限,所以斜率收敛为0后载荷将继续增加。

但是实际计算中,可能因为各种原因,特别是牛顿法的自身特性决定,斜率很多时候不能收敛为0,而是下图这样的,此时我们可以取斜率趋近于0而且突变的点作为屈曲极限。

基于初始缺陷比例因子问题
非线性屈曲计算常用的方法是基于初始缺陷或基于微小扰动的计算,他们能比线性特征值计算得到更加准确真实的屈曲极限载荷。
基于初始缺陷的屈曲计算流程是这样的:先建立特征值屈曲流程,再添加一个静态结构,继承材料的工程数据,然后将特征值屈曲的B6(求解栏)拖入到静态结构的C4(模型栏),便形成了一个基于初始缺陷的屈曲计算流程。

完成了流程建立后,需要定义初始缺陷。初始缺陷主要是指几何方面的缺陷,比如零件在生产、运输、安装调试过程中的变形,使得零件的形状与理想形状之间产生的差距。
在这套流程图中,定义初始缺陷很简单。右击流程中的B6(特征值屈曲的求解栏)——属性,在属性中设置基于特征值屈曲的第几阶模态形状的多少倍比例因子来进行计算。

很多书上对这个比例因子介绍的比较模糊,导致大量初学者望而生畏,图惜也很久没搞懂这个比例因子根据什么来设置。后来明白了才知道很简单,是想得太复杂了。很多时候,我们没搞懂一件事情,可能往往只需要别人提一句,就能茅塞顿开。此处图惜说一个公式,大家一看就懂了。
比例因子=零件实际形状÷特征值屈曲的模态形状。
再用实例解释下这个公式,一块矩形板第一阶屈曲模态如下。

现在,我们基于这个模态的变形形状,把它放大100倍,作为非线性计算的初始缺陷模型。按照上文设置,模式(翻译错误,应该为模态)=1,比例因子=100。

然后我们刷新B6,再进入到C项目中的Mechanical中查看零件的初始形状如下,可以发现,这个算例中的零件初始形状,是在屈曲分析的第一阶模态形状基础上放大了100倍。

明白了放大原理外,还有一个难点,就是到底比例因子取多少合适,这个问题就好比我吃饭应该用多大的碗,因为它没有一个标准答案。此处图惜可以给一些建议,首先我们应该忘记上图中的100,因为实际初始缺陷不可能这么大,对于机械制造行业,一些书本一来就整出10倍20倍的初始缺陷,那也是不合理的,在工厂里,打螺丝的小哥生产出变形这么大的零件,估计明天就得卷铺盖走人。
不同情况下,我们考虑的比例因子取值依据是不同的,比如细长压杆,主要失稳是第一阶压杆失稳,它失稳的模态形状是下图这样的,那么对它影响最大的初始缺陷就是杆的直线度。

再比例压力容器、压力管道外表面受压时某阶屈曲变形是下图这样的,那么对它影响最大的初始缺陷就是圆柱度、圆度等。

具体某个零件,只要生产、运输、安装调试完成,那么它的初始形状基本就确定了,一般质量部门会对它进行检验。比例某一批次压杆生产完成后,轴心直线度ф0.1~ф0.6mm,按照最恶劣情况计算取轴心直线度ф0.6mm,而在特征值计算中,第一阶屈曲位移主要变形为压杆的轴心弯曲,如果特征值最大位移1.2mm,那么初始缺陷我们可以取值为0.6/1.2=0.5。
还有一种情况,产品还没有开始生产,结构分析部门需要辅助设计部门对某零件进行屈曲分析,以便考核设计是否合理。对于这种情况,没有实际产品可供质量部门检验,那就需要查询图纸对形位公差和尺寸公差的要求,如果图纸也还没有出,那么就查本公司、或者本行业、或者国家的相关制造验收的规范,一般来说优先级是这样的:企业标准>行业标准>国家标准。常用施工/制造规范有《GB50755钢结构工程施工规范》,《GB50205钢结构工程施工质量验收规范》等,比如GB50205规范中有这样得规定

比如我们关心的屈曲模态为弯曲,那么最大初始缺陷就看弯曲矢高L/1500且不大于5mm,L为钢管长度。L/1500(且不大于5)÷某阶特征值屈曲最大位移量就是我们需要得比例因子。因为很多时候各阶特征值屈曲最大位移≈1mm,所以很多地方也直接取比例因子=L/1500(且不大于5),您在一些书上看到的实例中,超过7.5米管件比例因子取5就是这么来的。
不同的初始缺陷比例因子,计算结果也是不同的。初始缺陷比例因子越小,越不容易收敛,载荷达到屈曲极限附近的变化约激烈(圆角小);初始缺陷比例因子越大,越容易收敛,载荷达到屈曲极限附近的变化越缓慢(圆角大)。

实例2 使用非线性方法求解上例的屈曲极限
方法1(推荐)基于初始缺陷的非线性屈曲
Step1建立项目分析流程
在前面特征屈曲算例基础上,新建静态结构项目C,拖动B2至C2,B6至C4,此时C项目会自动删除几何结构一栏,建立了下图流程。

右击B6栏——属性,设置比例因子、模式(翻译错误,应该为模态)等。
初始缺陷比例因子=0.1,模式=1,即以第1阶特征值屈曲计算得到的变形的0.1倍作为初始的有缺陷的模型。
右击B6——更新。若不更新特征值算例的求解项目,将无法进入C项目的Mechaniacl程序。若提示更新错误,是因为文件未保存或保存了中文路径。

Step2边界条件的加载
双击C3进入Mechanical,材料、模型、接触、网格等数据会传递到C项目中,但是用户应检查接触是否有传递遗漏。
边界条件与特征值屈曲算例中相同设置,但是力需要设置为比特征值屈曲计算的屈曲极限稍大的力,此例设置为45000N,即当然也可以不设置力而设置位移。

Step3分析设置
首先开启大变形。

其次设置载荷子步,此例暂时设置初始子步=50,最小子步=40,最大子步=300,若遇到收敛问题再将相应值调大。

最后设置输出控制,存储结果在=所有时间点上。

Step4求解与后处理
点击求解Solve,非线性计算比特征值屈曲计算将花费更多的时间。
添加变形结果如下

添加支反力结果:右击特征树中求解——插入——探针——反力。
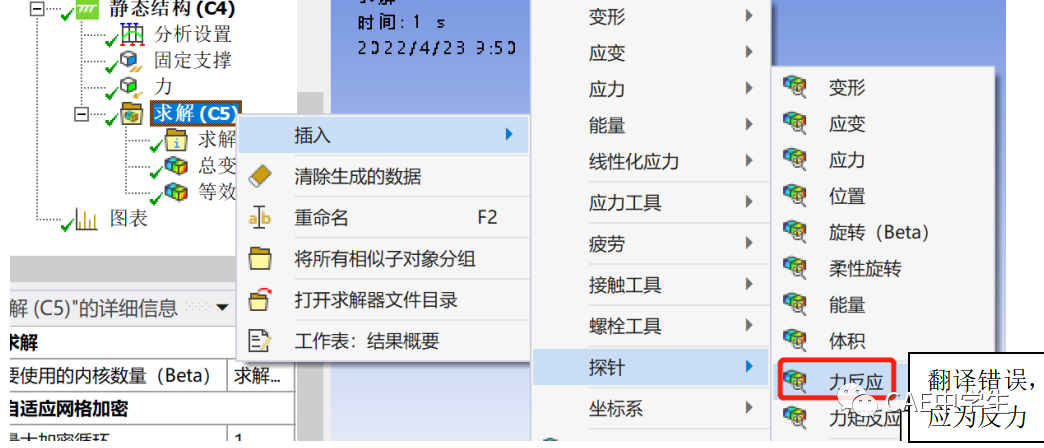
设置反力的属性,然后评估结果
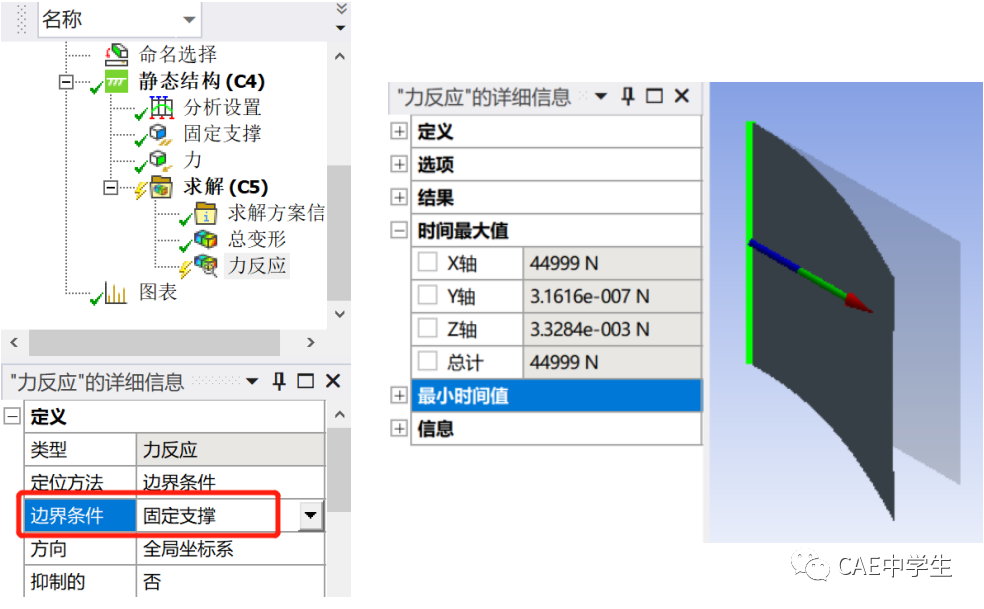
要想直观形象地查看屈曲极限,可以通过建立支反力——最大位移的图表结果来实现,方法如下:
选**征树中的求解,在标题栏选择求解——图表。

在属性中设置:定义选择中按住Ctrl同时选择结果中的总变形和反力。X轴设置为总变形(Max),读者也可设置为X方向的反力,道理是一样的。不显示时间轴、最小总变形、Y方向反力、Z方向反力等,计算结果如下图。
可以从结果中看到,计算到第38子步,载荷为42300N前,零件刚度缓慢降低,变形缓慢增长,计算到42300N后,零件刚度突然变小,位移急剧变大,说明屈曲极限约为42300N。

方法2(不推荐)基于微小扰动的非线性屈曲
非线性屈曲还有一种更简单的计算方法,无需计算特征值屈曲,直接使用静态结构的非线性功能计算,在加载压力之外,还需加载一个促使屈曲发生的微小横向扰动力。
这个微小力取多大的值不好评估,所以一般不推荐采用这种方法。
Step1建立项目分析流程
**上例的第一个静态结构作为本例项目:静态结构D。

Step2边界条件的加载
双击D3进入Mechanical,边界条件与特征值屈曲算例中相同设置,力需设置为比特征值屈曲极限稍大,此处设置为45000N,再设置一个Z方向促使失稳的微小扰动力0.1N。

Step3分析设置
与基于初始缺陷的屈曲分析设置一样,开启大变形。设置载荷子步,此例暂时设置初始子步=50,最小子步=40,最大子步=300。设置输出控制,存储结果在=所有时间点上。
Step4求解与后处理
与上例添加相同的结果,在支反力——位移结果可以比上例更直观第看出突变点,在计算结果中,或许或出现反弹现象,比例下图中,位移达到6.7mm后又突然减小,我们只需要取刚度突变点作为屈曲极限即可。
在第39子步前,位移增量较小,第39~40子步位移增量突然变大,所以取第39子步载荷为屈曲极限,即43425N,与基于初始缺陷的屈曲计算差不多。

本图还可以看出屈曲附近的计算点太少,我们可以重新设置初始子步、最小子步、最大子步,重新计算。屈曲极限算得约为43200N。

大家或许会发现,以上的非线性计算中,我们并没有使用分析设置——非线性控制——稳定性功能。那是因为前屈曲计算一般不需要稳定性控制,在下文得后屈曲计算中,将用到稳定性控制。
后屈曲需要计算出F-u(载荷-位移)图的下降段,以顶点作为屈曲极限,所以计算的值更可信,但是计算量也更大。

非线性屈曲有以下几种计算方法(摘至《ANSYS Workbench 有限元分析实例详解》——周炬 苏金英)

动力学有一定的下降段计算能力,但是无法捕捉跃越失稳。但显式方法可以处理复杂的接触问题,本文不做介绍。
控制载荷加载法由于收敛性问题,只能用于前屈曲,但是在应用了重启和稳定性控制后可以计算后屈曲。
控制位移加载法可以用于前屈曲和后屈曲,比控制载荷加载法更容易收敛,位移控制的缺点是只有在知道施加什么位移时才适用! 比如下图拱梁上施加压力载荷, 而不是集中力, 位移控制不可能使用。对于较复杂的载荷状态, 一般也不清楚施加什么位移。
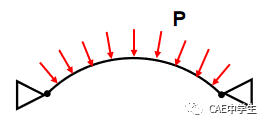
弧长法有较好的下降段计算能力,弧长法和完全牛顿法的区别在于, 牛顿法在每一子步使用一个固定的外加载荷矢量(F),而弧长法在每一子步使用一个可变的载荷矢量(λF),通过强加弧长迭代以得到沿与平衡路径相交的圆弧收敛,能够获得经历零或负的刚度行为的结构的解。

实例3 使用非线性后屈曲方法求解圆弧板的屈曲极限,由于本例圆弧板有屈曲趋向,所以无需设置初始缺陷,使用非线性静力学模块计算即可。
方法1 控制载荷加载法
Step1 建立算例与模型。
新建静力学算例,使用DM创建1/4圆弧曲面模型,圆弧半径R25,曲面拉伸长度50。

Step2 对称处理。
退出DM,进入Mechanical中。右击模型(A4)——插入——对称。

属性设置如下:重复数量2,类型为极坐标对称,对称方法为一半(如果选择全部则为圆形阵列),坐标系设置为全局坐标系,在全局坐标系使用极坐标功能时,Z向将转换为轴向。ΔR=0(径向偏移0),ΔY=0(轴向偏移0),Δθ(切向)设置为90°。注意,Δθ=90°或270°表示沿YZ面对称,Δθ=0°或180°表示沿ZX面对称

使用默认参数划分网格。

Step3 边界条件设置。
在圆弧上边线施加沿Y负方向的2000N的力(别问2000怎么来的,估算比屈曲极限稍大的值,或者先整个特征值屈曲计算,或者慢慢试出来的,不一定用2000,用其他值也许,读者可以自己试试),再限制此边线X和Z方向的位移为0,Y方向自由。圆弧下边线设置简支约束。

Step4 分析设置。
打开大变形。
设置子步如下:

(3)重启控制设置如下,在每一个子步都保留重启点,完成计算后也保留全部重启点。

Step5 初次求解。
点击Solve后开始计算,由于不收敛原因,计算将报错。
与上例一样添加总变形、约束处反力结果,再添加F-u图形,F设置为Y方向的支反力,u为最大位移或者Y方向的位移均可。从计算结果能看出第148子步之后出错。
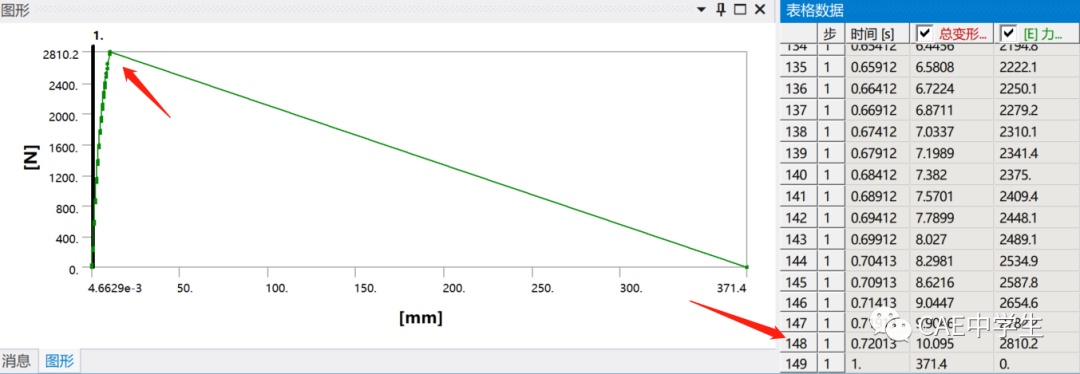
Step6 稳定性控制。
在分析设置——非线性设置中将稳定性设置为常数,方法=能量,能量耗散率默认1e-4,稳定性极限默认0.2。

屈曲极限之后,结构刚度突变小,很小的子步力导致很大的位移,添加稳定性后,可以使屈曲极限之后的位移突变减小,有利于计算收敛。如果遇到不收敛,可以开启并调试稳定性中的能力损耗值(或阻尼值),默认未1e-5~1e-4,是一个很小的值,可以逐渐调试增大这个值,促使收敛。
稳定性选项详解:
程序默认不开启稳定性。用户可以设置的选项有关闭Off、常数Constant、减少Reduce。

常数表示在加载过程中,能量耗散率或阻尼系数不变。减少表示在加载过程中,能量耗散率或阻尼系数逐渐减小,直到在载荷步长结束时减小为0。设置为常数或减少后,需要进一步设置具体参数:

方法:能量表示以能量耗散比率作为控制要素,默认耗散比1e-5~1e-4,用户可以输入0~1之间的值。阻尼表示以阻尼系数作为控制要求,此时需要输入>0的阻尼系数。
激活第一个子步后有3个选择项:否(默认)、是、在非收敛上(On Non Covergence)。分别表示在第一子步是否激活稳定性控制,在非收敛上On Non Covergence表示如果达到最小允许的时间增量后,第一步仍然不收敛,则在第一步激活稳定性控制。
稳定性力控制极限默认0.2,用户可输入0~1之间的数字。
Step7 重启动。
从上文可知,不收敛在第148子步,我们不能从147子步重启,否则还是不收敛。此例我们从第120子步重启。

位移时间历程结果如下

点击Solve,程序便从第120子步开始重启计算。如果还是不收敛可以将稳定性设置中的能量耗散率适当调大。计算的F(Y向)-u(最大变形)结果如下。可见屈曲极限为1404N。u的结果也可以通过在结果中插入用户自定义结果abs(uy),F的结果也可以通过在结果中插入用户自定义结果abs(fy),abs()表示取绝对值。


方法2 控制位移加载法
模型同上,将向下的载荷改为向下的52mm位移。

使用位移加载时,一般不设置稳定性控制也可计算出后屈曲,如果遇到不收敛情况,用户再选择性地添加稳定性控制。此例关闭稳定性控制。
计算的F-u结果如下。屈曲极限为1438.5,与方法1相近。

方法3 弧长法
边界条件与方法1一样,载荷为2000N,在边界条件中添加command命令。并输入以下代码:
nsubst,100 !100个子步
arclen,on,5,0.005 !弧长法,打开,最大弧长系数5,小弧长系数0.05。
最大弧长=5*2000/100=100N,
最小弧长=0.05*2000/100=0.1N.
arctrm,u,52,ntip,uy !弧长法终止准则,位移,52,以ntip节点集位移为准,uy方
向。即当ntip节点集y方向的位移≥52时结束计算。
更多应用请在Ansys帮助文档中搜索Arclen。

使用弧长法必须关闭线搜索(WB默认关闭)、自动时间步,收敛准则不能基于位移收敛。
分析设置如下
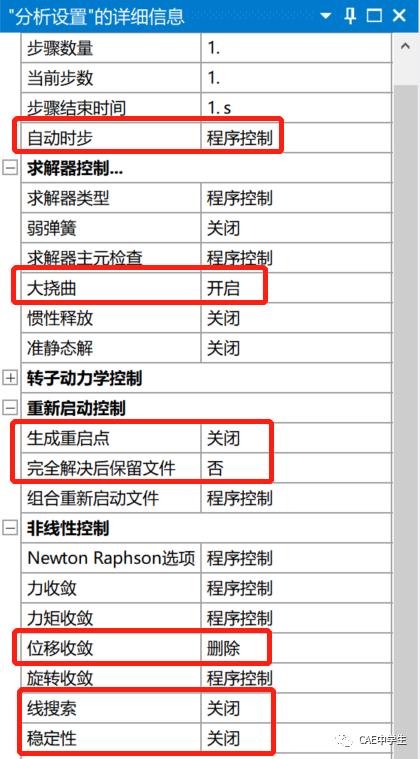
计算结果如下

4 写在最后
实际工程中,很少有这么简单的屈曲计算,更多的是压力容器失稳问题、钢结构失稳问题等,本文只在抛砖引玉,由于图惜水平有限,文中难免纰漏百出,敬请指正批评。
图惜第一次看到这个屈曲F-u曲线时,感觉特别像心里鸡汤中的自信心——知识积累曲线,你看它们多像啊。

还真的是学习的必经之路,在学习过程中,盲目自信不可怕,妄自菲薄也不可悲,只要不放弃,穿越了狂妄之峰,踏过了绝望之谷,终究能找到真理之门。
虽然图惜断断续续写读书笔记,但是还处于不知道自己不知道的阶段,看到读者们千奇百怪的问题,才生也有涯而学也无涯,才知道自己是盲目自信。所以一些问题图惜真不是不回答,是真不知道,请大家多多见谅。
参考文献:
[1]《Ansys Workbench有限元分析实例详解》——周炬、苏金英
[2]《Ansys Workbench工程实例详解》——许京津
[3]《ANSYS Mechanical 结构非线性系列课程》——安世亚太苏睿
[4] ANSYS 2022帮助文件





