【技研】车身环状框架结构断面正向轻量化设计
车身概念设计为车身设计的前期阶段,此阶段确定了车身详细设计的结构形式和60%以上的成本。其中,对车身主断面进行反复优化迭代以减少设计缺陷为车身概念设计的主要工作。
承载式车身为现代汽车的常见结构,属于空间框架结构,需承载各种复杂工况下的载荷。刚度是影响车身承载能力的重要因素,与汽车操纵稳定性、舒适性、NVH 等性能直接相关。美国高速公路安全管理局(National Highway Traffic Safety Administration,NHTSA)发布的2019 版美国新车评价规程(US New Car Assessment Program,US-NCAP)中,侧碰占总体星级评价20%的比重,该工况分为可变形移动壁障(MDB,12.5%)与柱碰(POLE,7.5%),由车身A 柱、A 柱上边梁、B柱等构成的车身前门环状框架结构(本文简称车身前门环)为车身发生侧碰时抵御变形的主要结构。
国内外学者针对车身碰撞及刚度性能进行了深入的研究。张维刚[1]等人单独研究了B柱变形模式对侧碰的影响,但没有研究刚度优化分配下碰撞性能的影响;雷飞、陈新[2]等人研究了车身板厚、材料对侧碰性能的影响,但关于其对车身截面的形状以及车身刚度性能的影响缺乏研究;Kojima 和Nishigaki[3]提出了一阶分析(First Order Analysis,FOA)的概念,基于FOA思想开发了用于概念设计的车身建模与CAE分析程序。
本文在深入分析主断面库作用的基础上,研究基于主断面关键坐标及板厚的主断面属性控制方法,从而探讨满足弯扭刚度及侧碰工况约束条件下车身前门环主断面属性的优化途径。
前门环结构主断面优化设计主要步骤如图1所示。
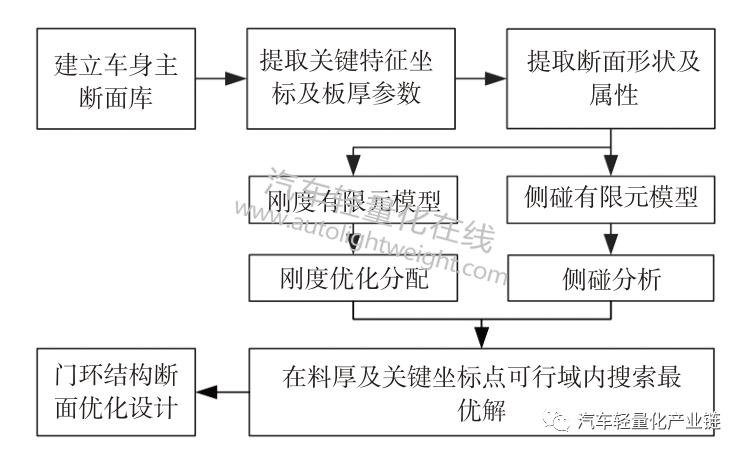
图1 前门环结构主断面优化设计思路
3.1 主断面库的建立
主断面贯穿于车身设计的始终,决定了车身钣金与周边零件的匹配以及密封性要求。承载式车身断面的形状与尺寸对车身框架的刚度及碰撞性能尤为重要。主断面库的建立可以提高车身研发效率,同时利于产品研发经验积累。图2所示为门环主断面位置示意。
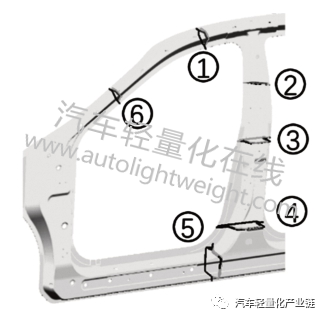
图2 门环主断面位置示意
车身主断面设计时应考虑冲压、焊装、涂装的工艺要求,兼顾造型约束、尺寸、密封性能以及总布置等方面的要求。图3所示为某车型A柱及B柱锁扣处断面,可知外板形状主要由造型、密封条、门运动包络、A柱障碍角等决定,内板形状取决于内部空间和人机头部包络要求。
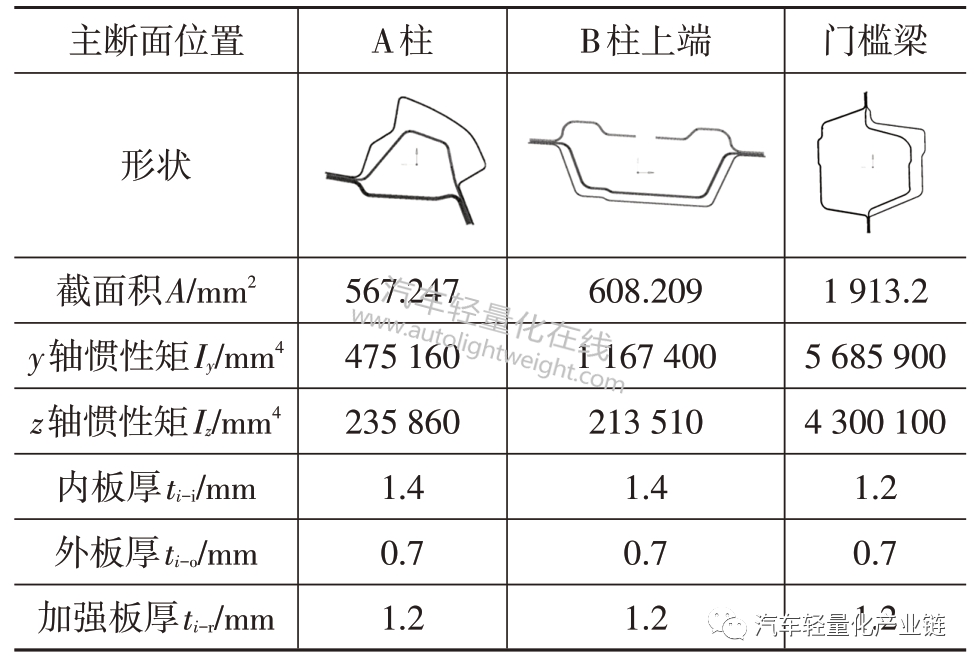
主断面库不仅包含主断面形状、尺寸,还包括主断面的位置、属性(面积和惯性矩)、内外板与加强板的位置关系、板材厚度等参数,本文建立的主断面库如表1所示。
3.2 主断面属性计算方法
为了便于断面形状及板厚的快速优化迭代,本文利用分段法计算主断面属性,由弗拉索夫薄壁杆件理论可以推导出主断面实体部分面积和惯性矩的计算公式:
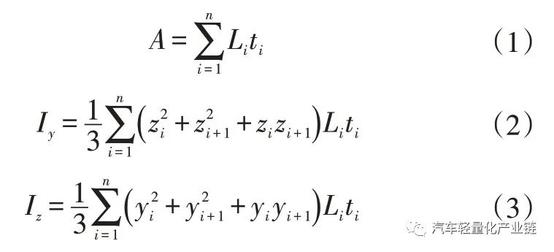
式中,Li、ti分别为区段i的长度和钣金料厚;yi、zi为区段i的y轴、z轴坐标;n为区段数量。
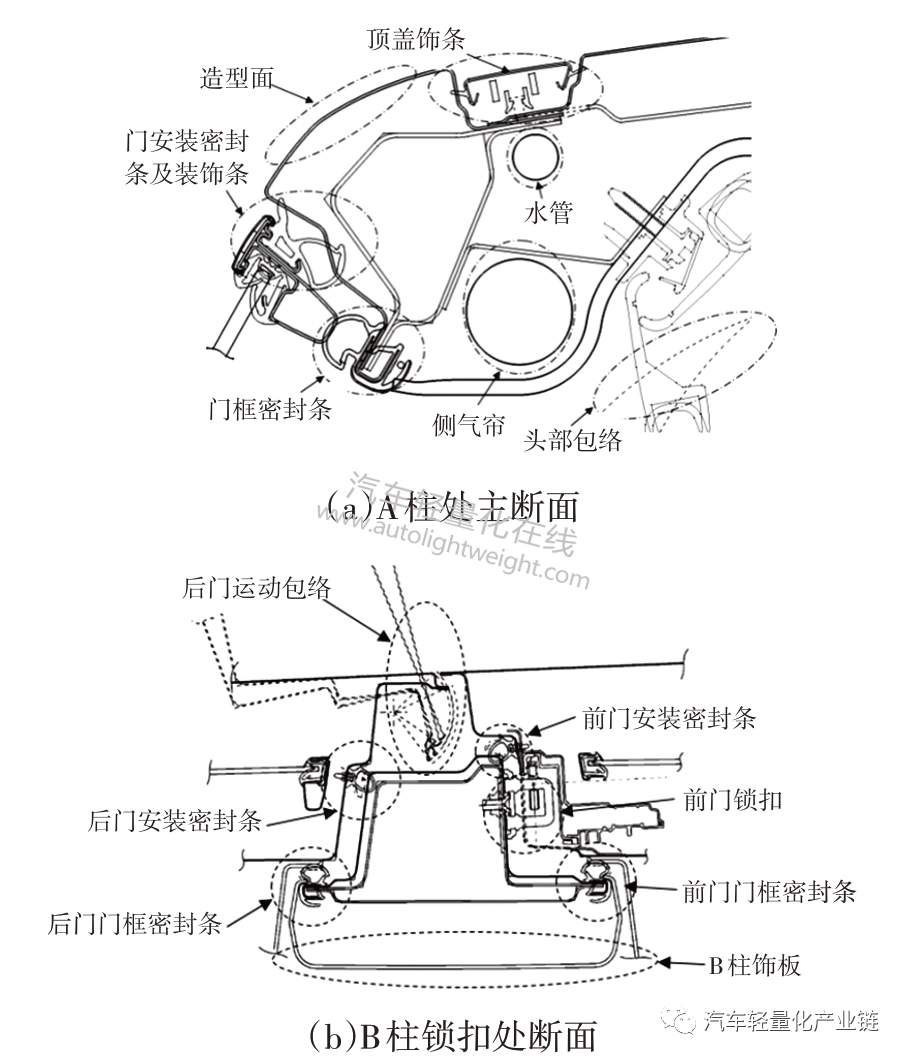
图3 主断面周边布置
表1 主断面库实例
4.1 弯曲刚度分析工况
采用门槛梁加载方式进行白车身弯曲刚度分析,车身前端约束前左、右减振塔大孔中心,车身后端以弹簧支座中心为支撑约束点,车身前端左、右侧约束为DOF23,后端左、右侧约束为DOF123。左、右侧门槛梁于前、后约束中间位置各对称施加弯曲载荷F=1 kN,如图4所示。

图4 白车身弯曲有限元模型
计算左、右侧加载点处门槛梁的z 向变形量,分别记为Wl、Wr。则白车身的弯曲刚度k为:
![]()
4.2 扭转刚度分析工况
采用两侧力加载法进行白车身扭转刚度分析,前端在防撞梁中间位置(y=0 平面上)增加1 个DOF3 约束,后端左侧约束为DOF123,右侧约束为DOF13。前左、右减振塔大孔的中心各施加左右对称、方向相反的力F=1 kN,以产生扭矩,如图5所示。

图5 白车身扭转有限元模型
计算左、右侧加载点处门槛梁z 向位移,分别记为Dl、Dr,左、右测量点间y向间距为Ly,则车身扭转角α为:
扭转刚度kt为:
![]()
4.3 侧碰分析工况
根据2018版中国新车评价规程(C-NCAP)的侧面碰撞(MDB)试验要求,建立整车侧碰有限元模型,如图6所示。移动台车前端加装可变形吸能壁障冲击试验车辆驾驶员一侧,移动台车质量为950 kg。移动壁障行驶方向与试验车辆垂直,碰撞速度为![]() km/h,移动壁障的纵向中垂面与试验车辆上通过碰撞侧前排座椅R 点向后250 mm处的横断垂面之间的距离应在±25 mm范围内。
km/h,移动壁障的纵向中垂面与试验车辆上通过碰撞侧前排座椅R 点向后250 mm处的横断垂面之间的距离应在±25 mm范围内。

图6 碰撞分析有限元模型
5.1 优化设计变量
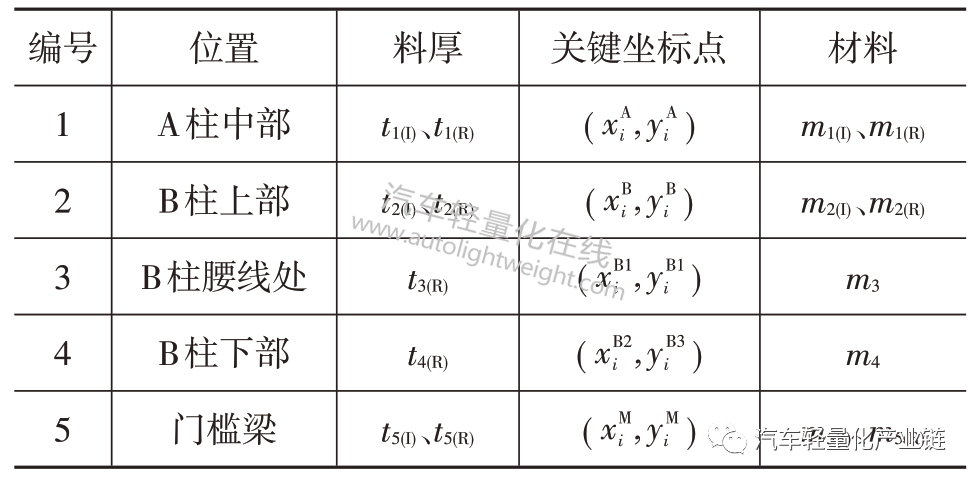
根据车身刚度灵敏度分析可知,5 处位置主断面对刚度的灵敏度较大,即A 柱中部、B 柱上部、B 柱腰线处、B 柱下部和门槛梁,因此选取对断面属性影响较大的料厚、关键点坐标作为设计变量。其中料厚t∈{0.8 mm,1.0 mm,1.2 mm,1.4 mm,1.5 mm,1.8 mm,2.0 mm},属于离散变量,关键点坐标需满足冲压角度、焊装空间要求,为连续变量。在侧碰分析中需引入材料参数,可从材料库中选择340LA、420LA、590 DP、780 DP、980 DP 5种高强度钢及热成型钢HF1500,为离散变量。
本文以A 柱为例说明关键点坐标的选取规则。A柱外板形状主要由造型、密封条、门运动包络、A柱障碍角等决定,内板形状取决于内部空间布置以及人机头部包络要求,因此可取加强板形状控制点作为A柱处断面的关键坐标点,如图7所示。

图7 A柱处断面关键坐标点
图7 中,ti(I)、ti(R)分别为位置i 处内板和加强板的料厚,由于车身侧围外板较薄,对车身性能影响较小,为了减少设计变量数量,将外板的料厚设为固定值。B柱内板料厚设为一致,设计变量的选取如表2所示。
表2 优化设计变量
5.2 约束条件
5.2.1 刚度约束条件
根据4.1、4.2节所示弯扭静态刚度分析工况,本文以弯扭刚度作为约束条件:k≥18 000 N/mm,kt≥16 000 N·m/(°)。
5.2.2 侧碰约束条件
CAE 分析可知,以B 柱侵入速度vB与侵入量yB作为碰撞安全性能的约束条件。本文以满足法规的对标车为研究对象,经仿真分析,B 柱结构对应假人身体部位及各部位侵入速度如图8、图9 所示,本文以上肋骨、中肋骨、下肋骨侵入速度平均值作为B 柱侵入速度约束值,即B 柱侵入速度≤7 m/s,原方案B 柱侵入速度为8.3 m/s。
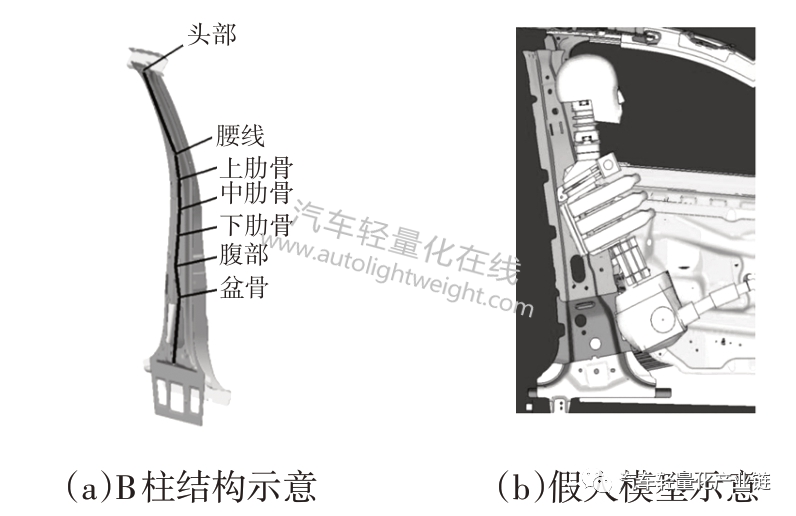
图8 B柱结构对应假人的身体部位

图9 各部位侵入速度
选取对标车腰线至臀部区域的侵入量平均值作为B柱侵入量约束条件,即B柱侵入量≤170 mm,各部位侵入量如图10所示,原方案侵入量平均值为181 mm。

图10 各部位侵入量
5.2.3 优化计算模型
以车身质量m最轻为目标函数,建立优化计算模型:
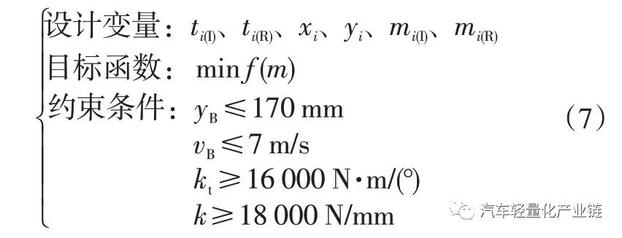
5.3 提取样本点及构建代理模型
本文采用均匀拉丁超立方抽样(Latin Hypercube Sampling,LHS)方法进行样本点的选取,优点是每个因素的设计空间都均匀地划分开,能保证各区域都有样本点,且适合影响因素较多的情况。为保证样本精度和分析成本,本文样本数量为5倍变量数量。
Kriging等是一种距离加权的插值近似方法,其数学模型为:
式中,y(x)为实际模型;f(x)为代理模型;z(x)为修正函数;fi(x)为事先确定的基函数;k为基函数的数量;βi 为回归系数。
代理模型精度与协相关函数关系密切,选取高斯相关方程为协相关函数,任意二点xi、xj 的协相关函数为:
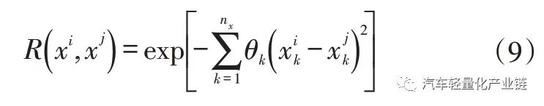
式中,θk为设定的相关参数;nx 为设计变量维度;![]() 在第k个方向的坐标分量。
在第k个方向的坐标分量。
选取决定系数R2 对代理模型的精度进行估计:
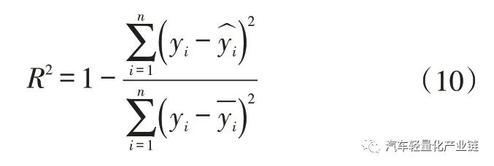
式中![]() 分别为实测值、代理模型预测值、实测值平均值。
分别为实测值、代理模型预测值、实测值平均值。
R2 越接近于1,代理模型精度越高。本文运用Kriging 方法建立设计变量与性能目标之间的代理模型,并通过计算得到B柱侵入速度、B柱侵入量、车身质量f(m)、弯曲刚度、扭转刚度的决定系数R2 分别为0.981、0.980、0.949、0.935、0.977。因此,代理模型精度较高,可用于优化设计。
5.4 优化求解及结果分析
本文所建立的模型为多变量、多约束的非线性优化数学模型,采用冲量梯度下降算法可以有效解决此类问题,随着优化截面数量的增加,为了保证得到最优解的概率较高,个体总数和迭代次数均需设置更大的值,同时可以得到更好的车身轻量化效果,但是会导致计算耗时不断增加,因为目标函数和约束条件需要计算的次数显著增多。为了保证计算效率和优化结果的可靠性,选取表2 中5 个位置的主断面进行优化设计,经过100代梯度算法迭代,耗时约为35 min,如图11所示。通过冲量梯度下降算法对近似模型进行优化获得最优设计变量及设计目标值。
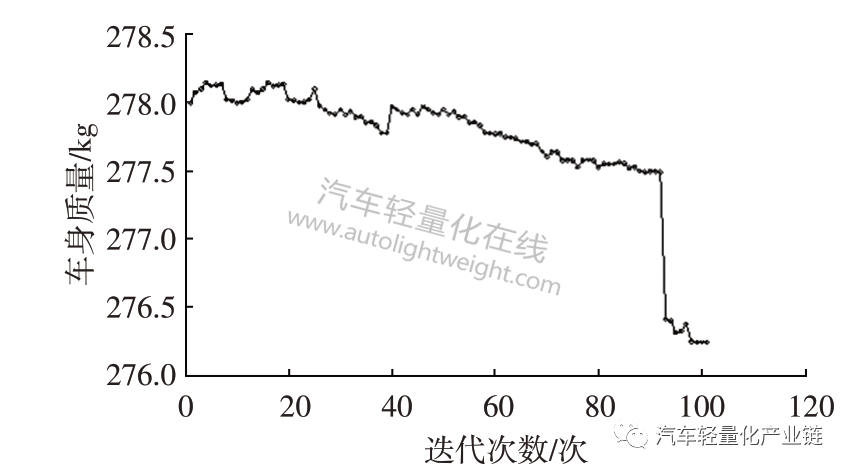
图11 优化迭代过程
设计变量优化结果如表3所示,依据板材规格对优化后的厚度及材料进行选取。
根据优化得到的关键点坐标生成的A 柱断面如图12 所示。
表3 设计变量优化结果

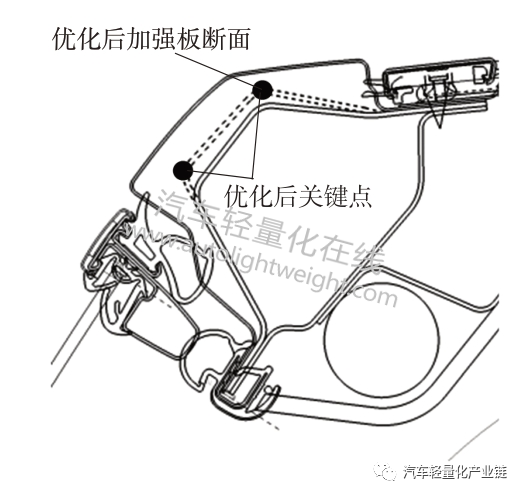
图12 主断面形状优化结果示例
性能参数优化结果如表4 所示,结果表明,优化后有限元模型的弯扭刚度及碰撞性能参数明显高于初始有限元模型且质量更轻。
表4 性能参数优化结果

将优化结果代入碰撞分析有限元模型,初始模型及优化模型变形模式如图13 所示。计算结果表明,优化方案门槛变形减小,B 柱上端没有变形,下端变形位置下移,优化模型的变形模式较为理想。在优化方案的基础上,进行了汽车侧面碰撞实车验证试验,图14所示为侧面碰撞后车身变形量的仿真与试验结果对比。由图14可看出,仿真与试验的变形模式吻合较好,表明仿真模型的准确性较高,同时验证了优化方案的可行性。

图13 初始模型及优化模型变形模式

图14 有限元模型与实车验证对比
本文综合考虑车身弯扭刚度及整车侧面碰撞安全性能,提出了满足目标性能约束条件下车身前门环截面优化设计思路。以车身板厚、材料、形状关键控制点为优化变量,采用均匀拉丁超立方抽样方法进行样本点选取,通过Kriging插值近似方法构造设计变量与性能目标间的代理模型,结合冲量梯度下降算法对优化模型进行迭代求解,最后在车身质量最轻的前提下提升了车身弯扭刚度及整车侧面碰撞安全性能。将优化结果代入碰撞分析有限元计算模型,结果表明,侧碰变形模式较为理想,并通过实车碰撞试验验证了优化方案的可行性。
来源:期刊-《汽车技术》;作者:饶俊威 罗培锋 杨万庆 陈仲泽 周文煜(广州汽车集团股份有限公司汽车工程研究院)




