【JY|土木】失稳你过来,我们谈谈吧。
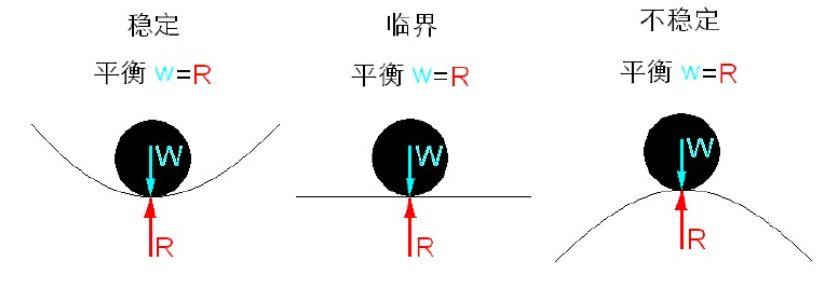
失稳是构件破坏的一种模式,特别在于钢结构中尤为严重,对于因受压、受弯和受剪等存在受压区的构件或板件,如果技术上处理不当,可能使钢结构出现整体失稳或局部失稳或局部与整体的相关失稳。失稳前结构物的变形可能很小,突然失稳使结构物的几何形状急剧改变而导致结构物完全更新换代抵抗能力。。可以认为:构件或结构的失稳破坏是它们内部抗力的突然崩溃,这就是钢结构屈曲现象的特征,不论发生破坏时构件的工作属于弹塑性或弹性工作阶段,破坏特性完全相同。由于结构或构件的失稳破坏比较突然,屈曲一旦发生,结构随即崩溃,因而远比强度破坏危险。
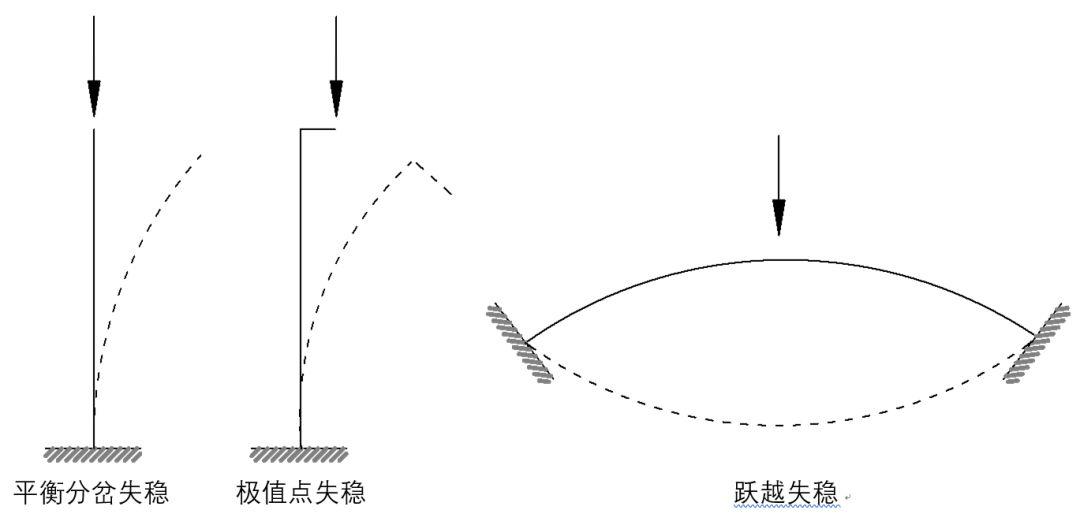

失稳有三种类型:平衡分岔失稳、极值点失稳、跃越失稳!


平衡分岔失稳
典型的结构第一类失稳是指压杆处于随遇平衡的临界状态,如果受到微小的干扰就不能恢复到稳定的平衡状态,结构就失稳了。物体可以处于稳定平衡状态、随遇平衡状态和不稳定平衡状态。压杆由稳定平衡过度到不稳定平衡时所受轴向压力的临界值称为临界力,压杆处于随遇平衡的临界状态,出现了所谓的平衡分叉。所谓“随遇而安”,其实已经“无家可归”了。一遇风吹草动,就失去平衡了。
这种情况,只有在理想的状况下オ会出现。只当一个均匀的细长杆,在受到完全精确的中心受压时,才会出现。注意,对于低屈服应力的短杆,屈曲前有可能已产生塑性变形。但对于细长杆,达到第一类失稳的临界力时,杆件还处于弹性阶段,并未达到强度极限,也没有达到屈服极限,没有出现塑性变形。所以,它不是强度问题,是稳定问题。
第一类失稳时的临界力公式是由欧拉于1714年得到的,通常称为欧拉临界力公式。(公式见材料力学)
在各种不同支承情况下的压杆,例如简支的,而同样长度的悬臂梁计算长度是不同的,失稳的临界力F与是成反比,可见同样长度(度)的简支,其临界力要比是臂果的临界力大4倍,也就是说,简支果比思臂果更不容易失稳。


极值点失稳
第二类失稳是最常见的偏心压杆达到极限值,开始时变形随力的加大而加大,最后,力不加大,变形还在増加,出现力减小而变形仍不断增加的情况。任何现实工程中的压杆,都不会是理想的中心受压,而杆件的几何尺寸也不会理想的对称,还会有先天的缺陷,材料也不会理想的均匀。何况还可能事实上就受到偏心的力。事实上偏心的压杆出现第二类失稳开始是一种几何非线性问题。
压杆还没有达到强度极限,变形就渐渐加大,P-▲效应起作用,P▲=M,▲越大,M越大,而M越大,又导致越大,进入恶性循环。最终导致杆件出现塑性变形,并达到强度极限而破坏。对比一根短粗的压杆,它即使在偏心荷载作用下,也没出现几何非线性变形,只是在压力増大到使杆件压环,达到强度极限,这就是强度问题了。第一类稳定问题在数学上是特征值问题,可以精确地算出来。第二类稳定的临界荷载会小于第一类失稳的临界力,但难以用精确的公式来表达,往往用第一类失稳的临界力去估计第二类失稳的临界力,常用折减材料的弹性模量的方式来适当反映材料的塑性。

跃越失稳
第三类失稳,当力增加到某个临界力时,突然从一个平衡状态跳跃到另一个平衡状态,也称为“跃越”。图如上图显示的结构,当加载到A点时,会突然跳跃到B点,荷载不增加,而变形突然增大。继续加载会沿着BC发展,这叫上升跃越。这种情况会在共、扇平壳体某些形状的帐幕结构出现。在海壁结构和一些特殊的结构(比如航天器上的太阳能板之类)都要防止这种失稳。打个比喻,就像“阳伞吹喇叭”一样。

学生时代中的力学架构设计,受压构件很多也不是截面极限压应力控制,而是临界压应力控制哦!最近力学架构的同学们注意哦~
如果是工程界的攻城狮,那做钢结构的时候要稍微注意下失稳这种破坏模式呀!




