有限元,我们认识世界的工具

有限元方法(FEA)即有限单元法,它是一种数值分析(计算数学)工具,但不是唯一的数值分析工具。在工程领域还有其它的数值方法,如:有限差分法、边界元方法、有限体积法。但由于FEA具有多功能性和高数值性能,使它占据了绝大多数的工程分析市场,其它的因此而被归入小规模应用。
有限单元法已成为一种强有力的数值解法来解决工程中遇到的大量问题,其应用范围从固体到流体,从静力到动力,从力学问题到非力学问题。事实上,有限单元法已经成为在已知边界条件和初始条件下求解偏微分方程组的一般数值方法。
有限单元法在工程上的应用属于计算力学的范畴,而计算力学是根据力学中的理论,利用现代电子计算机和各种数值方法,解决力学中的实际问题的一门新兴学科。它横贯力学的各个分支,不断扩大各个领域中力学的研究和应用范围,同时也在逐渐发展自己的理论和方法。
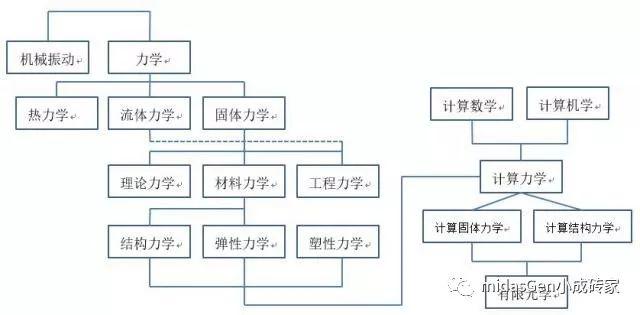
目前在工程技术发展领域内常用的数值模拟方法有:有限单元法、边界法、离散单元法、有限差分法。有限元法(FEA)是其中应用最广泛的一种数值模拟方法。其基本概念是用较简单的问题代替复杂问题后再求解。它将求解域看成是由许多称为有限元的小的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解这个域总的满足条件(如结构的平衡条件),从而得到问题的解。有限元法,是把实际形状的模型用有限个有限单元的**体来建立模型:连续体→离散体。
有限元方法从大的方面说,有如下的研究内容:
物理(Physics)
分析(Analysis)
几何(Geometry)
数值方法(Numerical method)
拓扑(Topology)
可视化(Visualization)
数据结构(Data structure)AI(Aritificial Intelligence)
优化(Optimization)
物理是指研究问题的背景,当年冯康教授、钱伟长教授、胡海昌教授等正是从许多物理背景模型特别是固体力学出发成为一代有限元法大师的,有限元方法应用的领域非常广阔,在固体力学、结构动力学、流体力学、传热学、电磁场、渗流力学等领域发挥着很大的作用,在数学方面,像偏微分方程等也有很大的用途。
分析是指有限元法的数学基础为变分原理,它将物理模型的连续方程、守恒方程等转化为变分形式,变分问题和原来的偏微分方程是等价的,变分原理降低了原来偏微分方程解的连续性要求。变分的不同构造形式衍生出了多种多样的有限元的分枝。
有限元是需要计算具体实现的,实现时首先要划分计算网格,网格从本质上是几何问题,单元的几何形态对精度有影响,因此不可能随便划分单元,像边界元法只需要在边界上划分,它的基础是格林方程,无网格方法只需要在域内部点即可。任何物理场的存在都能视为一种几何结构,单元的**构成了物理场全部的几何信息,涉及到几何问题,自然可以使用几何方法,比如边界表示法等,划分是计算几何的研究内容,目前已经完全做到了几何实体的表示到有限元网格数据的自动转换。
有限元方法在具体计算时最消耗时间,可见数值计算在有限元方法中发挥着可以省工省时的作用,数值计算包括数值积分、线性代数方程求解、特征值求解三方面。后两个是纯算法问题,算法的构造直接影响着计算的效率,经过几十年的研究,诞生了很多高效、稳定的算法,任何好的算法都是计算时间与数据贮存空间的某种“平衡”,数据贮存空间分为内存与外存,省时间的算法占空间,省空间的算法费时间,目前的算法很少有人考虑空间问题;有些算法还考虑了硬件环境,如并行算法,一个值得注意的方向是所谓“Cluster”计算机,它将多种性能的计算机按照一定协议连接,可得到巨大的计算性能,形成所谓的“计算力”,而软件获取费用几乎是免费的。实际上用户可以想象,完全可以利用因特网或局域网上的空闲资源,为密集数值计算服务,比如问题有一亿个自由度,不同用户可以计算出方程中一个小块的某种特性,为解方程所用。目前这在解方程领域还是处女地,但在密码分解、素数分解、素数发现等领域已有实现。“网格”系统是一个新的概念,有限元在其上的应用是一个发展方向。基于完全异步的松耦合系统的算法是绝对是未来几十年的发展方向。

以上四个方面是基本的,下面几点是一些技术因素:
在有限元法中,节点和单元都是需要互相连接的,这可以视为一种拓扑结构,节点的位置可以变化,拓扑连接不变,依照这种拓扑结构甚至能构造出不同物理形状的物体,拓扑连接在结构优化时也非常关键。
无论是物理场还是几何场,人们总希望以某种形象的方式表示它,这样就能研究场的细节,这就是可视化的内容。目前,可视化几乎成了有限元软件的基本要求,从前处理到后处理,用户对可视化提出来非常高的要求,前处理要求和CAD软件无缝集成,后处理则要求和一般的可视化软件集成,这样能大幅度降低开发成本。
数据结构是研究数据贮存和检索的科学,在有限元程序中数据结构可以说是系统分析的内容,系统分析一般用结构化方法或OOP方法,这时要确定模块的功能,甚至要考虑硬件的能力,比如贮存能力,用何种方法贮存“总体刚度”矩阵,像这方面的内容有带宽压缩贮存、稀疏矩阵贮存等,这方面的技术非常成熟,依靠专业的数据库服务器是最佳选择。
AI指人工智能,人工智能是研究逻辑及其推理的科学,有限元法和它结合可以解决求解策略、人工干涉程序计算方向的问题,目前有关人工智能的应用还不多见,商用软件也未考虑此方面的因素,这个领域是广阔的。
优化问题在有限元中有这几个方面的需求,如边界形状优化、最小质量、等强度、等应变、动力学参数优化等,优化问题的特点是变量多(几十/数百),许多实际的优化算法这样多的变量中稳健性还有待提高。优化问题要必须考虑K*U=P、K(U)*U=P(U)、K*U=alpha*M*U方程的灵敏度分析,这是个公认的难点问题,精确计算往往因为计算量太大而用差分法来替代。
未来的一些可能方向:
1)辛问题:将问题转化为辛几何问题,建立基于辛几何场的有限元方法,辛几何是面积守恒的,可望在大尺度时间、大空间尺度等应用领域(如天体、粒子的大范围输运等)发挥作用。
2)斯塔法问题:建立完整的全空间、全时间尺度的有限元方法,以解决两相乃至多相的自由边界问题,如轧钢、南极的冰线移动预测等。
3)发展方程:如孤波问题,孤波是强非线性问题,如果能使用有限元方法比将开阔一个新的领域,目前已有研究,但是高维问题进展缓慢,这类问题目前在光通信领域有迫切应用。
4)计算材料学问题:从原子、分子、团簇等的原始物理方程,研究介质的微观或者宏观性能,是计算材料学的目标,但是微观粒子的互相作用模型大都是强非线性,弱解方程的建立,以及如何与宏观的物理量,如应力等建立有效联系还是很大的问题;计算材料学所涉及的海量计算一般用户难以承受。
5)湍流问题:目前已经有一些较好的方法,如有限体积法等,仍需深入,目前湍流问题实际上根本不是算法问题,而是介质的物理模型问题;人们对湍流的认识可能还受到目前科学技术水平的限制。
6)相变问题、多物理场耦合问题:物质的相变或多场作用产生了特定的行为,相变意味着从一种稳态跃迁或者变化到另一种稳态,描述这种强烈的非线性行为,有限元方法还可能应用吗?在何种尺度上应用?多物理场耦合问题目前热点很多,关键是不同场的作用机理,方程的解耦等研究,单从方法上,原创点不多。
7)分子力学、纳米力学问题:在分子、纳米的尺度上,介质或材料展现了迥异的行为,这是目前的研究热点,目前这类问题还主要是物理问题,有限单元方法只是一种算法、思想;如果科学家们研究清楚了分子之间的互相作用、纳米团聚间的互相作用,才可能到有限元发挥作用的时候。
8)与小波分析结合:“小波”被称为“数学显微镜”,对于时关系统,时间与频率是同一系统的两个不同方面,缩短时间与就能提高频率的分辨率,这种思想可说是“奇妙的”,有些类似有限元中的谱法;受小波法启示,如果在有限元中能够找到一对分辨率彼此消长的物理量,有可能大大提高有限元的应用效率,在有限元中单元的大小与求解精度就是这样一对物理量,还有其它的吗?
9)经济、社会、管理领域:像目前固体力学中的多尺度方法一样,在经济、社会、管理应用领域微观行为及其发展研究非常热,我们想,在一个自封闭的系统内,只要存在两种微观团体的互相作用,互相作用的关系是可以量化的,这种作用能够使得“系统”稳定,耗散最小,能量最低,“系统”演化可以量化,有限元方法就一定能够发生效用。当然这并不排斥其它的解决方法。

在研究有限元方法时,理解解析与数值计算的关系、理解逼近的思想、理解抽象与具体的相互关系,会发现此法是一个方法学集大成者,它不但将多种概念汇聚一身,又衍生出多种多样的研究内容,无怪乎科学家们将它作为20世纪应力力学的最伟大成就之一。
有限元法不是万能的,关键是其思想,它完美的体现了哲学中局部与整体的关系,要解决整体问题,必须先研究局部问题,局部问题研究清楚后,还要研究局部之间作用的关系,然后各个局部在一个统一的坐标尺度下综合,还要考虑整个系统和外部的关系,最后得到全局的特征。这种思想是自然的,符合人类的思维规律,与企图用公理化或者纯解析化的思想来解决问题不同。人类最关心全局的东西,比如宇宙,及它的过去、现在和将来,但要穷极完全时间尺度、完全空间尺度的全局的性能只是人类的“梦想”,并不符合认识论的一般规律,有些时候完全的“穷极”可能会导致“悲观化”。
有限元法不能解决全部的问题,但这种局部与整体的思想加上计算机技术将这种工具发挥的淋漓尽致。早在有限元法创立以前,科学家们就已经有了思想的“雏形”,比如:瑞利-里兹、伽列金等,但因计算工具落后,难能将这种思想发扬光大,当时他们根本无法看到用这种方法解决大范围问题的希望,只能在较小的范围内应用,但确也取得了巨大的成就。
综上,有限元方法是我们认识世界的科学工具。

【免责申明】
文章为转载,版权归原作者所有。如涉及作品版权问题,请与我们联系,我们将删除内容或协商版权问题!内容为作者个人观点,并不代表本***赞同其观点和对其真实性负责。
The End