基于ANSYS Polyflow的逆向挤出模头设计攻略
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 内容稀缺
摘要:内侧灯罩属于复杂截面塑料异型材,目前其挤出模头的设计主要依赖于经验,需要反复试模和修模,使得模具质量难以保证,生产周期长,成本高。
本文采用数值模拟方法对内侧灯罩进行了反向挤出模头设计。首先对内侧灯罩的挤出工艺进行了分析,然后建立有限元模型,利用Polyflow软件进行了模头设计,最后根据仿真结果进行了模具制造,并进行了挤出实验,实验结果表明采用这种设计方法模具只需要较少的修模就能够满足产品的质量要求。这种设计方法对类似的复杂截面塑料异型材模具的设计同样具有着重要的借鉴价值。
关键词:挤出模;有限元模拟;模头设计
一、引言
挤出加工生产过程连续,生产效率比较高,可以在较短时间内满足厂商的大量需求。但在市场竞争日益激烈的情况下,传统的依靠经验的挤出模的设计制造方法需要反复试模和修模,模具质量难以保证,且生产周期长,成本高,已经满足不了当前生产实践的需求。
随着计算机硬件的持续快速发展和数值技术的进步,现在可以仿真、分析、优化有着复杂形状的三维挤出工艺,并考虑了聚合物熔体的非线性和粘弹性行为。Polyflow软件就是其中最常用的模拟软件之一。
Polyflow用于挤出口模设计的数值模拟主要有两种方法:
(1)对于给定口模,可以利用Polyflow来分析不同工艺条件下制品的挤出成型,由此来确定最佳工艺条件;
(2)根据制品的形状,利用Polyflow的反向挤出功能来设计口模。所谓反向挤出是指在口模设计中,为了得到已知的所需挤出制品的形状,来预先设计口模的形状[2]。
国内外研究者已经在该领域进行了广泛而深入的研究。Vaddiraju等人[1]使用Polyflow软件对一个现有模具进行了正向挤出,得到的挤出件外形和实验挤出的相差不大,同时为了进一步提高挤出件的尺寸精度,他们使用反向挤出对模具进行了重设计。
戴元坎等人[3]采用Polyflow软件、Bird-Carreau纯黏性模型对三元乙丙橡胶(EPDM)在简单口型(正三角形、矩形)及其流道中进行了正向挤出过程模拟和逆向口型设计分析,并加工了相应的口模,通过挤出机进行了挤出试验,试验数据与模拟预测结果比较接近,逆向计算所得到的口型比较合理。
数值模拟技术已广泛应用于塑料型材和简单截面异型材的挤出模具设计,而基于三维数值模拟的复杂截面塑料异型材的挤出模具设计技术尚未成熟。本文对一个复杂塑料异型材的挤出工艺进行了分析,并建立数值模拟的有限元模型,利用Polyflow软件进行了反向挤出模头设计,然后用真实的挤出实验来验证其正确性。
二、产品工艺分析
该产品为上海宝山迦南塑料厂生产的日光灯的内侧灯罩,如图1所示,产品材料为透明PC,其具有良好的物理机械性能。该产品对于上表面的表面光洁度,两脚及两侧边的尺寸配合,两侧边的平直度有要求。

图1期望产品的横截面形状
Fig.1 Cross-section of required product
使用产品形状作为模头出口形状进行正向挤出模拟,可以大致的了解产品的变形趋势,如图2所示。主要变形趋势为:上表面有外扩趋势,两侧边及拐角处胀大率过大,两脚供料不足,上表面拐角处夹角过大,两侧边横向尺寸缩小。

图2 产品变形趋势图
Fig.2 Product deformation trend
为了获得期望的产品形状,在进行模具设计时,应着重补偿上表面的外扩以及两脚的供料不足,并平衡料流分布。但由于产品外形非常复杂,影响因素较多,传统的依赖经验的挤出模设计无法准确的进行外形补偿和料流平衡,故而利用Polyflow有限元软件的反向挤出功能进行模头设计,以期获得满足要求的口模外形。
三、反向挤出有限元建模
1、流变模型选择及其参数确定
普通的流动完全可以用质量守恒、动量守恒、能量守恒定律以及流变和热力学方程来描述,其中流变方程包含了给定材料的全部流动性能。
在聚合物加工成型中,常用的流变模型有以下几种:反映粘度对剪切速率的依赖性的Power-law模型,Prandtl-Eyring模型,Carreau模型,Vinogrador-Malkin模型,Herschel-Bulkley模型,以及反映粘度对温度依赖性的Arrhenius模型和WLF模型。
所有的模型都有各自的优缺点,在进行有限元模拟前,必须选择合适的流变模型,并了解模型的建立条件和材料参数的确定条件,以便使分析在给定方法的限制范围内进行。
由于口模流道结构的几何非线性和高聚物的材料非线性。很难直接从上述方程组中求解。为此,必须对问题作适当的工程简化,考虑到塑料挤出过程的具体工艺条件和材料自身特性,作出如下基本假设[7]:
熔体为不可压缩的广义牛顿流体,不考虑其粘弹性; 聚合物熔体在口模中是三维稳态层流流动; 熔体在流道壁上为无滑移流动,即其各个速度分量为零; 熔体在口模内流动为完全发展流; 由于熔体的高黏性,流体惯性力和质量力忽略不计。
在这些假设条件之下,得到熔体在模头流道中的控制方程如下:
连续性方程
 (1)
(1)动量方程
 (2)
(2)能量方程
 (3)
(3) ——速度矢量,m/s;
——速度矢量,m/s; 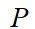 ——压力,Pa;
——压力,Pa;  ——应力张量,Pa,
——应力张量,Pa, ;
; ——物料密度,
——物料密度, ;
;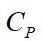 ——物料的比热,J/(kg·℃);
——物料的比热,J/(kg·℃); ——温度,℃;
——温度,℃;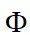 ——粘性耗散热,
——粘性耗散热, 。
。聚合物熔体为非等温的广义牛顿流体,其表观粘度 除了与剪切速率
除了与剪切速率 有关,还与温度T有关。本文中使用的流变模型是Bird-Carreau模型和Arrhenius模型,其中Bird-Carreau纯黏性模型可以在较宽的剪切速率范围内很好的拟合剪切黏度与剪切速率的关系。Arrhenius模型特别适合于用来描述半结晶热塑性材料粘度对温度依赖性的描述。
有关,还与温度T有关。本文中使用的流变模型是Bird-Carreau模型和Arrhenius模型,其中Bird-Carreau纯黏性模型可以在较宽的剪切速率范围内很好的拟合剪切黏度与剪切速率的关系。Arrhenius模型特别适合于用来描述半结晶热塑性材料粘度对温度依赖性的描述。
表观粘度和剪切速率和温度的关系为:
 (4)
(4)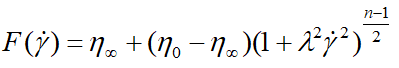

其中  是剪切粘度,
是剪切粘度, 是零剪切粘度
是零剪切粘度  ,
,  是无限剪切粘度
是无限剪切粘度 , 是松弛时间(s),n是非牛顿指数,
, 是松弛时间(s),n是非牛顿指数,  是剪切速率
是剪切速率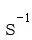 。
。 是活化能,
是活化能, 是绝对零度,
是绝对零度,  是
是  时的参考温度;
时的参考温度;
根据实际生产中使用的透明PC材料的流变性能测试结果,可以拟合得到Bird-Carreau模型参数:
 ,
,  ,
, ,
,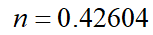
由于进行的是非等温模拟,需要根据三个温度下测得的(零剪切粘度 ),且根据
),且根据 (其中R为摩尔气体常数,E为熔体活化能,A为系数)求得活化能E,即公式5中的
(其中R为摩尔气体常数,E为熔体活化能,A为系数)求得活化能E,即公式5中的 。
。
Arrhenius模型参数:
 ,
, ,
,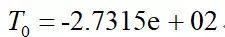
将上述参数代入式(4)(5)(6)可得:

2、有限元模型的建立和边界条件的确定
典型的挤出模流道有3种:一种是等截面的直流道,另一种是变截面的自适应流道,第三种是等截面和变截面的混合流道。从模具入口压力的结果看出,变截面的自适应流道优于直流道和混合流道。但是尽管流道不同,(注:反向挤出得到的)挤出模的出口是一致的。因此,在反向模拟中,仅仅使用直流道的FEA模型来设计挤出模头是足够的[4]。而从加工成本和制造的难易程度考虑,直流道无疑是最好的选择。
图1所示的是内侧灯罩的示意图,由于产品形状对称,我们只取其一半进行研究,网格类型为正六面体,建立如图3所示的有限元模型。该模型是采用直流道的挤出模,有着恒等的口模截面。

Fig.3 3D FEA model and boundary conditions
流动边界条件:
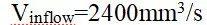 ,充分发展流;
,充分发展流;BC-5:出口,牵引速度为vn=22mm/s,切向力fs=0。
热边界条件:BC-1至BC-5均为220℃。
四、结果分析
1、反向模拟结果
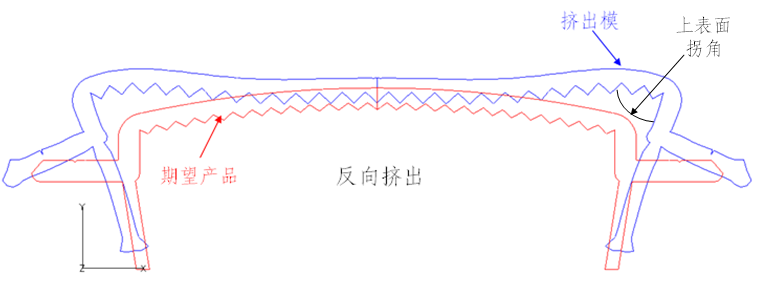
Fig.4 Comparison between die designed by inverse extrusion and the required product

图5挤出模和正向挤出所得挤出件的对比
Fig.5 Comparison between die and the extrudate from direct extrusion
通过反向模拟设计的挤出模和期望产品的外形对比如图4所示。由图可知,反向模拟得到的口模上表面向内凹,补偿了挤出过程中上表面的外扩趋势;根据材料物性(决定挤出胀大)和牵引速度对模具壁厚进行了调整,特别是胀大趋势较为严重的两侧边;供料不足的两脚不仅增大了壁厚,而且在下端添加了一个凸起,进一步增加供料;上表面拐角处的夹角进行了一定程度的缩小;两侧边横向尺寸有所扩大。对反向设计的模具进行了正向挤出摸拟,如图5所示。所得挤出件外形和期望外形基本一致,达到了设计要求。
2、出口截面横向流动分析
由于模头流道内横向流动是模头设计的困难所在[5] ,故而横向流动最小化是优化挤出模头流道设计的主要指标。横向流动最小化可以使无法完全控制的各种工艺波动所造成的流动不稳定对型材尺寸和性能的影响减至最小程度,得到稳定性相对较好的挤出模头[6]。对反向挤出设计的挤出模进行正向挤出模拟,得到模具出口截面的横向速度分布,如图6和图7所示。


Fig.7 Y-direction velocity distribution in the outlet
由图6和图7可知,1位置x方向速度基本为0,而y方向的速度分布导致其截面有胀大的趋势;2位置x方向的速度分布导致其截面胀大,y方向的速度分布导致截面被拉伸从而变薄,而x方向占据优势,2位置总体来说是胀大的;3位置x方向的拉伸和y方向的胀大,综合起来还是胀大为主;
4位置只有轻微的胀大。本文中,反向模拟设计的口模虽然总体上达到了横向流动最小化,但是局部的横向流动仍然存在,可以通过调整模具的结构参数,使得横向流动进一步减少。
3、上表面拐角角度对横向流动影响分析
通过研究口模的结构参数对出口截面横向流动的影响,可以找出最优的口模的结构参数。影响横向流动的结构参数很多,由于上表面拐角处的夹角角度(如图4所示)对于产品外形起着重要作用,故而研究其对横向流动的影响。对改变角度后的模具进行正向挤出模拟,得到各个角度所对应的x和y方向的速度分布,如表1、2所示。
Tab.1 X-direction velocities in the outlet
角度 | -10 | -5 | 0 | 5 | 10 |
最大值 | 3.196 | 3.019 | 3.004 | 3.097 | 3.119 |
最小值 | -3.492 | -3.572 | -3.587 | -3.547 | -3.544 |
差值 | 6.688 | 6.591 | 6.591 | 6.644 | 6.663 |
表 2 出口截面y方向速度表 (单位:mm/s)
Tab.2 Y-direction velocities in the outlet
角度 | -10 | -5 | 0 | 5 | 10 |
最大值 | 3.095 | 2.992 | 2.988 | 3.038 | 3.072 |
最小值 | -2.942 | -3.034 | -3.100 | -3.170 | -3.218 |
差值 | 6.037 | 6.026 | 6.088 | 6.208 | 6.290 |
注:表1与2中逆时针旋转为正,顺时针旋转为负。0度表示反向模拟所设计的模具。
从表中可以看出当角度位于-5~0度之间时,基本满足横向流动最小化原则,这说明所设计的模具是较优的。
3.4 实验验证
根据反向模拟设计的口模加工了模具,在上海宝山迦南塑料厂进行了挤出实验,采用 单螺杆挤出机,牵引速率为22mm/s,挤出温度修正为210℃。口模平直段长度为10mm,口模和定型模之间的距离约为50mm,与模拟的设置近似,采用真空水冷定型,定型模长度为140mm。挤出产品如图8所示,产品上表面的几何尺寸和光洁度达到了设计要求,这说明反向设计的模头达到了生产实际的要求。

图8 内侧灯罩产品
五、结论
本文使用Ployflow软件对内侧灯罩的挤出过程进行了数值模拟,利用其反向挤出功能设计出了较好的挤出模头,并进行了模具加工,在挤出机上进行了挤出实验,实验结果显示试模次数大大减少,模具使用稳定性得到了明显提高,这对类似的复杂截面塑料异型材模具的设计同样具有着重要的借鉴价值。
参考文献
[1] Srinivasa R. Vaddiraju, M. Kostic, L. Reifschneider, et al, Extrusion Simulation and Experimental Validation to Optimize Precision Die Design[C], ANTEC 2004 conference proceedings, Chicago, SPE ANTEC, 2004,1:76-80. [2] 刘斌,马骏. Polyflow逆向挤出功能在异型材口模设计中的应用[J].塑料科技,2008,36(1):66-70 [3] 戴元坎,郭营,俞炜,周持兴. 三元乙丙橡胶在简单口型中的正向挤出分析及逆向口型设计[J].合成橡胶工业,2007,30(02):124-128. [4] Y.K.Dai, C.X.Zhou, W.Yu. Inverse designing simulation of extrusion die of auto rubber seal and verifications[J]. Plastics, Rubber and Composites,2007, 36(4):141-148. [5] B.L.Koziey, J.Vlachopoulos, J.Vlek, Jsvabik. Profile die design by pressure balancing and cross flow minimization[C]. ANTEC 1996 conference proceedings, Indianapolis, SPE ANTEC, 1996, 1:247-252. [6] 朱元吉,胡善刚,郁军. 关于提高塑料异型材挤出模稳定性的调研[J].化学建材,2003,(01):17-19.
[7] 张振,朱元吉. 基于Polyflow的塑料异型材挤出模头功能块流道的设计[J]. 模具工业,2007,33(7):61-64.





