整车NVH开发关键技术,掌握车身连接点动刚度分析及优化
刚度是指结构或材料抵抗变形的能力。由于结构或材料所受荷载的不同,可能受到静载荷或动载荷,因此,刚度又分为静刚度和动刚度。当结构或材料受到静载荷时,抵抗静载荷下的变形能力称为静刚度;当受到动载荷时,抵抗动载荷下的变形能力称为动刚度。结构或材料既有静刚度又有动刚度。
一、基础知识
若某一单自由度阻尼振动系统可表示如下。

图1 单自由度阻尼系统示意图
其系统时域动力学运动方程为:
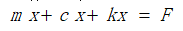
假设其方程的解是简谐运动如下,其中x0为复常数:

通过代表计算可得到系统的频域方程为:

即动刚度可表述为:

其动刚度的幅值可表述为:

由上式可知:
动刚度是一个与频率相关的复数; 动刚度与系统的质量、静刚度以及阻尼有关; 当频率为0时,即w=0,此时动刚度等于静刚度。

图2 动刚度与频率关系曲线
从上图中可以看出:
(1)在低频段,动刚度接近静刚度k,即在低频区域占主导地位的是刚度。如果作用在系统的外力变化很慢,即外力变化的频率远小于结构的固有频率时,可以认为动刚度和静刚度基本相同;
(2)在高频段,动刚度的幅值为ω2m,表明共振频率以上的频率段主要用占主导地位的质量项来描述,这是因为质量在高频振动中,产生很大的惯性阻力。当外力的频率远大于结构的固有频率时,结构则不容易变形,即变形较小,此时结构的动刚度相对较大,也就是抵抗变形的能力强;
(3)在共振频率处动刚度的幅值下降明显,其幅值为ωc,表明在共振频率处主要受阻尼控制。而在共振频率处,结构很容易被外界激励起来,此时采用一些阻尼方案可进行共振峰值的抑制。
二、动刚度的分析基础
动刚度分析方法一般采用模态频率响应方法,对车身某一点进行激励,得到同一点的响应,即为原点动刚度。通过运动方程可得到动刚度为:
Kd=F/X,动刚度是与激励频率有关的函数,随着频率 ω 的变化而改变,包含实部和虚部。

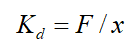
IPI(Input Point Inertance)为加速度与力的比值,即为加速度导纳,在实际工程中人们为了更好交流,一般将IPI表述为动刚度:

三、动刚度的分析流程
1、动刚度求解设置(部分摘录)
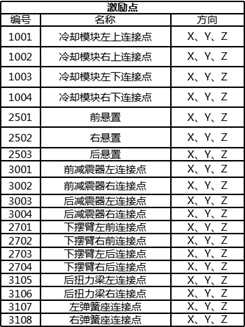
如需要对某一车型的底盘连接点进行动刚度分析,其主要求解参数如下:
冷却模块连接点处分别施加X,Y,Z方向的激励,大小1N; 动力总成连接点处分别施加X,Y,Z方向的激励,大小1N; 减震器连接点处分别施加X,Y,Z三向的激励,大小1N; 摆臂连接点处分别施加X,Y,Z三向的激励,大小1N; 后扭力梁连接点处分别施加X,Y,Z三向的激励,大小1N; 后悬弹簧连接点处分别施加X,Y,Z三向的激励,大小1N;



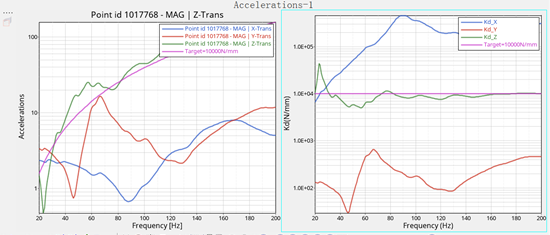
2、动刚度计算结果
根据动刚度理论,若采用的是加速度响应(亦可采用位移、速度),通过求解可得到所求连接点的动刚度曲线。一般将曲线处理成以下形式,横坐标为频率,纵坐标为加速度(由于是施加单位力,此时的纵坐标单位为mm/s^2/N),这种曲线实际为加速度导纳曲线,但我们也称为动刚度曲线,并采用对数形式,以便于察看和对问题的识别。

四、动刚度的后处理方法
动刚度即刚度是随频率变化的,当激励点和响应点是同一点的时候,所得到的刚度为原点动刚度。白车身动刚度分析所考察的是在所关注的频率范围内该接附点的刚度水平,刚度过低必然引起更大的噪声。动刚度结果采用不同的处理方法,其结果有所差异。常用的处理方法一般有平均动刚度法、指数法、面积法以及三分之一倍频程法等。
1、平均法,平均法动刚度结果相对较为粗糙,且结果一般偏大,可根据公式直接对曲线进行处理,亦可通过文本进行快速处理等;

2、指数法,根据IPI计算公式可得到Kd公式如下,通过计算每个频率点对应的刚度值,再进行所有频率叠加计算,可通过文本或表格进行快速处理;

3、面积法,其中面积法是通过IPI曲线所包围的面积计算得到,其公式推导如下,源点加速度导纳公式为

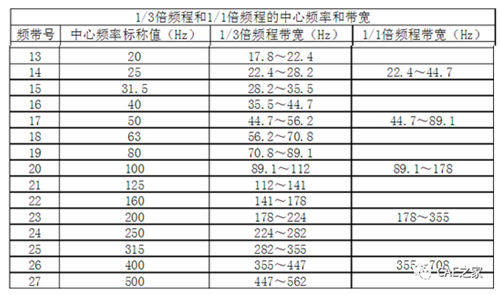
4、三分之一倍频程方法,主要是通过中心频率进行计算,可去除局部峰值的影响,如一般动刚度考虑50-200Hz,200-500Hz或20-200Hz,200-500Hz等等,下图为三分之一倍频程中心频率与带宽关系。

5、通过采用不同方法动刚度结果有所差异,其结果列表如下(20-200Hz范围内)。在实际工程中,在性能目标定义时应该统一同一种方法即可,包括分析及后面的实车测试,这样的分析优化等才具有一定的指导意义。

五、动刚度优化方法及实际应用
由于车身连接点动刚度主要与局部性能有关,包括局部刚度及模态等,可通过找出薄弱区域,再优化断面结构、连接形式以及加强件等等方法达到性能要求;如某车悬置布置中,动力总成右悬置与轮罩搭接,其侧向动刚度提升效果明显。

(完)
作者:CAE之家,仿真秀专栏作者





