基于Ansys转子动力学有限元计算方法(附直播教程)
一、写在前面
转子动力学的研究,最早可追溯到十九世纪六十年代。一个多世纪以来,随着大工业的发展,转子系统被广泛地应用于包括燃气轮机、航空发动机、工业压缩机等机械装置中,在电力、航空、机械、化工、纺织等领域中起着非常重要的作用。因而,转子动力学有着极强的工程应用背景,其相关的研究工作也越来越受到人们的重视。
本文先通过Ansys研究了某电机转子的动力学问题,为转子动力学设计找到了一个新的途径。然后学习转子动力学计算中几个专业术语,最后带给朋友们一个基于Ansys转子动力学有限元计算方法直播教程。
二、基于ANSYS电机转子的动力学分析
1、模型的建立及计算
如图1所示,为电子转子的有限元模型,使用BEAM188单元模拟转子的轴,使用MASS21单元模拟转子,使用单元COMBI214模拟轴承。
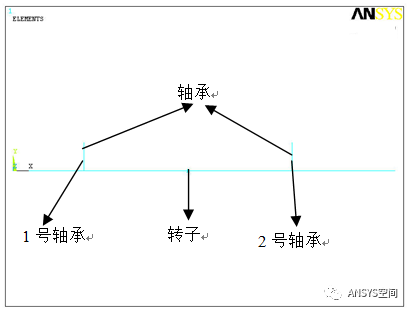
图1 电机转子的有限元模型(不显示单元)
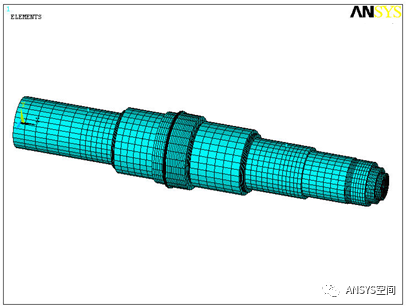
图2 电机转子的有限元模型(显示单元)
图3给出了Beam188 单元的几何简图。Beam188单元适合于分析从细长到中等粗短的梁结构,该单元基于铁木辛哥梁结构理论,并考虑了剪切变形的影响。
Beam188 是三维线性(2 节点)或者二次梁单元。每个节点有六个或者七个自由度,自由度的个数取决于KEYOPT(1)的值。
当KEYOPT(1)=0(缺省)时,每个节点有六个自由度;节点坐标系的x、y、z 方向的平动和绕x、y、z 轴的转动。
当KEYOPT(1)=1 时,每个节点有七个自由度,这时引入了第七个自由度(横截面的翘曲)。这个单元非常适合线性、大角度转动和/并非线性大应变问题。当NLGEOM 打开的时候,beam188 的应力刚化,在任何分析中都是缺省项。应力强化选项使本单元能分析弯曲、横向及扭转稳定问题(用弧长法)分析特征值屈曲和塌陷)。
Beam188可以采用sectype、secdata、secoffset、secwrite 及secread定义横截面。本单元支持弹性、蠕变及素性模型(不考虑横截面子模型)。这种单元类型的截面可以是不同材料组成的组和截面。 图4给出了COMBI214单元的几何简图。
COMBI214是专门用来模拟轴承力学性质的单元,可以考虑拉压,但不能考虑弯曲和扭转。这个弹簧阻尼单元没有质量,如果需要质量则通过添加MASS21单元来实现。


图4 COMBI214单元的几何模型简图
表1到表3分别给出了转轴的计算参数和两个轴承的计算参数。转子外载荷为重力和扭矩。进行谐响应分析来找出电机转子的共振频率点。以便使转子的实际工作转速避开此点。不考虑转子加工的所引起的质量偏心,而只考虑转轴因受到重力而产生的偏心。电机的驱动力矩的频率从0变化到400Hz间隔为0.5Hz。



图5 电机转子的考察点

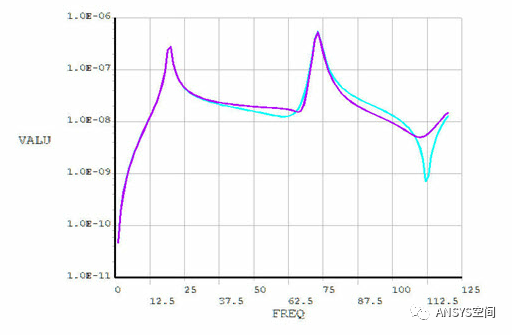
图6 各考察点的位移与频率的关系

图7 162Hz时的转子的位移云图

图8 162Hz时的转子的等效应力云图

图9 240Hz时的转子的位移云图

图10 240Hz时的转子的位移云图
图6到图10给出了电机转子的计算结果:图6给出了5个考察点的y方向的位移与激励频率的关系图,由图可知:电机转子有两个共振点分别是162Hz和240Hz,且电机右端点处的振动幅度最大,电机转子左端点和中心转子处的振动幅度相当。
图7和图8给出一阶共振频率的位移等效云图和应力等效云图,由两图可知当外界的激励频率达到160Hz时,电机作摆振,且最大应力为7.8MPa。
图9和图10给出了二阶共振频率时的电机位移和等效应力云图。由图可知:电机的二阶共振频率的位移和应力远小于一阶的值,因此对于本文的电机轴主要要避开一阶共振点。
通过以上分析和计算可以得出以下结论:
第一、以上提出的使用BEAM188单元模拟转子的轴,使用MASS21单元模拟转子,使用单元COMBI214模拟轴承,对于研究转子动力学操作简单,计算可靠,为转子动力学的数值计算提供了一个可行的方法。
第二、通过计算本文的电机转子存在两个主要的共振点,分别是162Hz和240Hz。
1、陀螺效应
所谓陀螺效应,就是旋转着的物体具有像陀螺一样的效应。陀螺有两个特点:进动性和定轴性。简单来说,陀螺效应就是旋转的物体有保持其旋转方向(旋转轴的方向)的惯性。
对于一个绕轴Δ旋转的结构,如果在垂直于轴Δ施加一个扰动会发生进动且会出现反力矩。这个反力矩就是陀螺力矩。陀螺力矩的轴即垂直于旋转轴也垂直于进动轴。这将导致陀螺矩阵耦合了垂直于旋转轴平面上的自由度。这也导致陀螺矩阵为非对称矩阵。
2、涡动
转子正常的旋转也包含了涡动的概念。例如转子在不平衡力矩作用下,转轴发生挠曲变形,转轴以角速度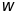 在空间旋转,此时转轴的运动实际上是两种运动的合成。
在空间旋转,此时转轴的运动实际上是两种运动的合成。
一种是转轴绕其轴线的定轴转动,转动角速度就是旋转速度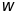 ;另一种则是变形的轴线绕其静平衡位置的空间回转,回转角速度仍然是
;另一种则是变形的轴线绕其静平衡位置的空间回转,回转角速度仍然是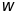 。后种回转运动就是涡动。这就像小孩玩跳绳一样,转轴第一种转动犹如跳绳本身旋转,转轴第二种转动犹如弓状的跳绳在空间回转,因此称它为弓状回转,在这里称为涡动。
。后种回转运动就是涡动。这就像小孩玩跳绳一样,转轴第一种转动犹如跳绳本身旋转,转轴第二种转动犹如弓状的跳绳在空间回转,因此称它为弓状回转,在这里称为涡动。
正常转轴的涡动角速度Ω和旋转角速度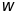 相等,因此称它为同步涡动。凡是同步涡动,如转轴上某一方向受拉或受压,则在旋转状态下将始终受拉或受压。但是当转子发生自激振动时,由于涡动转速与转子转速不符,将发生异步涡动。如果涡动的运动方向与旋转方向相同称为正向涡动(FW),反之则为反向涡动(BW)。
相等,因此称它为同步涡动。凡是同步涡动,如转轴上某一方向受拉或受压,则在旋转状态下将始终受拉或受压。但是当转子发生自激振动时,由于涡动转速与转子转速不符,将发生异步涡动。如果涡动的运动方向与旋转方向相同称为正向涡动(FW),反之则为反向涡动(BW)。
不论是正向涡动还是反向涡动,转轴上某一方向将交替受拉或受压,即转子在转动状态下转子上高点位置周期性顺转向或逆转向移动。显然,当涡动速度低于转子转速时,转子上高位置将逆转向移动,反之则顺转向移动,移动速度为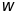 -Ω或Ω-
-Ω或Ω-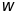 。
。
3、椭圆轨迹
在大多数情况下,旋转轴上的节点稳态轨道也叫做轨迹且是个椭圆形状。它的特点如下:在局部坐标系XYZ中,x轴为旋转轴,在节点I处的椭圆由长半轴A,短半轴B和相位角ψ (PSI),定义如图所示。
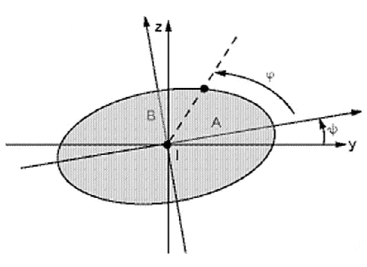
图11 转子的椭圆轨迹图
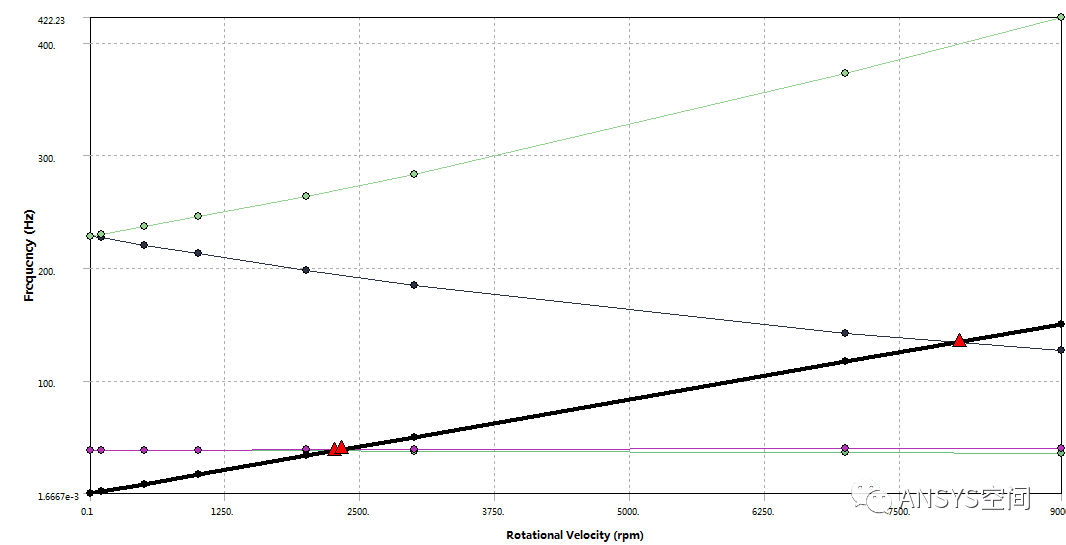
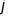 (PHI)定义了节点的初始位置。为了比较结构中两个节点的相位,用户要检查
(PHI)定义了节点的初始位置。为了比较结构中两个节点的相位,用户要检查 ψ φ。YMAX和ZMAX分别是沿着Y轴和Z轴方向上的最大位移。
ψ φ。YMAX和ZMAX分别是沿着Y轴和Z轴方向上的最大位移。
4、稳定性
转子保持无横向振动的正常运转状态的性能。若转子在运动状态下受微扰后能恢复原态,则这一运转状态是稳定的;否则是不稳定的。转子的不稳定通常是指不存在或不考虑周期性干扰下,转子受到微扰后产生强烈横向振动的情况。转子稳定性问题的主要研究对象是油膜轴承。油膜对轴颈的作用力是导致轴颈乃至转子失稳的因素。该作用力可用流体力学的公式求出,也可通过实验得出。
一般是通过线性化方法,将作用力表示为轴颈径向位移和径向速度的线性函数,从而求出转子开始进入不稳定状态的转速——门限转速。导致失稳的还有材料的内摩擦和干摩擦,转子的弯曲刚度或质量分布在二正交方向不同,转子与内部流体或与外界流体的相互作用,等等。有些失稳现象的机理尚不清楚。
旋转结构自励的振动在一段时间内会引起振幅的增加如图12所示:
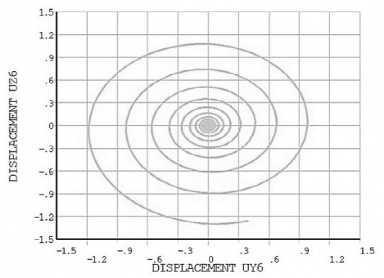
图12 转子中心轨迹图
如果没有检查,旋转结构出现了不稳定状态则能够导致设备的损坏
旋转结构的不稳定的常见原因:
-轴承特性;
-内部的旋转阻尼 (材料阻尼);
-旋转部分和静态部件之间的接触。
此外,基于ANSYS软件还可以解决以下转子动力学问题:
(1)临界转速计算
(2)临界转速映射图

(3)转子轨迹
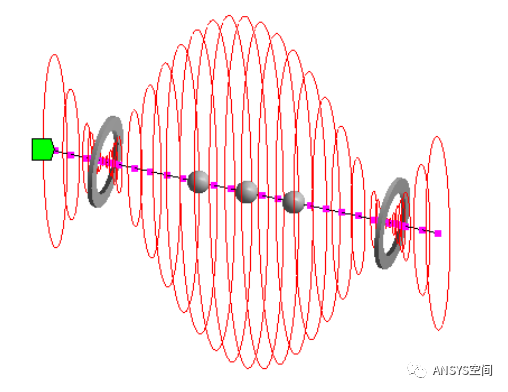
(4)不平衡响应激励
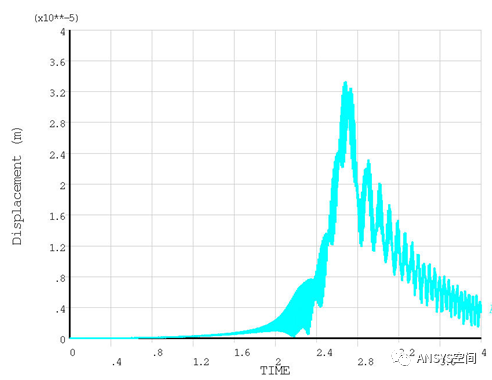
(5)转子启动的瞬态响应
(6)动压轴承的参数计算

作者:张老师,仿真秀年度优秀讲师




