仿真好内容提名《Workbench热力学分析实例演练（2020版）》

2年前浏览3402

作者 | 刘成柱等著机械工业出版社

首发 | 仿真秀App

一、导读

自《一场褒奖仿真好内容的盛典》活动公开发布以来！我们不仅受到了大量仿真类公众号提名，我们还特别收到了机械工业出版社、中国水利水电出版社、清华大学出版社、电子工业出版社、人民邮电出版社、化学工业出版社和个人提名了多本仿真类书籍。今天我们重点推荐由机械工业出版社提名的仿真好书《ANSYS Workbench热力学分析实例演练（2020版）》。欢迎大家后续为其投票，以下是正文：

二、写在文前

在自然界和工程中，很多导热过程是非稳态的，即温度场是随时间而变化的。例如，室外空气温度和太阳辐射的周期变化引起房屋维护结构（墙壁、屋顶等）温度场随时间变化；采暖设备间歇供暖时引起墙内外温度随时间变化，这些都是非稳态导热过程。

按照过程进行的特点，非稳态导热过程可以分为周期性非稳态导热过程和瞬态非稳态导热过程两大类。在周期性非稳态导热过程中，物体的温度按照一定的周期发生变化。例如，以24h为周期，或以8760h（即一年）为周期。温度的周期性变化使物体传递的热流密度也表现出周期性变化的特点。

在瞬态导热过程中，物体的温度随时间不断地升高（加热过程）或降低（冷却过程），在经历相当长的时间之后，物体的温度逐渐趋近于周围介质的温度，最终达到热平衡。本章将分别对两类非稳态导热过程进行分析和阐述。

1、非稳态导热的基本概念

首先分析瞬态导热过程。以采暖房屋外墙为例来分析墙内温度场的变化。假定采暖设备开始供热前，墙内温度场是稳态的，温度分布的情形如图6-1a所示，室内空气温度为，墙内表面温度为，墙外表面温度为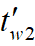，室外空气温度为。

当采暖设备开始供热时，室内空气很快上升到并保持稳定。由于室内空气温度的升高，它和墙内表面之间的对流换热热流密度增大，墙壁温度也随之升高如图6-1b所示。

开始时升高的幅度较大，依次地和升高的幅度较小，而在短时间内几乎不发生变化。随着时间的推移，各层温度将逐渐地按不同幅度升高。是室外空气温度，假定在此过程中保持不变。

关于热流密度的变化，一开始由于墙内表面温度不断地升高，室内空气与它之间的对流换热系数密度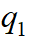会不断减小；而墙外表面与室外空气之间的对流换热密度却因墙外表面温度随时间不断升高而逐渐增大，如图6-1c所示。与此同时，通过墙内各层的热流密度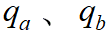和也将随时间发生变化，并且彼此各不相等。

在经历一段相当长时间之后，墙内温度分布趋于稳定，建立起新的稳态温度分布，即图6-1a中的。当室内尚未开始供热之前，墙内和室内外空气温度是稳态的，所以等于，而且等于通过墙的传热量。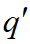

在两个稳态之间的变化过程中，热流密度和是不相等的，它们的差值（即图6-1c中的阴影面积）为墙本身温度的升高提供了热量。所以，瞬态导热过程必定伴随着物体的加热或冷却过程。

图6-1 瞬态导热的基本概念

综上所述，在物体的加热或冷却过程中，温度分布的变化可以划分为三个基本阶段。第一阶段是过程开始的一段时间，它的特点是温度变化从边界面（如上述案例中墙内表面），逐渐深入物体内部，此时物体各处温度随时间的变化率是不一样的，温度分布受初始温度分布的影响很大，这一阶段称为不规则情况阶段。

随着时间的推移，初始温度分布的影响逐渐消失，进入第二阶段，此时物体内各处温度随时间的变化率具有一定的规律，称为正常情况阶段。物体加热和冷却的第三阶段就是建立新的稳态阶段，在理论上需要经过无限长的时间才能达到，事实上经过一段较长的时间后，物体各处的温度就可近似地认为已达到新的稳态。

周期性的非稳态导热也是供热和空调工程中常遇到的一种情况。例如，夏季室外空气温度以一天24h为周期进行周而复始的变化，相应地室外墙面温度也以24h为周期进行变化，但是它比室外空气温度变化滞后一个相位，如图6-2a所示。

图6-2 周期性导热的基本概念

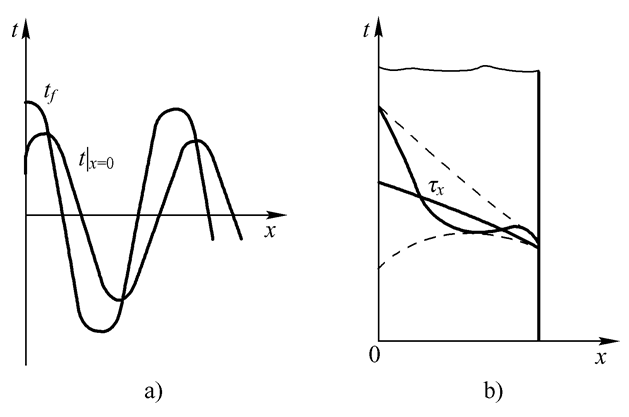
这时尽管空调房间室内温度维持稳定，但墙内各处的温度受室外温度周期变化的影响，也会以同样的周期进行变化，如图6-2b所示，图中两条虚线分别表示墙内各处温度变化的最高值与最低值，图中的斜线表示墙内各处温度周期性波动的平均值。如果将某一时刻墙内各处的温度连接起来，就得到时刻墙内的温度分布。

上述分析表明，在周期性非稳态导热问题中，一方面物体内各处的温度按一定的振幅随时间进行周期性波动；另一方面，同一时刻物体内的温度分布也呈周期性波动，如图6-2b所示的时刻墙内的温度分布。这就是周期性非稳态导热现象的特点。

在建筑环境与设备工程专业的热工计算中，这两类非稳态导热问题都会遇到，而热工计算的目的，归根到底就是要找出温度分布和热流密度随时间和空间的变化规律。

2、无限大平壁导热分析

接下来介绍了一个二维的无限大平壁的导热过程的解析计算方法与仿真操作流程。

（1）问题描述

本实例为一个无限大平壁，厚度为0.5m，已知平壁的热物性参数

壁内温度初始时均匀一致为18℃，给定第三类边界条件：壁两侧面流体温度为8℃，流体与壁面之间的表面传热系数，试求6h后平壁中心及表面的温度。

（2）解析方法计算

【解】根据平壁的热物性参数求平壁的热扩散率：

确定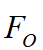和准则：

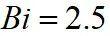因为，可以用公式（6-31）计算。此时可知当时，。于是

应用式（6-31），对于平壁中心，即x=0 处，无量纲温度为

而

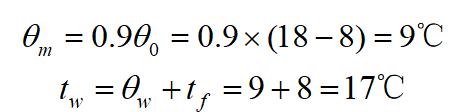
对于平壁表面，即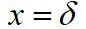处，无量纲温度为

而

（3）创建分析项目

Step1：在Windows系统下启动ANSYS Workbench，进入主界面。
Step2：在Workbench平台中依次选择菜单Tools→Options，如图6-3所示。
Step3：在弹出的Options（设置）对话框中选择Geometry Import选项，在Analysis Type栏选择分析类型为2D，其余默认即可，如图6-4所示，单击OK按钮。

图6-3 菜单

图6-4 分析类型

Step4：双击主界面Toolbox（工具箱）中的Analysis Systems→Steady-State Thermal（稳态热分析）选项，即可在Project Schematic（项目管理区）创建分析项目A，然后以同样的操作方式拖曳一个Transient Thermal（瞬态分析）到A6（Solution）中，如图6-5所示。

图6-5 创建分析项目A

（4）创建几何体模型

Step1：在A3：Geometry上单击右键，在弹出的快捷菜单中选择New DesignModeler Geometry命令，如图6-6所示。

图6-6 导入几何体

Step2：在启动的DM几何建模窗口中进行几何创建。设置长度单位为mm，单击DM窗口中的Tree Outline→XYPlane，再选择Sketching选项卡，选择Draw→Rectangle命令，从坐标原点开始绘制一个矩形。
Step3：选择Dimensions→General，标注矩形的长和宽，如图6-7所示，设置V1=2000mm，H2=500mm。

图6-7 标注

Step4：切换到Modeling选项卡，依次选择Concept→Surface From Sketches（从草绘生成面）命令，如图6-8所示。
Step5：在Details View详细设置面板中的Base Objects栏选择刚才建立的Sketch1，并单击工具栏中的“生成”命令，如图6-9所示。

图6-8 菜单

图6-9 模型

Step6：几何生成完成后，单击工具栏中的按钮，在弹出的“另存为”对话框的名称栏输入ex5.wbpj，并单击“保存”按钮。
Step7：回到Designmodeler界面中，单击右上角的（关闭）按钮，退出Designmodeler，返回到Workbench主界面。

（5）创建分析项目

Step1：在Workbench主界面右击A2：Engineering Data项，在弹出的图6-10所示的快捷菜单中选择Edit命令。

图6-10 快捷菜单

Step2：在Outline of Schematic A2，B2：Engineering Data栏中的Material中输入材料的名称为mat，然后从左侧的Toolbox栏中的Thermal下选择Isotropic Thermal Conductivity（各向同性导热系数）并直接拖曳到mat中，此时在Properties of Outline Row 4：mat下面的Isotropic Thermal Conductivity中输入0.815，同样Density为1500，Specific Heat为839，输入完成后，在工具栏中单击中的“关闭”按钮关闭材料设置窗口，如图6-11所示。

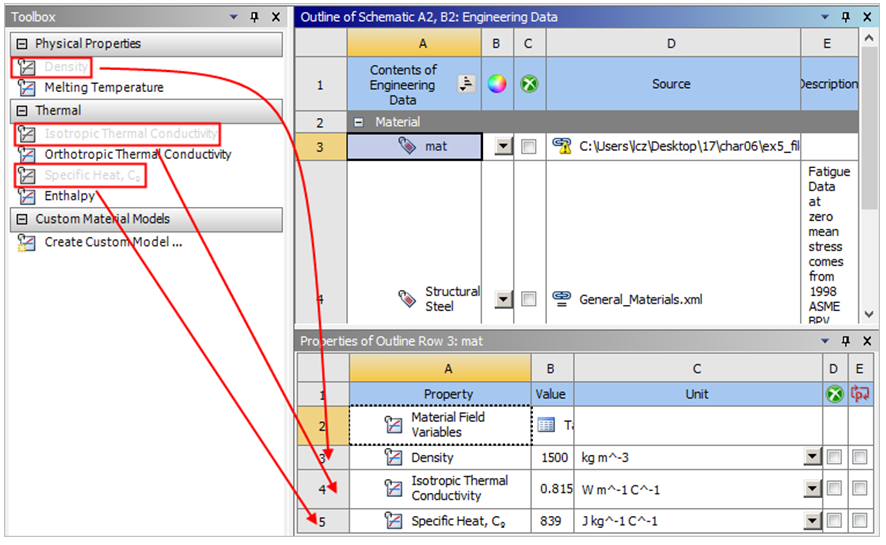
图6-11 设置材料

Step3：双击主界面项目管理区项目A中的A4：Model项，进入图6-12所示的Mechanical界面，在该界面下可进行网格的划分、分析设置、结果观察等操作。
Step4：选择Mechanical界面左侧Outlines（分析树）中Geometry选项下的Surface Body，此时即可在Details of“Surface Body”（参数列表）中给模型添加材料，如图6-13所示。
Step5：单击参数列表中的Material下Assignment黄**域后的，此时会出现刚刚设置的材料mat，选择即可将其添加到模型中去。

图6-12 Mechanical界面

图6-13 修改材料属性

（6）划分网格

Step1：右击Mechanical界面左侧Outline（分析树）中的Mesh选项，在弹出的快捷菜单中依次选择Insert→Sizing命令，如图6-14所示。

图6-14 快捷菜单

Step2：在Details of“Edge Sizing”详细设置面板中作如下操作：在Geometry栏中选中图示上的四条边，并单击Apply按钮，如图6-15所示；在Element Size栏输入5.e-002m，其余默认即可。
Step3：在Outlines（分析树）中的Mesh选项单击鼠标右键，在弹出的快捷菜单中选择 Generate Mesh命令，最终的网格效果如图6-16所示。

图6-15 网格设置

图6-16 网格效果

（7）施加载荷与约束

Step1：选择Mechanical界面左侧Outline（分析树）中的Steady-State Thermal（A5）选项，如图6-17所示，此时会出现Environment工具栏。
Step2：选择Environment工具栏中的Temperature（温度）命令，此时在分析树中会出现Temperature选项，如图6-18所示。

图6-17 Environment工具栏

图6-18 添加载荷

Step3：如图6-19所示，选中Temperature，在Details of“Temperature”中作如下操作：

图6-19 施加载荷

在Geometry中选择选择几何表面；在Definition→Magnitude栏输入18℃（ramped）；其余默认即可，完成一个温度的添加。
Step4：在Outlines（分析树）中，选择Steady-State Thermal（A5）选项并单击鼠标右键，在弹出的快捷菜单中选择Solve命令，如图6-20所示。

图6-20 求解

（8）瞬态计算

Step1：选择Mechanical界面左侧Outline（分析树）中的Transient Thermal (B5)（瞬态计算）选项，此时会出现图6-21所示的Environment工具栏。
Step2：选择Environment工具栏中的Convection（对流）命令，此时在分析树中会出现Convection选项，如图6-22所示。

6-21 Solution工具栏

图6-22 添加对流选项

Step3：选择Convection命令，在出现的Details of “Convection”详细设置面板中进行如下设置，如图6-23所示：在Geometry栏中选中两侧的边线；在Film Coefficient栏输入对流系数为8.15；在Ambient Temperature栏输入环境温度为8℃，其余默认即可。
Step4：设置分析选项。单击Transient Thermal（B5）下面的Analysis Settings（分析设置），在图6-24所示的分析选项设置窗口中进行如下设置：在Step End Time栏输入21600s；在Auto Time Stepping栏选择off；在Define By栏选择Substeps；在Number Of Substeps栏输入100，其余默认即可。

图6-23 对流选项

图6-24 分析设置

Step5：在Outlines（分析树）中选择Solution（B6）选项并单击鼠标右键，在弹出的快捷菜单中选择 Solve命令，如图6-25所示，此时会弹出进度显示条，表示正在求解，当求解完成后进度条自动消失。
Step6：选择Outline（分析树）中Solution（B6）下的Total Deformation（总变形），得出温度分布图如图6-26所示。
Step7：单击Solution→Solution Information→Temperature-Global Maximum，将显示图6-27所示的温度曲线图。