浅析橡胶超弹体与粘弹性仿真计算方法(粘弹性篇)
- 作者优秀
- 优秀教师/意见领袖/博士学历/特邀专家/独家讲师
- 平台推荐
- 内容稀缺
本文摘要(由AI生成):
本文介绍了橡胶粘弹性仿真计算方法,包括基于Prony级数模型的剪切模量表示、时间和温度的拟时间概念,以及William-Landel-Ferry (WLF)偏移函数方程在温度改变下的应用。文章还详细解释了WLF方程中参数的确定方法,并展示了橡胶粘弹性仿真计算的控制要素和案例应用。案例涉及罐体法兰密封结构的计算,通过超弹体和粘弹性材料本构拟合曲线试验数据,进行螺栓预紧力下密封圈密封压力数值的获取和应力松弛状态的判断。文章旨在帮助初学者理解橡胶粘弹性仿真计算方法,并对企业生产、研发提供一定的帮助。
一、写在文前
有些非晶态聚合物的行为随温度而改变,在玻璃态转变温度以下,材料行为与弹性固体类似;在玻璃态转变温度以上,材料响应与“橡胶”固体类似;在高温下,材料行为与粘性液体类似。在玻璃态转变温度以上,“橡胶”固体响应是弹性固体和粘性液体的行为结合,这种行为具有粘弹性的特性。粘弹性材料特性与时间-温度有关,响应可以看做是弹性和粘性部分的组成,弹性部分瞬时可以恢复,而粘性部分不可恢复且伴随全部时间发生。二、橡胶粘弹性材料曲线拟合
橡胶粘弹性仿真计算首要进行橡胶粘弹性试验获得的材料数据曲线拟合工作,主流工程仿真软件都能有效完成,以ANSYS Workbench软件平台提供的材料数据“Engineering Data”模块为例,进行定义粘弹性材料属性的说明,如图1所示。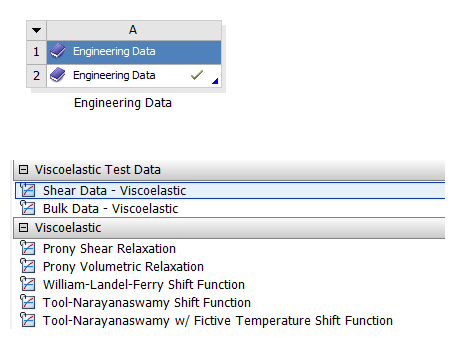
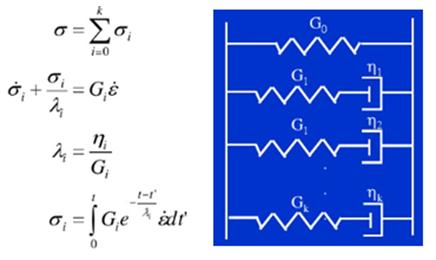
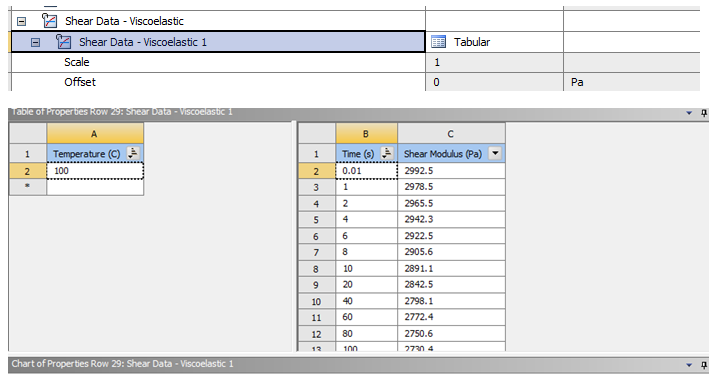
粘弹性测试数据支持剪切或者体积测试数据,以剪切数据为例进行说明,双击添加“ShearData-Viscoelastic”项目,同时添加对应“Prony Shear Relaxation”项目。ANSYS采用应力松弛函数的Prony级数表示法模拟粘弹性,如图2所示,流变模型依赖于两个基本模型,其中弹簧模型定义应力和应变关系代表弹性固体,缓冲器模型定义应力和应变率之间行为代表粘性流体,ANSYS采用广义Maxwell模型,K个并联弹簧和缓冲器,如图3所示。“ShearData-Viscoelastic”项目表中填写相关试验温度与对应剪切模量和松弛时间对应数据,如图4所示。对试验数据曲线拟合定义拟合项数,对于项数跳出列表松弛时间种子值赋值应该与试验数据松弛时间匹配,保证“Curve Fitting”曲线拟合与试验数据点吻合,否则如图所示5拟合图的默认种子值不匹配将会导致拟合度较差。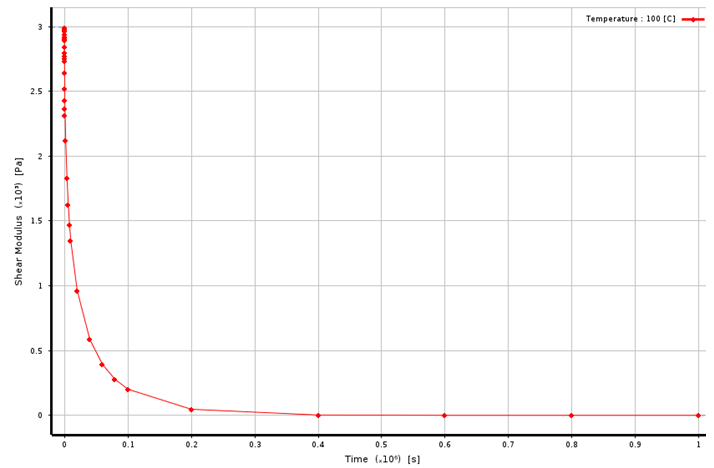
图4
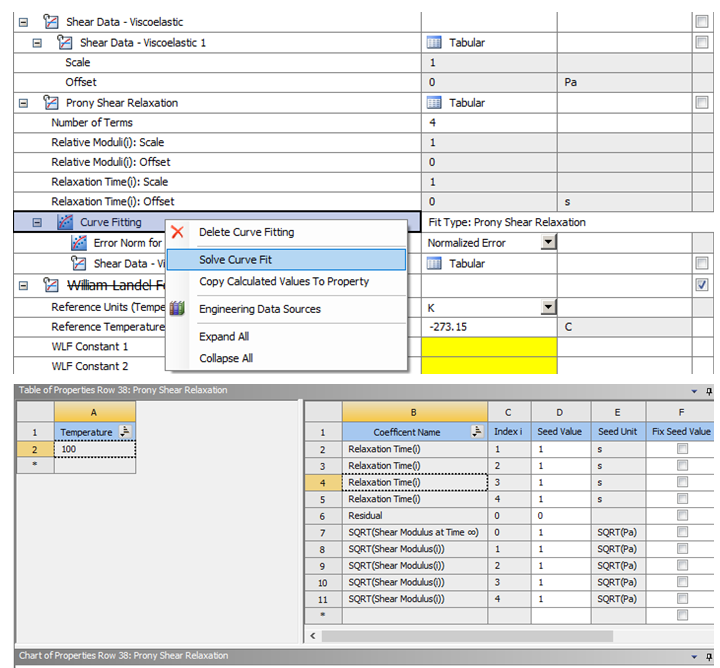

右键选择“Solve Curve Fit”进行曲线拟合后,再次右键“Copy Calculated values to property”自动录入数据进入“Prony ShearRelaxation”项目。三、时温等效与简单热流变
简单热流变行为该假设考虑了时间与温度相关的关系,意味着时间和温度具有同一现象,该假设的结果是短项G(t=0)和长项G(t=∞)模量保持一致,与温度无关(即对于任何平移,曲线图的上下限保持一致)。响应与对数时间的函数关系随温度变化而平移足以表述多种非晶态聚合物粘弹性,这样可以在某一温度下定义粘弹性行为而捕捉其他温度下的响应。利用缩减时间和偏移函数的概念,粘弹性响应曲线被“移动”来说明另一个温度下的行为,根据材料的不同采用相应的偏移函数,ANSYS支持两个不同偏移函数和一个用户自定义偏移函数,其中William-Landel-Ferry (WLF)偏移函数主要应用于橡胶类产品。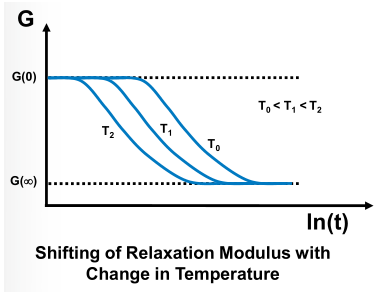
另一种解释是时温等效原理认为同一个力学松弛现象(应力松弛指在恒定的外加应变作用下,应力逐渐降低),既可以在较高温度下短时间观测,也可以在较低温度下长时间内观测,即升高温度和延长观测时间对于聚合物粘弹性行为是等效的。
四、William-Landel-Ferry (WLF)偏移函数
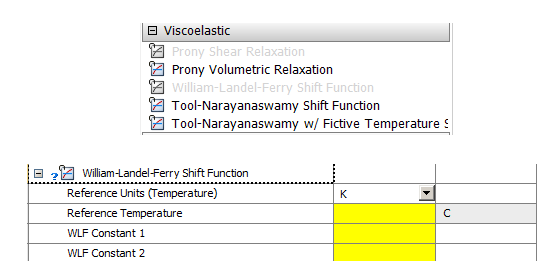
ANSYS利用William-Landel-Ferry (WLF)偏移函数模拟橡胶类聚合体粘弹性单元该行为。William-Landel-Ferry (WLF)是高分子物理中重要的经验公式,如下。一般C1和C2材料属性由试验中不同温度下松弛时间来确定,使用WLF偏移函数时,在给定温度Tr下定义剪切/体积模量的松弛参数,基于不同温度下的试验松弛数据,能够推导C1和C2,于是偏移函数把Tr的松弛曲线和温度的变化进行联系。William-Landel-Ferry (WLF)偏移函数C1,C2是两个材料经验常数,取决于参考温度Tr的取值,且其乘积为定值(C1·C2 ≈ 900)。因此剪切模量 改写为如下方程,包括时间和温度的拟时间。温度改变 按照时间增量 线性改变,所有Prony级数的松弛时间必须遵守偏移函数,因此基于偏移函数温度变化改变松弛时间,使用拟时间ξ能够进行等温方程和非等温过程的描述,如图9所示。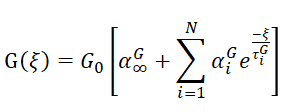
William-Landel-Ferry (WLF)偏移函数方程参数的确定,如前所述,对多数非晶态聚合物,通过把不同温度下得到的几个不同时间数量级的实验模量、温度曲线水平位移,可以叠合成一条主曲线。在时间轴上的水平位移 (注意以上提到的偏移函数 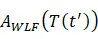 在此后都以 进行替换)符合以下关系,其中
在此后都以 进行替换)符合以下关系,其中 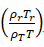 近似取1。
近似取1。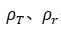 分别为温度T和参考温度T时的密度
分别为温度T和参考温度T时的密度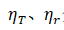 分别是温度T和参考温度T时的粘度
分别是温度T和参考温度T时的粘度
根据自由体积理论,某温度下高聚物的实际体积等于高分子本身固有体积和自由体积之和。液体粘度与本身自由体积相关,自由体积分数与温度相关,联立可得:将如下两式进行比较,获得WLF偏移方程中的C1和C2。一般认为 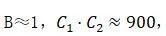 当选择玻璃化温度Tg作为参考温度时,则 具有近似的普适值(大量实验值的平均值)
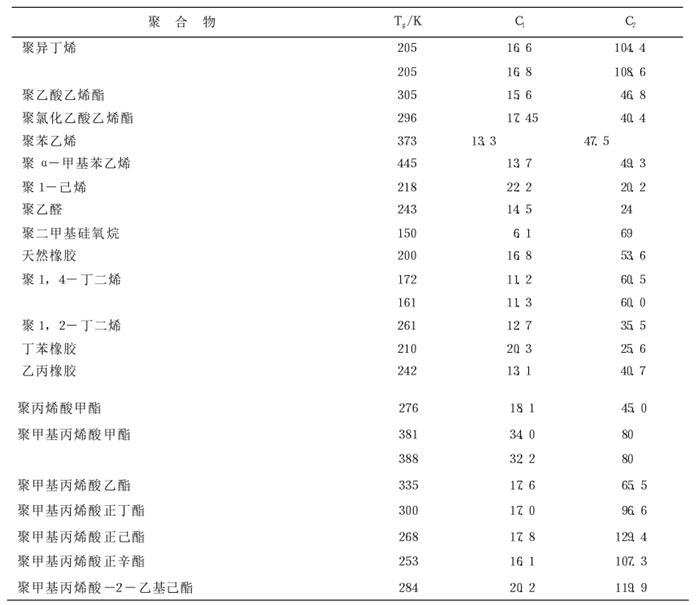
当选择玻璃化温度Tg作为参考温度时,则 具有近似的普适值(大量实验值的平均值)  WLF方程重要的意义在于低温下测定的力学数据可转换成短时间的数据或者高温时测定的力学数据可转换为长时间的数据。高分子物理教材中给出的参考值如下图所示。
WLF方程重要的意义在于低温下测定的力学数据可转换成短时间的数据或者高温时测定的力学数据可转换为长时间的数据。高分子物理教材中给出的参考值如下图所示。五、橡胶粘弹性仿真计算控制
橡胶粘弹性仿真计算前提在橡胶超弹体材料本构计算基础上添加“Prony Shear Relaxation”本构和偏移函数William-Landel-Ferry (WLF),同时需要考虑橡胶粘弹性和超弹性计算特殊的非线性求解控制和单元控制,这些已经在上一篇稿件《浅析橡胶超弹体与粘弹性仿真计算方法(超弹篇)》中进行过说明,此处不再累述。六、案例应用
如图11所示为个人工作期间曾经主导完成的某大型企业的罐体法兰密封结构计算项目,矩形密封圈进行填充密封槽进行控油防泄露。螺栓预紧力施加载荷,载荷传递保证法兰平面和密封槽底面对于密封圈上下表面施加挤压。超弹体和粘弹性材料本构拟合曲线试验数据,来源于该企业组织研究院进行的多项密封橡胶供应企业材料的测试试验。① 判断螺栓不同预紧尺度下,密封圈密封压力数值的获取,以及螺栓强度失效的可能,这部分计算内容主要由橡胶超弹体材料本构计算完成。② 判断密封圈压缩后随时间变化的应力松弛状态,进一步判断密封泄露的可能原因,这部分计算内容借助橡胶粘弹性材料本构仿真计算进行。① 通过超弹体本构计算获得密封圈在不同螺栓预紧力挤压状态下应力表现,以能够较好观察接触压力的表现,同时获得螺栓预紧力施加状态下螺栓强度的数值,指导实施安装。② 通过粘弹性本构计算获得随时间衰减的应力松弛过程,以能够观察安装后密封接触压力的更真实状态,指导复查设备。七、写在文后
本文继浅析橡胶超弹体与粘弹性仿真计算方法(超弹性篇)文稿编写之后,对于橡胶粘弹性仿真计算方法内容再次进行的编写整理,仅希望对于初学橡胶超弹体和粘弹性仿真计算的相关朋友有一定帮助作用,若是间接能帮助所在企业生产、研发攻坚,那更是非常高兴。由于个人学历经验方面对于粘弹性理解都极为浅薄,错误难免,请大家辨别阅读,若是有重大仿真理解错误请联系我们进行撤稿处理,万分感谢。(完)
作者介绍:付稣昇,仿真秀专栏作者,长期以来一直从事结构产品的强度、疲劳、复合材料、高级动力学、运动学、高级非线性、尺寸优化、拓扑优化与轻量化设计等方面仿真计算工作;擅长机械结构设计和原理联合仿真计算进行产品性能升级,先后完成仿真技术解决方案和项目实施工作若干;先后编写出版书籍《ANSYS Workbench17.0数值模拟与实例精解》与《ANSYS nCode DesignLife疲劳分析基础与实例教程》。声明:原创作品,首发仿真秀App,欢迎分享,禁止私自转载,转载请联系我们。欢迎投稿,转载或投稿请联系18610516616.获赞 10104粉丝 21585文章 3546课程 219

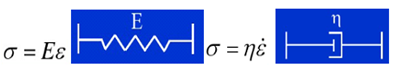






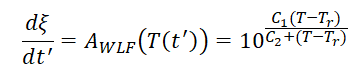
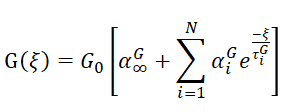

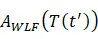 在此后都以 进行替换)符合以下关系,其中
在此后都以 进行替换)符合以下关系,其中 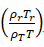 近似取1。
近似取1。
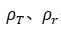 分别为温度T和参考温度T时的密度
分别为温度T和参考温度T时的密度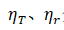 分别是温度T和参考温度T时的粘度
分别是温度T和参考温度T时的粘度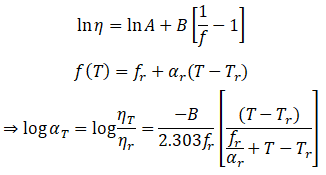


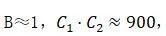 当选择玻璃化温度Tg作为参考温度时,则 具有近似的普适值(大量实验值的平均值)
当选择玻璃化温度Tg作为参考温度时,则 具有近似的普适值(大量实验值的平均值)  WLF方程重要的意义在于低温下测定的力学数据可转换成短时间的数据或者高温时测定的力学数据可转换为长时间的数据。高分子物理教材中给出的参考值如下图所示。
WLF方程重要的意义在于低温下测定的力学数据可转换成短时间的数据或者高温时测定的力学数据可转换为长时间的数据。高分子物理教材中给出的参考值如下图所示。