大型风电机组变桨变速控制器开发方法与原理

首发 | 仿真秀App

导读:几乎任何一种发电设备的设计都离不开这三个关键词:安全、稳定、高效。因为存在这些要求和目标,通常需要构造相对稳定的运行环境。火电及核电机组均可以通过锅炉输出温度和压力较为稳定的水蒸汽,推动汽轮机旋转发电;水电机组的入流水压和流量也可以人为控制。
与此不同的是,风电机组运行于风速完全不受控制的大气环境中。如何在动态变化的风况中,依然保持结构安全、运行稳定和高效发电,自然成为风电机组初始设计阶段必须克服的难题。
这就需要针对机组设计参数和运行条件,开发相应的控制系统。一个完整的大型风电机组控制系统需要实现的功能非常多,但其中必然包含变桨控制和变速控制。
今天,咱们简单聊聊大型风电机组变桨变速控制器开发吧。
一、气动载荷
本质上,变桨和变速控制都是为了改变风轮气动载荷。所以,为了理解风电机组变桨变速控制器的开发思路和方法,是无论如何也绕不开气动载荷的。
现有的风电机组载荷一体化分析软件,几乎都是采用效率极高的叶素理论计算叶片气动力。
我们常听到的叶素-动量理论是叶素理论结合动量理论后的一个方法,用于迭代求解诱导因子。
叶素理论基于有限元的思想,将一个叶片视为有限段叶素(blade element)。通过计算每个叶素上的气动力,得到整个叶片的气动载荷。
叶素理论计算效率较高的原因,就是其采用查表的方式调取翼型气动力系数(升力系数Cl和阻力系数Cd)。而传统CFD方法则需要求解翼型周围的流场,获取翼型表面压力分布,得到翼型升阻力系数,计算效率自然就低的多。
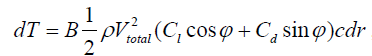
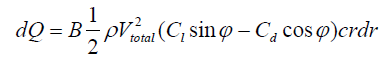
翼型升阻力系数大小除了与翼型本身的几何外形有关之外,另一个最为关键的影响因素就是:攻角(Angle of Attack,AoA),通常用希腊字母α表示。
下图为DU-21翼型在-9度~24度攻角范围内的升阻力系数,可以看出升阻力系数对攻角在较大范围内对攻角均十分敏感,特别是升力系数,在失速攻角前,与攻角基本成线性关系。所以,攻角的变化对翼型气动力的影响十分显著。
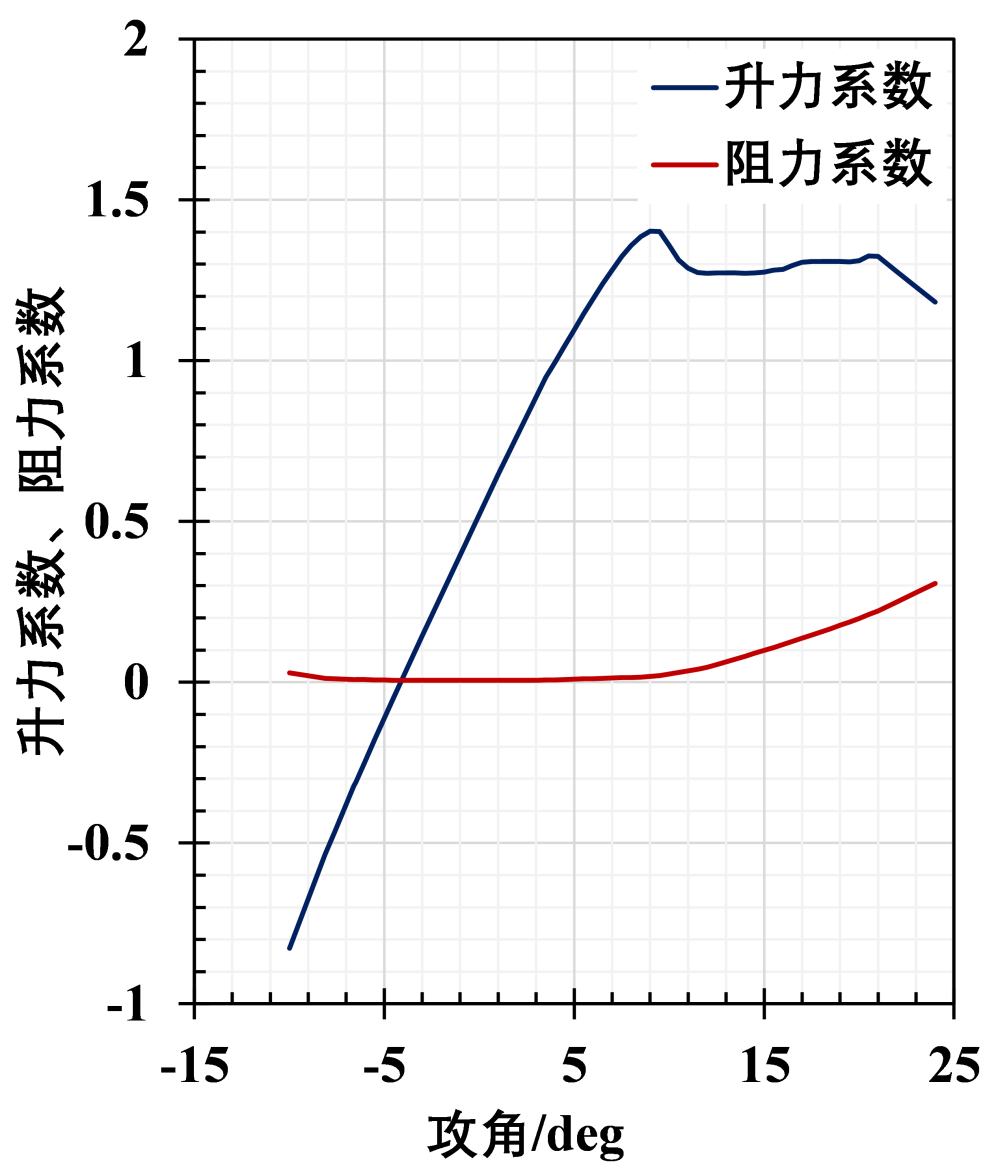
那么转速和桨距角是如何影响攻角的呢?
攻角的数学定义是工质入流方向与翼型弦线的夹角,弦线就是翼型前缘点与尾缘点的连线。弦线与风轮旋转平面的夹角称为扭角,入流角则是相对风速与风轮旋转平面的夹角。
下为一个典型风电叶片翼型速度/气动力三角形示意图,其中V为入流风速。由于风轮旋转会产生一个局部线速度(Ωr),所以最终作用在翼型上的速度为W,也就是相对风速。
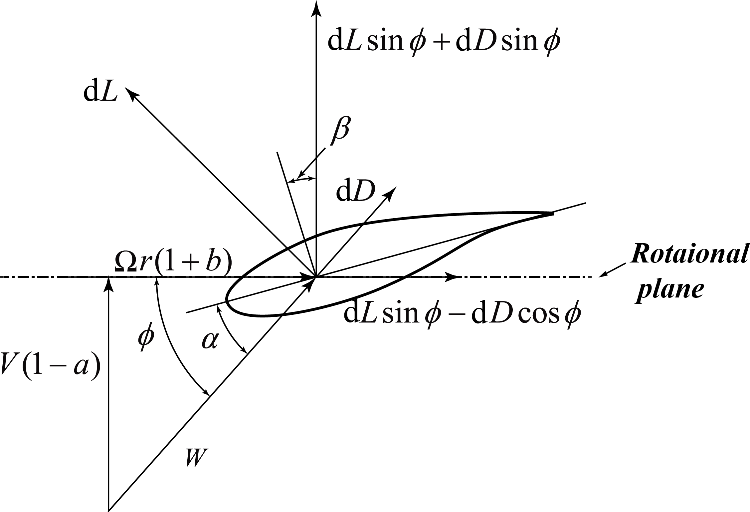
注:其中系数a、b为诱导因子
显然,攻角不仅受到入流风速的影响,还受到风轮转速的影响。
那么桨距角跟攻角关系的呢?
入流角φ=桨距角θ 扭角β 攻角α。
上面这个图中,没有表示出桨距角的定义。桨距角是针对整个叶片的。在风电机组实际运行中,可以通过致动器让叶片局部扭转,使上图中的翼型顺时针或逆时针旋转。这就是桨距角控制,其中顺时针为负(让压力面对风),逆时针为正(让前缘点对风)。

所以,通过调整风轮转速或桨距角大小,都可以通过改变叶片攻角控制气动载荷,让机组的气动效率维持在一个合适的气动效率范围。
二、变速还是变桨?
从上面我们知道,当相对风速大小或方向变化时,攻角随之变化,引起气动载荷的变化。我们可以通过调整转速或桨距角,实现气动载荷的控制目的。那么什么时候选择变桨,什么时候选择变速呢?
这里,我们先介绍另一个关键概念:尖速比。
尖速比(Tip Speed Ratio,TSR),也就是叶尖速度与入流风速的比,数学定义为:Ωr/V。通常用希腊字母λ表示。
当风速不变的时候,风轮在不同的转速下气动效率一般如下图所示。

其中,气动效率最大值对应的尖速比称为最佳尖速比。一般大型风力机的额定风速在11m/s左右,设计最佳尖速比都在7.0~8.0左右。主要原因之一是为了让叶尖速度尽量不超过100m/s,避免过大的叶尖噪声、叶尖振动和可压缩流动等问题。这也是为什么越大的风电机组,额定转速越低的原因之一。
当风速低于额定风速时,此时风的能量不够大,我们应该尽可能的多发电,让风力机以最佳尖速比运行,从而保持最高的气动效率。根据尖速比的定义,我们可以根据当前风速,计算出对应的最佳转速,实现合理的转速控制。
当风速高于额定风速时,此时风的能量较大。如果依然以最高气动效率状态运行,那么输出功率将会高于额定功率,也就意味着叶片和塔架要承受比设计值更大的载荷。为了结构安全,我们需要降低气动效率。所以,这时候可以通过增大桨距角,减小叶片气动升力,降低整机气动效率,同时保证额定功率输出。
三、转速控制实现方式
桨距角控制的实现方式很好理解,就是在叶根处安装电机,通过电机带动叶根齿轮转动,实现叶片扭转,从而控制叶片桨距角。
那转速呢?首先需要特别注意的一点是,虽然前面在解释转速控制对气动载荷影响的过程中,转速指代的是风轮转速,但是我们在控制器中,转速一般指发电机转速。
由于风轮转轴与发电机转轴中间连接着一个变速箱,忽略风轮转轴的扭转变形效应,发电机转速与风轮转速成线性比例关系。因此,控制发电机转速,等同于控制了风轮转速,从而实现了气动载荷的控制效果。
需要特别注意的是,转速并不是直接控制变量,发电机扭矩才是(注:文中扭矩和转矩均指代torque)。转速控制实际上是通过调节发电机输出扭矩实现的。通过调节变流器功率器件的脉宽,可以实现发电机扭矩的输出控制。
四、传动系统动力学方程
我们的需求是控制发电机转速,但是实现方式是调节发电机扭矩。如何通过调节发电机的扭矩去改变发电机转速呢?
忽略风轮转轴的扭转变形,基于牛顿第二定律,可以建立传动系统转动方向的动力学方程:
![]()
其中Tr是风轮气动扭矩,Tg是发电机扭矩,Ng为齿轮箱变速比。Jgt为传动系统的转动惯量, 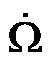 这哥们就是发电机转轴的转动加速度了。
这哥们就是发电机转轴的转动加速度了。
从这个方程中,可以发现,转动加速度直接受到发电机扭矩Tg的影响。
调低Tg,那么转动加速度大于0,转速增大;调高Tg,转动加速度小于0,转速就会减小。
基于当前风轮气动扭矩的大小,以及转速控制的目标,就可以适当的调节发电机扭矩的大小,实现转速控制。
五、控制区间划分
根据转速大小,控制器一般可以划分为5个区间。下为NREL 5MW风力机的控制区间划分,包括区域1、区域2和区域3以及2个过渡区。
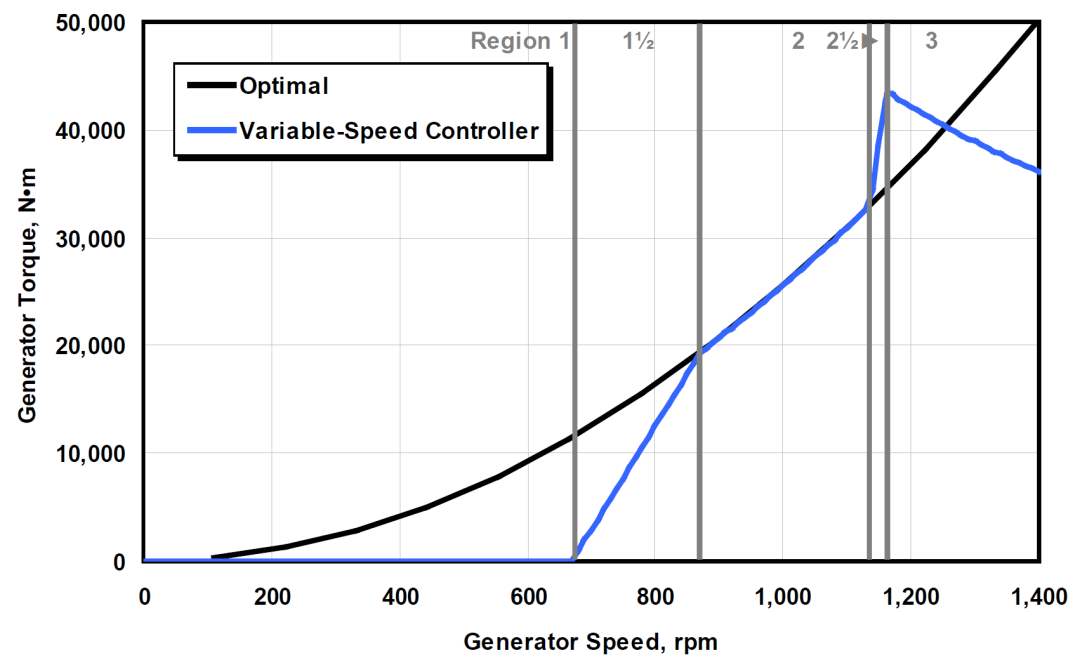
注:黑色的optimal曲线就不用管了
其中区域1发电机目标转矩为0,转速较低,发电机不输出功率。主要对应低风速区。若风速高于切入风速,则发电机会慢慢加速,经历区域1的整个过程,直至达到设定的最低发电转速,进入第一个过渡区:1-1/2。
在这一过渡区内,要让风力机迅速进入到区域2(高效发电区)。两点之间,线段最短。所以这个区间内,扭矩随转速线性增大。环境风速只要大于切入风速,风力机在开机的过程中,都会经历这一阶段。
在区域2中,风力机以最佳尖速比运行,保持最高的气动效率,尽可能多发电。当环境风速处于切入风速与额定风速区间内时,风电机组可以长时间处于这一控制区间内。此时,发电机扭矩与转速的平方成正比。
为什么是平方呢?我们来简单推导一下。
首先,风的动能与风速V的三次方成正比。在这一区间内,气动效率最高为Cp,所以发电功率可以表示为:
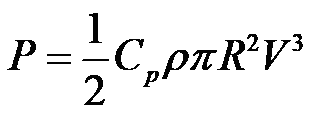
根据尖速比的定义,将风速V转化为转速。同时功率又等于扭矩与转速的乘积,即:
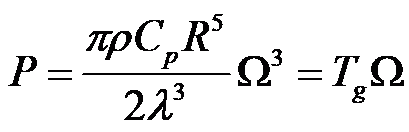
很明显,此时发电机扭矩与转速二次方成正比,为:
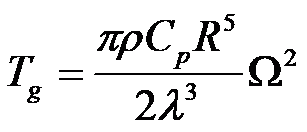
这个系数可以记一下,采用NREL 5MW风力机设计报告中采用的转速-转矩控制方法时,这一系数就是区间2的关键控制参数。注意转速的单位为rad/s
区域3则表示高转速区域,此时环境风速一般高于额定风速,可以输出额定功率,但同时需要启动桨距角控制。
这一区间内,一般可以分为定功率控制和定扭矩控制两种模式。
定功率控制时,目标扭矩与当前转速成反比;定扭矩控制时,目标扭矩为额定扭矩,即额定功率除以额定转速;为了功率输出稳定,一般风电机组均采用定功率控制。对于海上风电机组,也是如此。
因为浮式风电机组出现的比固定式基础要晚,所以最开始对于浮式风电机组的控制,直接采用固定式基础风电机组的控制。对一些特定的平台,会出现横摇或纵摇大幅度震荡的问题。这主要是因为控制器的频率与平台纵摇/横摇频率比较接近,气动力的变化频率与平台固有频率接近,而发生共振现象。
这时候可以改为定扭矩控制,会一定程度上改善这一现象。其背后的机理是避免气动阻尼过度降低,引起系统运动响应震荡。但还是治标不治本的,控制频率和固有频率接近的话,还是会引起共振。
所以,更好的方法是改变桨距角控制参数,调低控制器频率,使其明显小于平台固有频率。这一过程也被称为控制器解调(Controller detuning),也就是降低比例增益和积分增益。
因为浮式风电机组具有较大的纵荡和一定的纵摇,在风的作用下,会向风的同方向运动。从而降低了相对风速,这时候,即使不采用变桨控制,气动扭矩也会因为相对风速的下降而降低。
如果依然保持高频率的控制,就会让风电机组的气动阻尼过度下降了。平台在恢复刚度的作用下迅速迎风运动。反而会导致平台产生更大的运动范围。
调低控制频率,感觉是让控制系统变得“迟钝”一些,引起的迟滞效应通过平台本身的运动进行补偿,让风电系统维持在一个相对稳定的运行状态。
这也是为什么固定式基础的控制器必须要解调之后,再用于浮式风电机组的主要原因。
六、变桨-变速控制模型
采用NREL 5MW风电机组设计之初所采用的控制方法,转速的控制比较简单,只需要定义好前四个区域过渡点的转速和对应的扭矩即可。
比较困难的是建立变桨控制模型。
我最开始编程的时候,我导师跟我最常说的一句话就是:数学家已经证明了,只要给定输入和输出,加上逻辑、判断和循环三种结构,任何一种系统都可以通过程序表示。
当时只记住了前面一句:给定输入和输出。这句话让我受益匪浅。之后无论是处理什么类型的问题,只需抓住主要矛盾:输入和输出,就有思路了。
那么咱们变桨控制系统的输入和输出是什么呢?
很明显,输出是桨距角。输入其实可以有很多,所有会影响气动力的变量,都可以作为控制系统的输入,比如叶片振动速度、塔顶振动速度、平台运动速度等。但一般都会包括发电机转速,因为无论变桨或不变桨,都需要转速信号输入,调整发电机扭矩。
NREL这个报告里面,则只采用了发电机转速。那么接下来,我们需要构建一个叶片桨距角与转速之间的数学模型,即:转速是以何种方式、何种程度影响桨距角的。
我们通过分析NREL报告里面的方法,来简单理解一下变桨系统的开发思路和流程
(这个方法其实最早是Bossanyi在UpWind项目中提出来的,Jason大兄写这个报告的时候,没有引用那个文献,可能是觉得读者都对这个方法/文献比较熟悉)
经过简单分析,我们可以发现桨距角与转速二者之间没有直接联系。但是二者都会影响气动性能,气动性能参数包括功率、推力和扭矩。其中,功率又可以表示为扭矩乘以转速。而气动扭矩与发电机扭矩还会影响转速(见传动系统动力学方程)。
所以,扭矩就是联系桨距角与转速的一个完美变量。
首先,气动扭矩Tr和发电机扭矩Tg分别可以表示为:
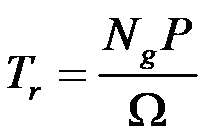
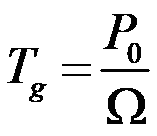
Ng是齿轮箱增速比,Ω是发电机转速,P为气动功率,P0为额定功率(区域3此时发电功率为定值,即额定功率)。
发电机扭矩是转速的函数,气动扭矩是桨距角的函数,对这两个方程分别基于转速和桨距角进行一阶泰勒展开,得到:
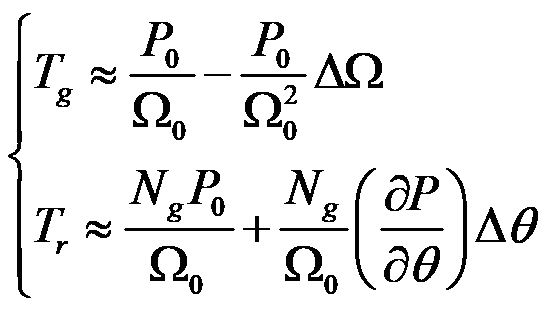
桨距角增量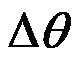 可以表示为转速增量
可以表示为转速增量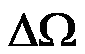 的比例积分微分(Proportional-Integral-Derivative,PID)形式,也就是常说的PID控制:
的比例积分微分(Proportional-Integral-Derivative,PID)形式,也就是常说的PID控制:
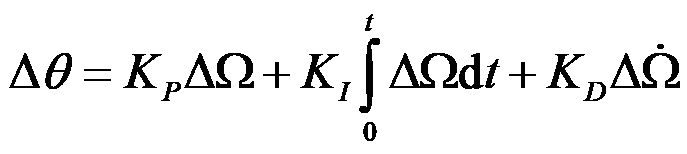
Kp、KI和KD分别为比例增益、积分增益和微分增益,是这个控制链中最重要的三个参数,,确定了他们的数值大小,也就完成了控制系统的开发。
由于微分项会增加控制系统的惯性,所以对扰动的输入信号十分敏感。当输入信号的时滞较大或系统惯性较大的时候,微分控制比较有效,但对于扰动较大的输入信号,微分项容易引起控制系统的震荡。由于风轮转速时刻变化,一般会忽略微分项。
所以我们常见的风电机组桨距角控制器一般都是采用PI控制,只保留了比例项和积分项。
将PI形式的桨距角方程和气动扭矩/发电机扭矩的泰勒展开式,带入到传动系统的动力学方程(![]() )中:
)中:
可以得到:

这个方程实际上是一个二阶方程,只需要把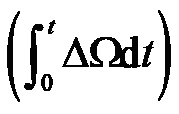 看成一阶变量,令
看成一阶变量,令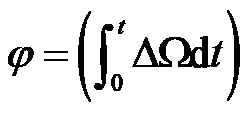 ,那么
,那么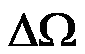 就是φ关于时间的一阶导数。所以上面这个方程可以表示为:
就是φ关于时间的一阶导数。所以上面这个方程可以表示为:
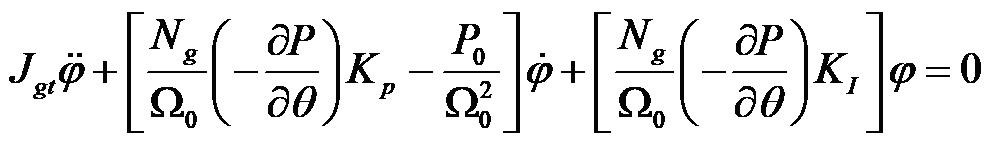
从上式中可以发现,该控制器中存在一个负阻尼项(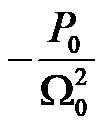 ),需要通过比例Kp项进行补偿。
),需要通过比例Kp项进行补偿。
将上式换成质量M、阻尼C和刚度K,则可以表示为:
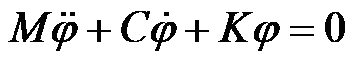
控制器频率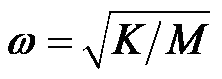 ,阻尼比
,阻尼比
Hansen建议,在进行Kp数值计算时,忽略负阻尼项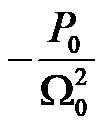 。原因他没说,但是我感觉可能是为了让桨距角变化更平缓一些。因为如果考虑这个负阻尼项,那么Kp值会更大。桨距角变化就会更剧烈一些,对系统运动/振动稳定性不是件好事情。
。原因他没说,但是我感觉可能是为了让桨距角变化更平缓一些。因为如果考虑这个负阻尼项,那么Kp值会更大。桨距角变化就会更剧烈一些,对系统运动/振动稳定性不是件好事情。
在忽略负阻尼项的情况下,可以将比例增益和积分增益分别表示为:
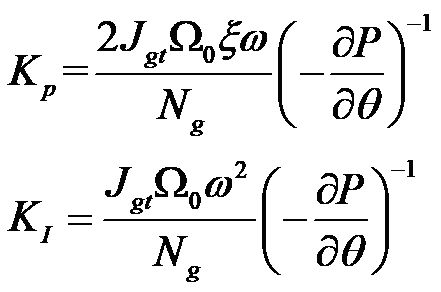
上面公式中的未知数有三个:控制器频率、阻尼比和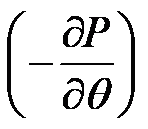 。控制器频率和阻尼比一般直接赋值,
。控制器频率和阻尼比一般直接赋值,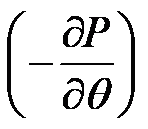 这个变量是气动功率关于桨距角的偏导数(忽略负号),表示某一桨距角下功率对桨距角的敏感度(下称:功率敏感度),与风轮转速、风速和桨距角有关,需要手动计算。
这个变量是气动功率关于桨距角的偏导数(忽略负号),表示某一桨距角下功率对桨距角的敏感度(下称:功率敏感度),与风轮转速、风速和桨距角有关,需要手动计算。
我们知道,在高于额定风速区域,功率为定值(额定功率),稳态桨距角逐渐增大,如下图所示。
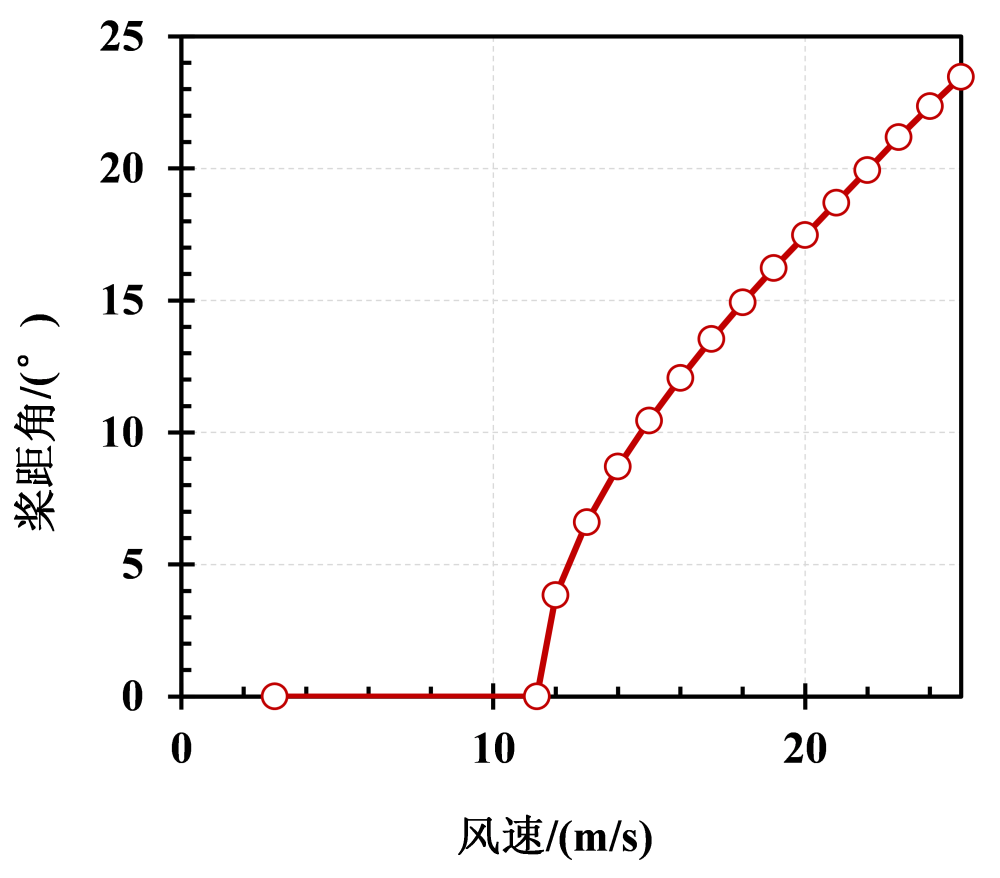
可以通过FAST软件或AeroDyn计算风电机组在某一风速条件下,桨距角在对应稳态桨距角附近时的气动功率,拟合气动功率-桨距角曲线,即可得到该桨距角下的功率敏感度。
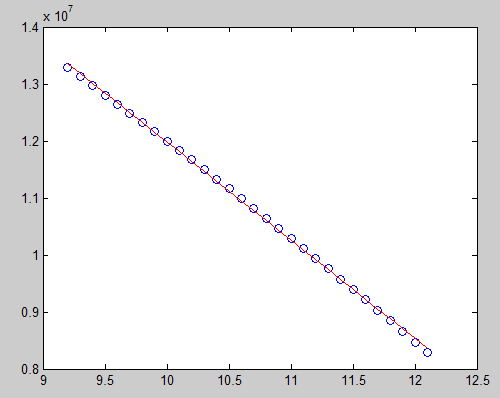
重复这一步骤,即可得到不同桨距角对应的功率敏感度。NREL通过一次函数拟合了功率敏感度与桨距角的变化关系,结合0°桨距角下的功率敏感度,便可以得到任意桨距角对应的功率敏感度。

定义桨距角控制频率和阻尼比分别为0.6 rad/s和0.65,就可以得到该风电机组桨距角控制器的增益调度方案。
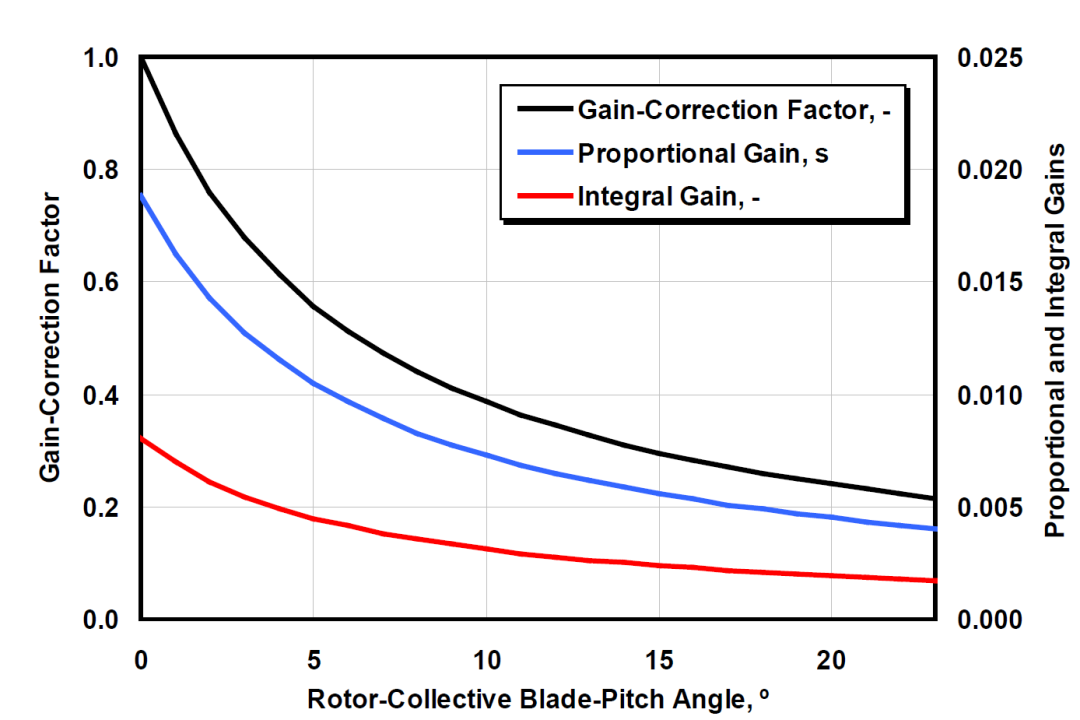
增益调度,也就是不同桨距角下的增益修正,是风电机组桨距角控制器设计中十分重要的一步。NREL控制器是通过一次函数拟合增益修正系数,DTU控制器通过二次函数拟合,而开源的ROSCO控制器则是通过定义不同桨距角下的增益,仿真过程中通过查表插值获取对应的增益。
仿真过程中,基于输入的实时发电机转速信号和设定的目标转速之间差距(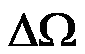 ),通过PI方程计算桨距角增量
),通过PI方程计算桨距角增量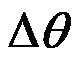 :
:
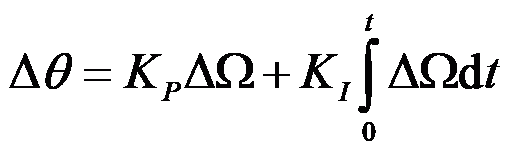
至此,桨距角控制器设计已基本完成。
七、滤波器
风电机组转矩-桨距角控制器,除了设定各个控制区域的转速、目标转矩和桨距角控制增益等重要参数之外,另一个十分重要的步骤是滤波器设计。
如前所述,转矩-桨距角控制器的输入信号为发电机转速。该变量为风力机气动-水动-伺服-弹性全耦合仿真的计算结果,受到气动载荷、波浪载荷、结构振动和控制器等因素的影响,所以在转速信号中,除了最为显著的风轮旋转频率分量之外,必定会包含叶片振动频率、塔架振动频率、风浪激励频率、控制器频率等分量。
为了避免这些额外频率分量对转速信号的干扰,一般需要采用滤波器,将这些分量与转速信号尽量分离开。
在NREL的默认的控制器中,仅采用了一个低通滤波器(low-pass filter),截止频率设定为1/4一阶叶片摆振频率,约为0.25Hz。也就意味着,高于这一频率的分量,包括叶片挥舞、叶片摆振、塔架弯曲等模态的振动频率分量,大部分能量会被过滤掉。
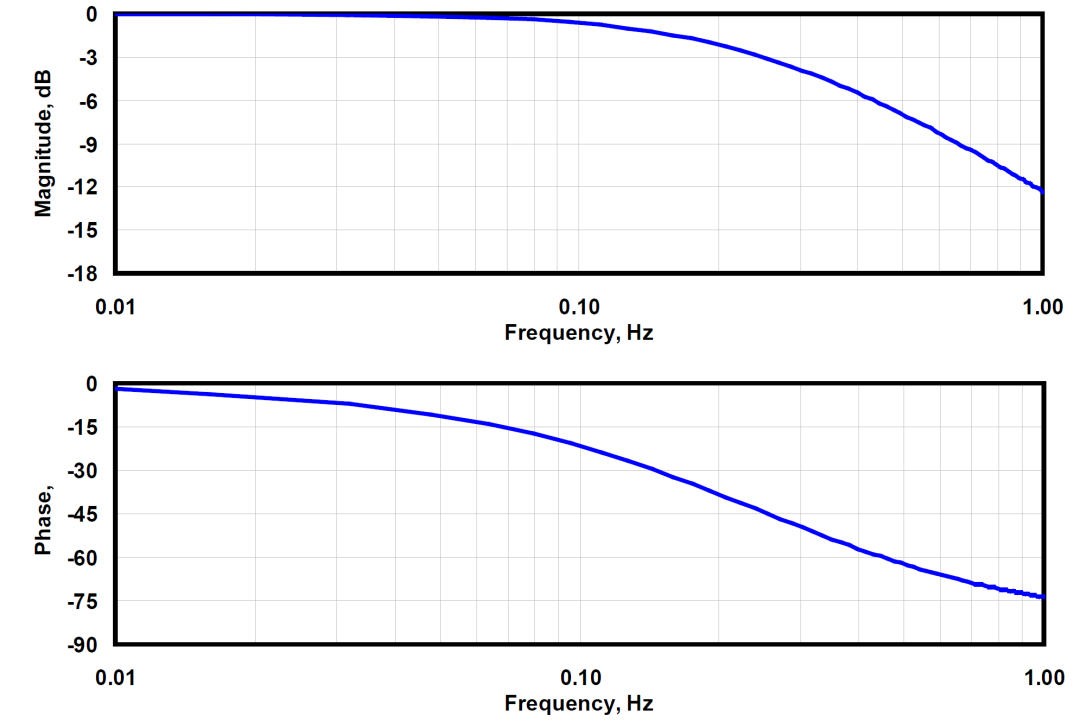
对于浮式风电机组,平台纵摇/横摇固有频率较低,这一频率可以顺利通过低通滤波器,这时候可以采用窄带陷波滤波器(Notch filter)针对性的过滤这一低频信号,避免共振。
ROSCO控制器即提供了这一功能,通过定义Notch滤波器的过滤频率和宽度以及阻尼,实现窄带信号的过滤。
八、写在最后
风电机组控制器开发设计是一项十分复杂且极具难度和挑战的工作,意义十分重大,其性能直接决定了机组动态性能的优劣。
本文仅介绍了一种常规的简单控制器设计方法以及控制器工作的基本原理。由于本人非控制专业科班出身,水平十分有限,其中关于控制器开发的部分,定然有不妥之处,还望各位专业读者海涵,不吝指正。
(完)




