应用Code_Aster模拟核电阀门在热冲击下的热力学响应

Code_Aster是法国电力集团(Electricité de France,EDF)自1989年起自主研发的一款通用计算固体力学开源软件,其中“aster”是法语“用于学习与研究的结构与热力学分析”的首字母简称(Analyse des Structures et Thermo-mécaniques pour des Etudes et des Recherches)。Code_Aster可以提供全系列的多物理场分析和建模方法,其功能远远超出了标准的热-力计算代码。该软件包含多种本构关系模型(弹性、弹塑性、弹粘塑性、辐射下的燃料棒和金属等),能够处理线性和非线性问题(接触、摩擦、断裂力学,地震分析等),同时也可被用于土木工程结构的性能分析,微观尺度的晶粒计算,几乎涵盖了核工业涉及的所有固体力学应用领域。该软件的模型、算法和求解器自面世以来一直在不断地提升和完善中。2008年末,法国电力集团将code_aster与图形操作模块整合,开发出了用户界面友好的开源软件Salome_Meca,使得Code_Aster在使用代码处理研究数据的基础上,实现了可视化图形操作功能。
研究背景
在核电站中,核电阀门是保障核电站正常运行的重要构件,对核电阀门的检验则是核工业中的重要项目。阀门的密封性、可操纵性是检验的关键指标,具体的检验方法和依据包括实验测试、使用者反馈、数值模拟、理论计算等。相关供应商负责提供包括有限元数值仿真结果在内的证明文件,而法国电力集团方面必须有能力对这些文件进行鉴定,即评估其数值仿真结果是否可信。因此,对于法国电力集团,应用公司自主开发的Code_Aster对像核电阀门这样的关键部件进行数值模拟是一项必要的工作内容。
2015年,在与加拿大威兰阀门公司(Velan)签订合作协议后,法国电力集团在其位于位于枫丹白露的Les Renardières实验室中进行了多项试验。本期文章涉及的试验是对一种高度仪器化的轻维护阀门进行的测试,获取了温度、螺栓紧固力、法兰开口测量值和试件残余变形等数据;同年,五名工程师和一名实习生使用Code_Aster完成了对该阀门的数值模拟;2016年,在比对实验结果和第一次数值模拟的结果后,对数值模拟进行了二次优化;2017-2019年,分别针对管道内流体流速、阀门尺寸对实验结果的影响以及阀门的简化建模方法进行了研究。
本研究的目的是将测试期间获得的数据与经Code_Aster得到的多物理场数值模拟结果进行比较,评估数值模拟的可信度与局限性。
实验条件
本案例中所研究的阀门是一个带有可移动阀笼和阀座的阀门原型机(见图1)。阀体与阀帽间由12个规则间隔的螺栓固定以保证其密封性。图2着重呈现了数值模拟中阀体和法兰处的不同构件。水在阀门主体与阀笼之间以及阀笼与阀座衬层之间的间隙中循环并渗透,填充了阀帽与波纹管之间的空间。阀门的下部由绝热层覆盖,上部则与自由空气相接触。

图 1. 实验中的阀门试件与其在数值模拟中的不同构件
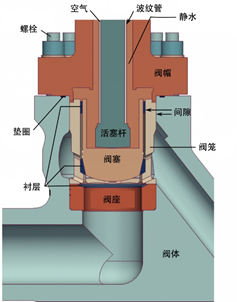
图 2. 阀门细部剖面示意图
实验中对阀门施加的热冲击如下:在阀门处于高温热平衡状态下(285℃)时注入冷水(60℃),静置数小时至其达到低温下的热平衡状态;再注入热水(285℃),静置数小时使其达到高温下的热平衡状态,如此进行14次温度的交替变化。阀门中设置有37个热电偶,用于测量阀门各处的温度。阀帽处法兰的12个螺栓同样设置有热电偶和应变仪,用于获取螺栓温度与紧固力随时间的变化。
对此实验的模拟包括流体力学、热力学和力学三部分。流体力学部分在code_saturne上完成,本文讨论的热力学和力学部分在Code_Aster上完成。我们利用试件的对称性,在建模中仅模拟了结构的1/2;对于热冲击,忽略多次热冲击所造成的累积残余变形,仅关注试件在一个285℃ – 60℃ – 285℃温度交替变化作用下的热力学响应。热力学模拟所得到的温度变化结果作为外力条件用于力学计算中,从而得到阀门中不同构件的应力与变形情况。
热力学分析部分
热量的传递包括传导、对流和辐射三种基本形式,本案例中仅涉及前两者。在2015年进行的第一次数值模拟中,我们假定各部件紧密贴合,不考虑管道中流体流动性所造成的对流传热,热量在阀门内部完全通过接触传导方式传递;在第二次数值模拟中,增加了“阀体与阀笼之间的间隙中热量以对流方式传递”的边界条件。
经模拟,对于阀门中的绝热构件,模拟结果与试验结果匹配度良好;对于螺栓,第二次的模拟结果改善了第一次模拟中温度变化较试验结果有所延迟的问题(图3)。阀门上部的温度较试验结果高约30~40℃(图4),这可能是模型相对简单,未充分考虑其他形式的传热方式导致的。
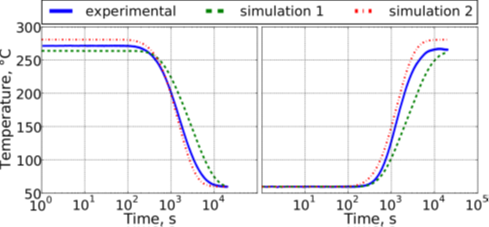
图 3. 实验与数值模拟中阀门螺栓温度随时间变化曲线
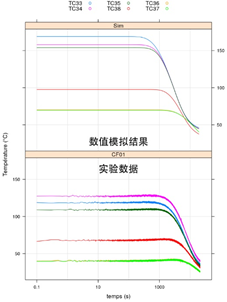
图 4. 实地实验与数值模拟中阀门上部温度随时间变化曲线
(285℃ →60℃阶段)
力学分析部分
在模拟分析阀门的力学特性时,重新划分了有限元单元。单元形式由热力学分析中四面体单元改为四面体单元和线性六面体单元组合的形式(图5)。


图 5. 热力学分析(左)与力学分析(右)中阀门附近的有限元网格划分
在施加热冲击前,处于室温20℃下12个螺栓的紧固力均为250kN。力学分析部分的模拟共历时约17小时,其中仅考虑弹性状态历时约7小时,考虑弹塑性状态历时约10小时,两种工作状态下螺栓的紧固力随时间的变化如图7所示。虽然一次热冲击周期下两种工作状态所得到的结果相似(图6),但针对试件残余变形的分析,考虑其弹塑性工作状态是必要的。
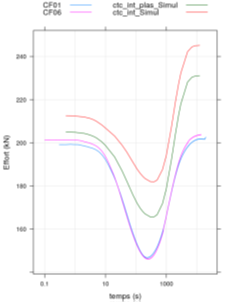
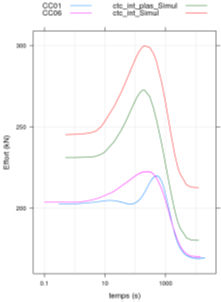
图 6. 弹性与弹塑性工作状态下螺栓的紧固力随时间变化曲线
(红色:弹性;绿色:弹塑性)
图7为285℃à60℃阶段t=350s时模型中的温度场,此时第二次模拟得到的螺栓紧固力最小。我们注意到,在第一次模拟中,热冲击由底部开始,同时穿过阀帽和螺栓,二者的温度变化可以说是同步的;在第二次模拟中,热冲击则由内部开始并向外扩散,在到达螺栓前先穿过阀体与阀帽之间的空隙并直接影响阀帽的温度。第二次模拟还原了实验中阀帽与螺栓热膨胀延迟的现象,即在注入冷水阶段螺栓松动,在注入热水阶段螺栓过紧。

图 7. 模拟1(左)和模拟2(右)在冷水注入阶段阀门处的温度场
由于未考虑实验中紧固力的离散误差 ,数值模拟中6个螺栓紧固力的平均值较实验值高约30kN。同时我们注意到,在(图8)2016年进行的第二次模拟中,螺栓的紧固力在285℃→60℃(图8左)与逆向的60℃→285℃(图8右)过程中存在与实测结果相似的降低和升高趋势。
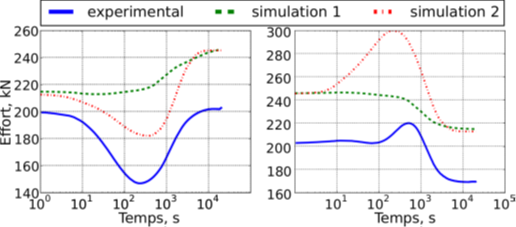
图 8. 实地实验与两次数值模拟中螺栓紧固力随时间变化曲线
结论
1. 两次模拟结果的差异表明,考虑阀门部件间隙和流体以对流方式传热时得到的热学与力学响应结果与实验结果,特别是螺栓的紧固力,拟合度更好;
2. 相较第一次模拟,第二次模拟中阀门下部区域的温度与实验结果拟合度较好,而上部区域的温度拟合度较差。
更多资讯可登录格物CAE官方网站
远算在bilibili、知乎定期发布课程视频等内容
敬请关注




