从双球模型看MatDEM中的离散元原理
在MatDEM中有一个双球碰撞的案例,执行文件名为user_TwoBalls.m。这个例子构造简单,非常适合用于初学者探究MatDEM中离散元的原理。运行后的结果如图1所示,图1中的两个活动单元是被胶结在墙单元上,基本没有运动。下面通过这个案例对MatDEM中的阻尼机制,胶结原理进行探究。
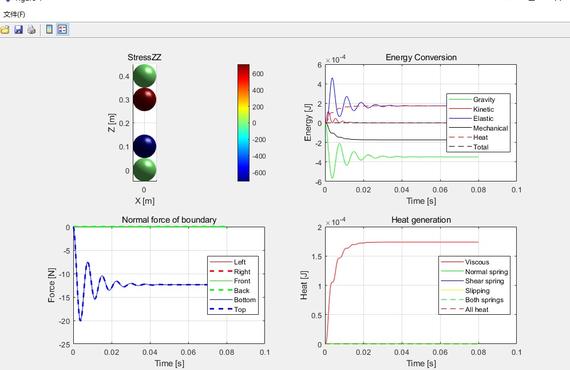
图1
首先对离散元原理进行简要概述。MatDEM中的接触模型很简单,在切向和法向上各有一个弹簧来产生法向力和切向力,并且在切向有一个遵循莫尔库伦准则的滑动机制,具体公式见式1[1]。式1中有一个Xb需要特别注意,这个断裂位移是通过宏微观公式式2[1]换算得到的,这个断裂位移乘以等效刚度就是d.mo.aBF矩阵中的断裂力,拉力大于这个值时胶结断裂。
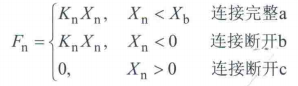 (1)
(1)
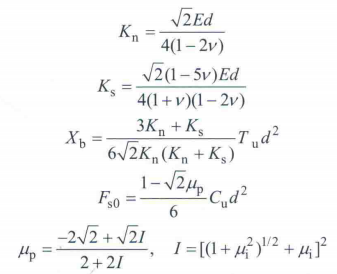 (2)
(2)
关于阻尼机制,相当于给活动单元一个与运动速度相反方向的力耗散活动单元的能量。有一点需要注意,MatDEM中忽略颗粒的旋转,所以在MatDEM中接触力是不存在弯矩力的,这就导致MatDEM无法对一些具有抗弯特性的材料进行模拟,如钢铁、塑料等。
这里建立的双球碰撞模型是在模型箱的框架下,用d.addElement命令导入四个小球的。在该模型中小球半径都为1m,重力统一为2000N。通过设置d.vRate(阻尼系数)的值来模拟有无阻尼的情况。d.vRate=0时,结果如图2所示,右边图为两小球的Z坐标变化情况。d.vRate=0.001时,结果如图3所示。留个思考,如果d.vRate=1会是什么结果呢,可以自己试试。将两图进行对比就会发现有阻尼时,两小球很快就会稳定下来,而无阻尼两小球会一直上下弹跳下去。由图2中的曲线图也会发现在两球碰撞激烈时间段,曲线越不平滑,这是由于时间步过大造成的。
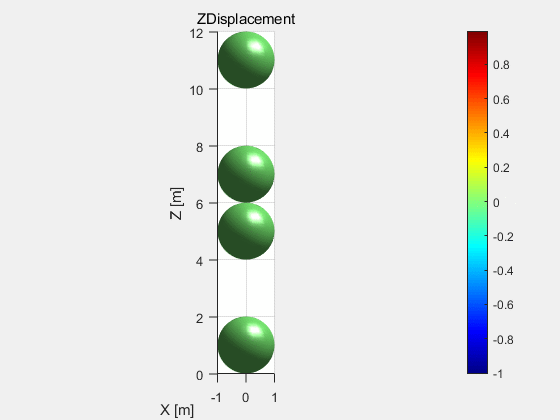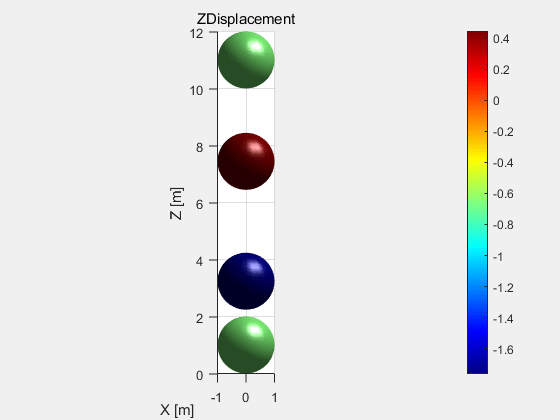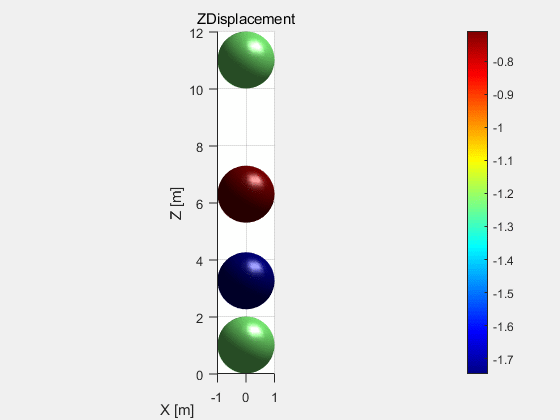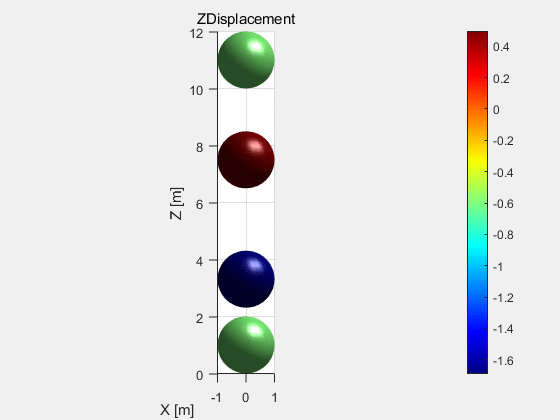
图2
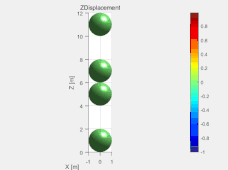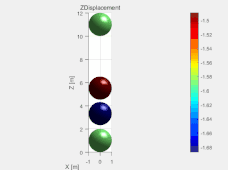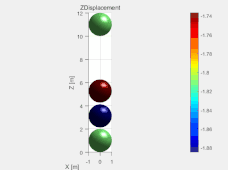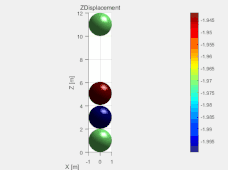
图3
再对胶结情况进行探究,这里直接简单粗暴,将胶结矩阵设为d.mo.bFilter(:) =true,将断裂力矩阵设为d.mo.aBF(1:d.mNum,1)=2e6,设置远大于重力2000是由于时步的选取问题。得到的结果如图4所示。对比图2可以看出两小球胶结在一起没有分离弹开。(笔者水平有限,如有出入,欢迎指出)
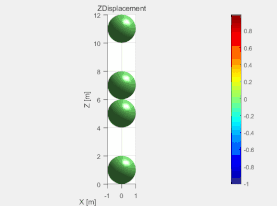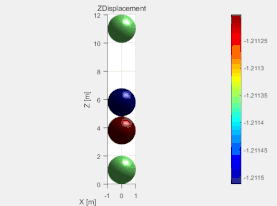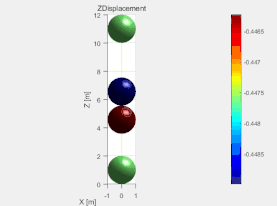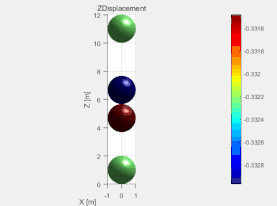
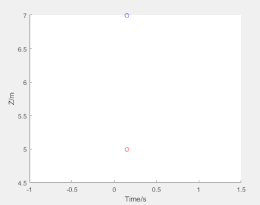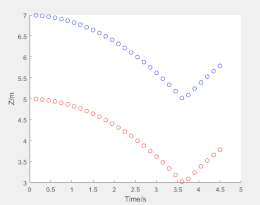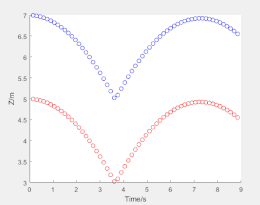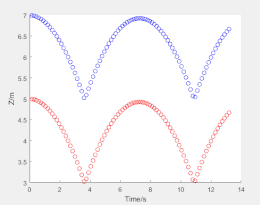
图4
参考文献
[1] 刘春. 地质与岩土工程矩阵离散元分析[M]. 北京: 科学出版社, 2019.




