等参变换——学习笔记

一本英文的有限单元法教材。
翻译一小段英文书,随便讲讲等参变换。
文前声明,这是一篇学习笔记。
虽然等参变换已经是有限单元法里面最基础的概念之一,我之前早已学过,甚至翻来覆去学过好多次。但这次读到相关英文教材的相关段落,就顺带着翻译一下。所以……前因后果什么的,写的少一点 请读者见谅。
在有限单元法里,我们知道每一种单元都有对应的形函数。但单元的形状千奇百怪。为了避免复杂几何情况下的繁琐推导,就需要坐标转换。
本文涉及的这本教材,我也不设置关键词回复了。下载链接在文末,我直接做成金山文档共享链接,都不用你从网盘下载。
等参变换
这本教材标题叫 Introduction to Finite Element in Engineering. 封面见推送头图。放在我的网盘里,啥时候下载的我自己也忘了。应该是从Pearson官方下载的吧。
我先跟着这本教材,大概讲一下相关章节。在PDF的328页,第九章。
整体模型被切成许多四面体单元,单元中的每个节点都有对应的编号,以及x,y,z坐标。下图就是一个典型的一阶四面体单元:

一个空间任意四面体单元
在这个单元里,我们定义四个形函数,叫它们 N_1, N_2, N_3, N_4. 每一个形函数N_i 在自己的节点(即第i个节点处)值为1,在其他三个节点上值为零。如图所示,N_1 在1号节点为1,在灰色的面上,值为零。
在标准单元(原文叫master element)上,可以这样定义四个形函数:
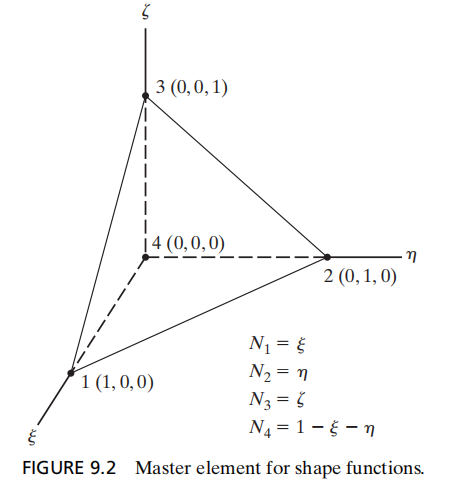
定义形函数的标准单元
这三个字母,ξ,η,ζ,注音格式分别写作\xi , \eta , \zeta,读作 ksi 克西、eit 艾塔、zat 截塔。物理学家们在坐标变换的时候总喜欢用这仨希腊字母,大家担待一下。
你看,把单元画成一个 由三个贴着坐标轴的直角三角形组成的四面体,定义形函数就非常方便。这样定义出来的形函数,完美满足上面说的要求。
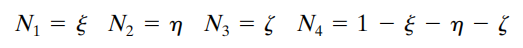
如果用 x_1, y_1, z_1 来表示1号节点的x,y,z坐标,以此类推,那这个形函数本身就直接可以用来描述从局部坐标系 (ξ, η, ζ) 到整体坐标系 (x, y, z) 的变换:
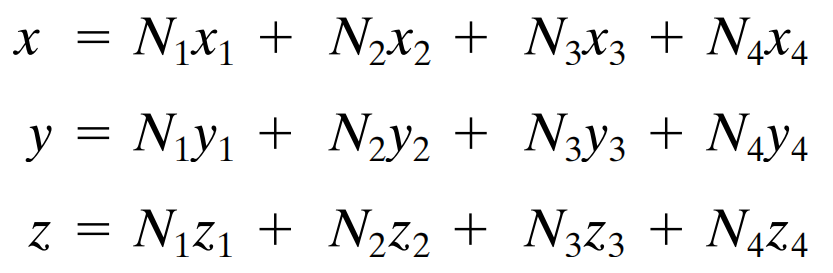
对不对,在1号节点对应的坐标处,N_1=1,剩下三个形函数都为零。其他三个点同理。
把N_i的表达式代入进去,再使用一个简化记法:

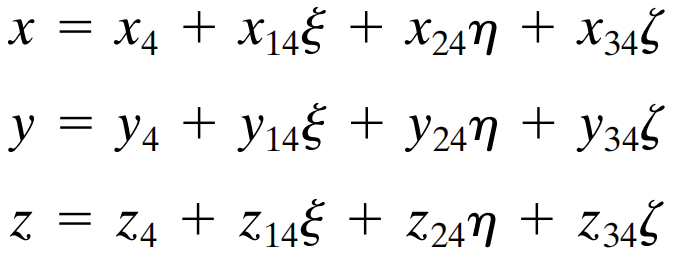
这就是从局部坐标系到全局坐标系的转换关系了。
根据位移求应变的时候,要对位移函数求导。使用链式法则,有:
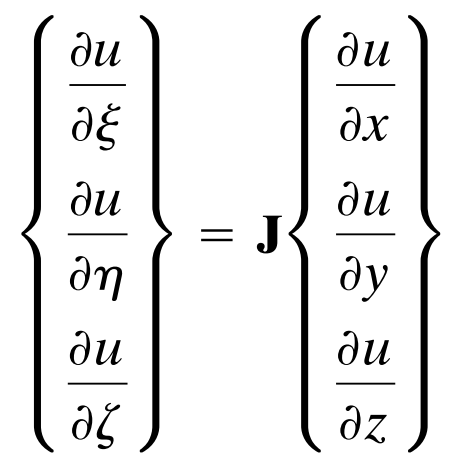
这里面的 J ,叫做雅可比矩阵 Jacobian matrix。这个名字被用来称呼由一大堆偏导数组成的矩阵。嗯。雅可比矩阵的系数也很容易就得出来了。
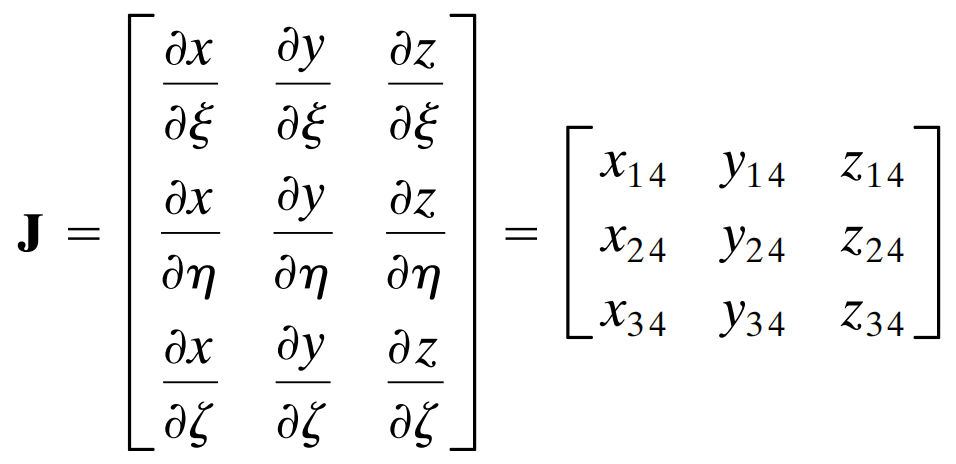
一般来说,雅可比矩阵的行列式 |det J| 表示坐标变换前后的体积改变量。由于标准坐标系下,那个单元的体积为1/6,所以变换后,在全局坐标系下,单元的体积为

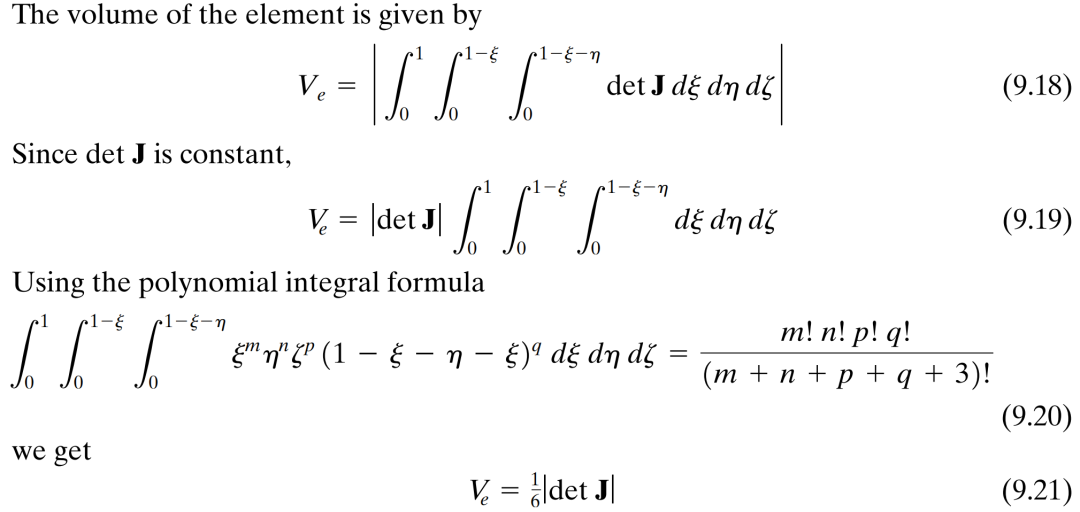
原书中还用了一个三重积分来计算标准单元的体积。
再进一步,我们想要的其实是刚才那个变换的逆变换:
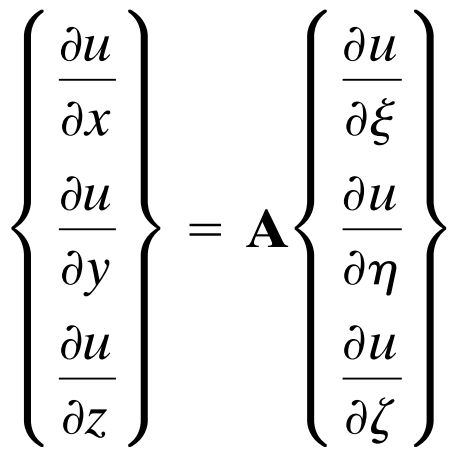
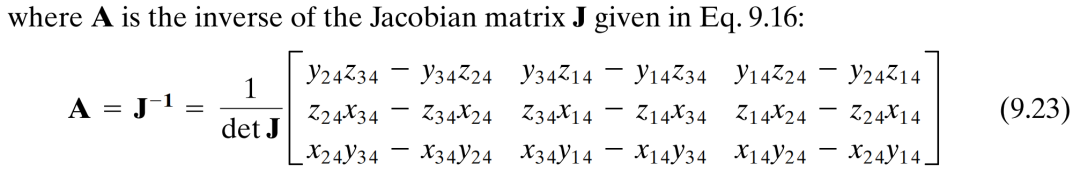
雅可比矩阵的逆矩阵就要稍微复杂一点。
再进一步,应变是位移的导数,在有限元里,把应变写成一个(6*1)的列向量,位移则是四个节点 每个节点三个自由度,一共(12*1)的列向量。那么
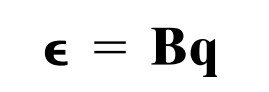
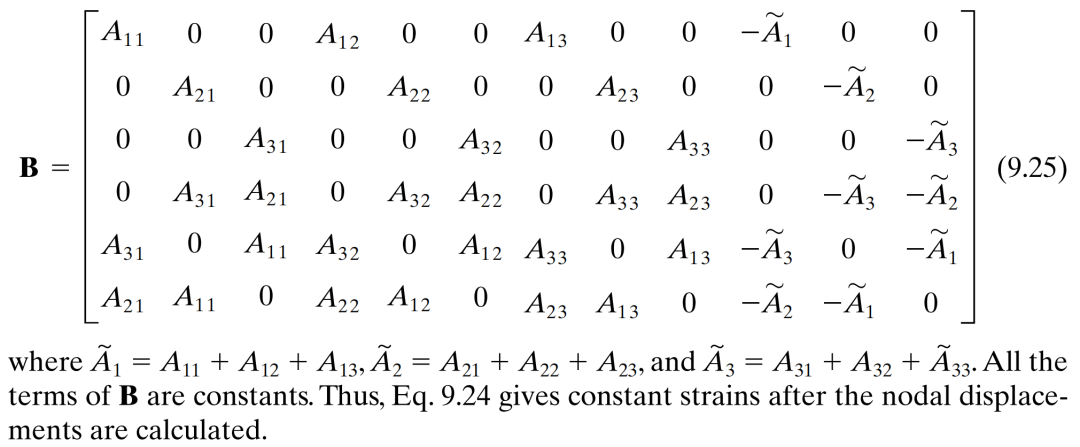
可以看出,单元形函数本来就是一阶,求过导数以后啥也没了就剩下常数。所以一阶四面体单元内应变为常数,一阶三角形和四面体单元被称为常应变单元。
在大家更熟悉的王勖成版教材中,等参变换的讲授方法略有不同。读过王勖成教材的同学们大概会对这张图片比较眼熟:
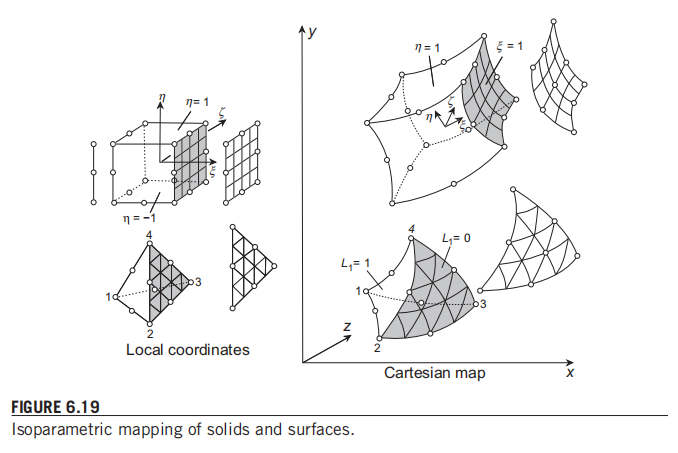
这是O.C. Zienkiewicz 教授的著名教材 The Finite Element Method: Its Basis and Fundamentals 书中第六章的配图。
看我心情,如果我自己有需要的话,过两天再把Zienkiewicz教授这本书的讲 法写出来。
本文电子书的分享链接:
【金山文档】 Introduction to finite elements in engineering (2012, Pearson)
https://kdocs.cn/l/caZD1BwZeeXr




