【科研分享】结构高阶模态的一点理解
文/心尘轩
网站/STKO OpenSees Software (asdeasoft.net)
做抗震研究时,我们不可避免会遇到一个问题:结构的高阶模态对结构的位移响应的 影响。那我们该如何认识高阶模态对结构变形模式的不利影响。一般而言,当我们在设计结构时,我们都期待结构沿着层高竖向刚度分布均匀,那么理想下,我们希冀结构的侧移变形呈现出结构一阶模态的分布,即类似于倒三角的变形模式。但是,现实是,尽管对于六层的结构,我们都可以发现结构在弹塑性下,并非是均匀的倒三角形式,结构的破坏往往是由于过多的变形集中于某一层(软弱层破坏)。此时,我们会很疑惑,我们在设计之处是严格按照竖向刚度是均匀分布的,为什么还会出现非预期的层间变形集中的软弱层破坏模式。要想解释这个现象,就得理解结构的高阶振型的影响。已有的研究表明这种影响在中高层的弹塑性状态尤为明显。
对于低多层结构,我们假定结构的动力响应完全可以由其一阶模态控制,即我们认为一阶有效模态质量即为结构的总质量,且假定结构在弹性和弹塑性下变形模式不改变,那么我们可以得出结构的在动力荷载下的响应也应该是均匀的,即按照结构的一阶模态分布。(当然上述的描述存在一个强假定,即低多层结构没有高阶振型影响,但事实证明即使是一个六层的结构,一阶振型对应的模态有效质量也很难达到90%以上,即高阶振型的影响不可避免,所以这里是假定的理想状态)。此外,还需要说明结构进入弹塑性状态后,一阶振型不改变的合理性。以下我们进行一个简单的理论推导,我们假定存在一个两自由度度体系,质量矩阵和初始刚度矩阵如下:
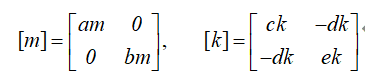
我们假定该两自由度体系在不同楼层处同时进入塑性状态,即体系的刚度同时衰减,此时结构的刚度矩阵可重写如下:

α为体系屈服后的刚度与初始刚度的比值。我们对屈服后的两自由度体系求其频率和振型,如下:
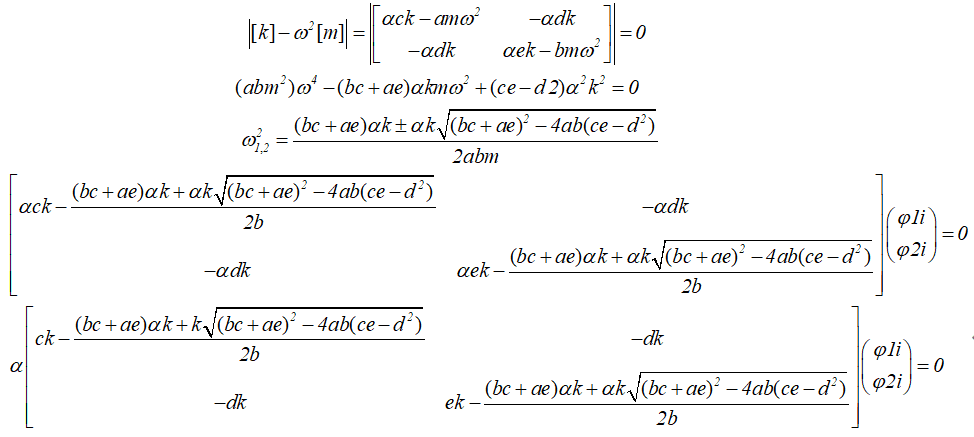
上述推导可见,体系进入塑性状态后,体系的频率显著下降,结构的周期显著增加,也即结构进入超“柔”状态,此时由动力学的知识可知,地震激励输入给结构的能量很有限(伪加速度A很小)。但是,观察上式,我们发现,结构刚度衰减系数α,对确定结构振型没有影响,即如果结构体系的刚度衰减一致(即结构层间刚度与相邻层间刚度比值保持不变),结构的振型在弹性和塑性时,是一致的。当然,我们要明白,我们设计的结构是否可以同时屈服,实在需要打一个问号。其次,一旦结构不是同时屈服,上述的层间刚度与相邻层间比值就会变化,那么结构的振型就会改变。所以真实的结构的响应是更加复杂。
上述讨论,得出的结论是,对于低多层结构,如果其动力响应完全由一阶模态控制,且结构各层同时屈服,我们可以认为结构在弹塑性状态下的振型不发生改变,且此时结构的响应是可以精确预测,且无层间集中变形的。
但现实告诉我们,上述的理想状态是无法实现的。首先,即使对低多层结构的动力响应也不完全由一阶模态控制。我们不得不面对高阶模态的影响,并正确做出相应的对策。
我们首先考虑结构在弹性状态的动力响应,由结构动力学理论可以得知,结构在弹性状态下,各模态之间是正交的,模态之间没有耦联关系,其第I 模态的结构反应不会在第J模态下产生任何响应。此时结构的动力响应可以由振型时程法可以求得,即:
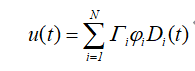
即结构的总反应等于结构N阶振型时程响应的叠加。这里给出几点说明,第一,结构在弹性范围内,尽管也存在高阶振型的对变形的贡献,但是结构的初始刚度较大,较大的刚度对结构高阶振型的峰值响应具有更有效的抑制作用(高阶模态较基本模态而言,周期短,相应较刚,且因其有效模态质量不大,因此,在弹性阶段内变形有限)。第二,结构是弹性的,整体弹性变形相对较小。但是,结构体系一旦突破进入弹塑性状态,其情况就变得较为复杂。比如实际上结构不可能在某一刻同时进入塑性的状态,因此,结构本身的模态随着结构各层塑性发展不同而有所改变,那么这种改变是否会使得各振型之间也不再满足正交性,即第I振型可以在第J振型发生反应,即振型之间开始耦联。所以,在结构的弹塑性阶段,结构高阶振型的影响包括两方面:高阶振型本身的贡献以及其在相邻振型的耦联。实际上,我们可以从这个角度来理解结构振型在结构首次屈服后出现耦联的本质,结构屈服后在新的层间刚度分布下,结构的模态已经稍微发生了改变,但是我们依然使用结构在弹性状态下的模态,这就可能导致结构在弹性状态下得到的振型在弹塑性状态开始存在些许耦联,即各振型已不再满足正交性。Chopra等研究表明,尽管结构出现显著的弹塑性状态,如果用初始的第N阶模态对应的力向量Peff,n(t)对结构体系进行非线性时程分析,并将结果分解在初始各振型空间上。结果发现,第N阶模态对应的力向量Peff,n(t)产生的位移不仅在第N阶振型上产生响应,在N阶振型以外的振型也产生了响应,这就表明结构一旦进入弹塑性状态,各振型就不再满足正交,此外,尽管N阶振型对应的力向量Peff,n(t)在N阶振型以外的振型上产生了响应,但是这些响应较N阶振型本身的的响应,可以忽略不计,即表明弹塑性阶段各振型是耦联的,但是这种耦联是较弱。因此我们依然可以像弹性状态下一样,认为结构在弹塑性状态下依然保持振型是正交的,基于此,结构的响应可以重写如下:
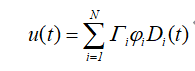
只是上式中的Di(t)表示为I阶模态的对应的非线性单自由度的位移响应。鉴于此,我们考量结构在弹塑性阶段的高阶模量影响,也可以像弹性阶段一样,只考虑高阶振型本身的响应贡献,而不需要考虑振型间的耦联。既然如此,我们面对的问题是:为什么结构在弹塑性阶段,结构的高阶振型对结构的变形模式影响如此之大呢?笔者的理解是,结构在弹性阶段,亦存在高阶振型的影响,但是之所以不那么显著是因为在弹性阶段,结构因弹性刚度较大,其整体变形很小,所以显式不出来。但是一旦结构进入弹塑性阶段,结构的变形可以发展至弹性阶段变形的数倍甚至数十倍,那么在很大的变形基数下,这种高阶振型的对结构层间变形不均匀性的影响就会暴露出来。以一个两自由度为例。我们做一个假定,两自由度体系,分别在第一第二阶振型对应的力向量peff,n(t)(n=1,2)下,同时达到弹塑性位移的峰值。结构的整体响应即为两者的叠加。可知,该两自由度体系的顶层在二阶振型影响下,位移会进一步加大,而底层的位移则会会进一步减少,那么底层和二层的层间位移角就不再均匀,介于一阶振型和二阶振型之间。当然这是个特殊的情况,实际结构的响应更较为复杂,如一阶振型和二阶振型不一定同时达到正向峰值,这里不做过多讨论,仅仅给大家理解高阶振型对变形模式不利影响的一些显式的理解。总结一下,结构的高阶振型对结构的变形模式的影响存在于结构受力的各个阶段,只是结构在弹塑性状态下,结构利用其变形能力来达到耗能并降低地震响应,因而位移响应较大,所以高阶振型在此阶段下影响被放大出来。这一点结论也和当下的关于旗帜型自复位结构由于耗能不足,结构峰值响应更大,高阶振型的影响较传统结构更为显著的结论相呼应。

写在最后
既然了解了高阶振型产生的机理,那么我们在结构设计中可以通过哪些方法降低高阶整形的影响呢。这里为了和前文衔接,我们仅从理论上探索可行的方式,不在结构形式上做文章,因为时下对结构整体变形可控的结构整体构造方法也有很多学者研究,比如配备摇摆墙,强行使得结构变形呈现出基本模态。理论上,我们发现,降低结构的峰值响应,结构的高阶振型的不利影响就会显著降低,比如若结构始终弹性阶段,且不考虑层间加速度对非结构构件的影响,以及住户的舒适度,那么高阶振型的不利影响几乎可以忽略。因为结构的整体变形很小。所以对降低峰值响应的措施就是降低高阶振型的策略。已有的研究的表明,对于dual system( 拥有较高屈服后刚度系数的结构)可以显著降低结构的峰值响应,以及提高结构的耗能能力也是有效的手段。写到这,剩下的理论串烧就交给读者了。
最后投身抗震的小伙伴们加油哈!!




