Abaqus|如何模拟地震、噪音、颠簸路面激励下的不确定性振动行为？

在自然界，存在一些振源，无法用具体的时间和坐标函数来描述它，如地震、飞机起飞和降落过程、路面行驶汽车的颠簸过程等。随机振动分析的结果是统计学上的意义，是描述该现象在不同分位数（  1sigma,2sigma,3sigma）下发生的概率，得到的是标准方差下的位移、应力等。在Abaqus中随机振动分析的输入是通过功率谱密度（PSD）来定义的，有速度谱、加速度谱和位移谱。Abaqus将随机振动分析分为模态分析和随机振动分析两个分析步。

      针对如下图所示连杆结构，小孔固定，大孔右上端放置一质量为1kg的物体，模拟在随机振动下的连杆响应。

图1 带质量块的连杆机构

Abaqus分析步骤：

1.建立模态分析步；

2.建立随机振动分析步。

Property模块：

材料属性以及质量块的添加：在Property模块下进入SpecialàinertiaàPoint Mass/Inertia设置质量为0.001t（mm制单位），如图2所示。

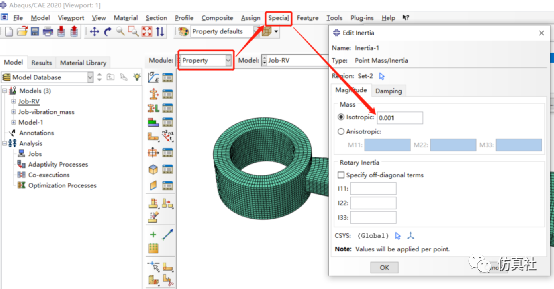
图2 质量快的定义

Step模块：

分析步1：模态分析步中的模型阶数设置为10阶。

分析步2：建立随机振动分析步如下，其扫频范围设置为20到1000，number of points为20,Bias等于3，意为每相邻模态的20个采样点集中在概率分布的一端，阻尼为0.05。

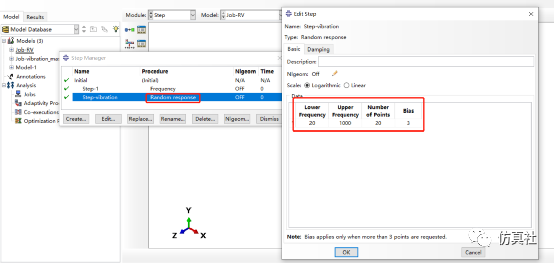
图3 定义分析步

因为随机振动分析的结果是标准差位移和应力，因此我们在Step中勾选RMISE和RU。此外分析结果中我们将监控RP-2的位移，因此为RP-2设置历史输出。

图4 参考点位置

Load模块：

设置RP-1固定约束。模型设加速度功率谱曲线如图5所示，在Abaqus中的设置如图6所示。

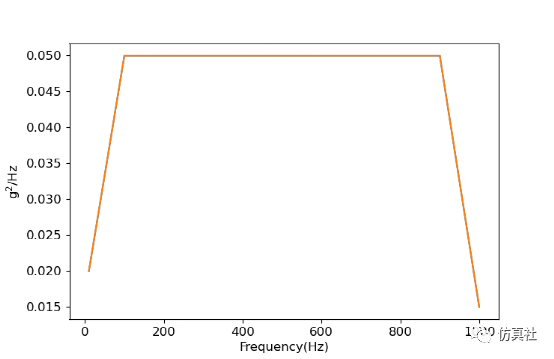
图5 加速度功率谱曲线

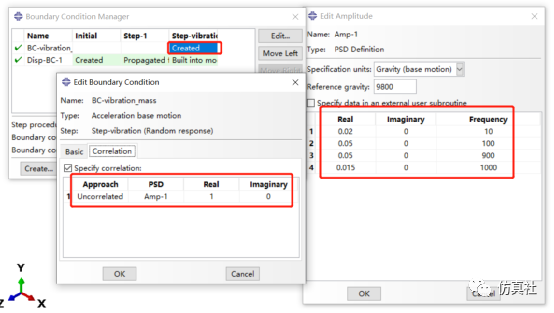
图6 加速度功率谱的定义

图7为连杆在随机振动分析中的模态振型图。由图8-图9，假设使用1sigma准则，则结构在此载荷下发生最大应力89.2MPa，最大位移为1.313mm的概率查表可知为0.6827。图10表明位移在频率为41时，其位移达到了稳定状态。

图7 不同模态下的位移振型

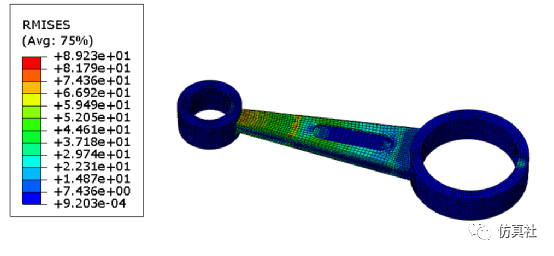
图8 RMISES云图

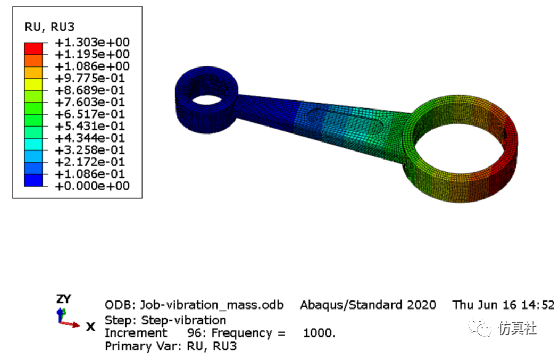
图9 RU3位移

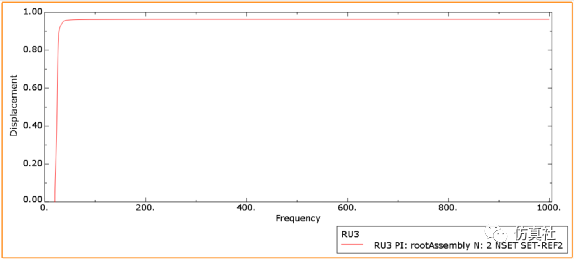
图10 RP-2的平方根位移误差