非线性有限元分析之超弹模型Ogden
本文摘要(由AI生成):
本文介绍了Ogden模型在超弹性材料中的应用,包括其数学和实验基础,以及与其他超弹模型的比较。Ogden模型以主伸长率为自变量,直接表达应变能函数,适用于大应变和非定常剪切模量的材料行为模拟。文章还介绍了Ogden模型的优点和限制,以及含有三阶Ogden材料模型的有限元分析实例。虽然应变能函数的形式选择不太重要,但模型的选择应根据系数拟合的难易程度和非线性收敛效率来决定。
在以前的文章中,我们已经分别介绍了 Arruda-Boyce, neo-Hookean,Mooney-Rivlin,Yeoh,Gent, Blatz-Ko等几种常用于非线性有限元分析的超弹模型。今天要介绍一个特殊且广泛适用的超弹模型:Ogden。一个非常通用,可以用于橡胶,大分子材料,和生物组织的超弹模型。Ogden模型已经被成功地应用于O 形圈、密封圈和其他工业产品的分析。而它的最大特殊性在于理论算法上采用了主拉伸作为基准变量,而不是常见的应变张量不变量。和Mooney-Rivlin等其他超弹模型一样,Ogden是以人姓氏命名的超弹模型,用以感谢Ogden博士在此超弹模型上作出的贡献。

1972年,在英格兰东安吉拉大学(University of East Anglia)做研究员的Ogden博士,在著名的Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences期刊上,发表一篇名为Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubberlike Solids文章,长篇描述了Ogden模型,以及和其他超弹模型的数学与实验基础。全文条理清晰,行文流畅,读起来也令人赏心悦目。Ogden放弃了应变能函数是主伸长率的偶函数的假设,认为采用不变量来描写应变能函数是不必要的复杂化,他直接用伸长率作为自变量来表达应变能函数,并给出了实验和理论模型的对比。由于可压缩Ogden模型和不可压缩Ogden模型具有非常相似的特性,本文就只介绍不可压缩Ogden模型,可压缩模型会在以后的文章中加以介绍。WELSIM已经支持了Ogden不可压缩模型。

1943年,Raymond William Ogden出生于还在经历二战的英国。1967-1970年在英国剑桥大学攻读博士学位,师从力学界著名的Rodney Hill教授,博士论文题为弹塑性材料的本构关系(On Constitutive Relations for Elastic and Plastic Materials)。1970年博士毕业后,在英格兰东安吉拉大学从事研究员工作。从1984年开始,Ogden在Glasgow大学的数学与统计学系任教授。学习非线性弹性力学的朋友们一定都有收藏他的经典名著Nonlinear Elastic Deformations吧。2006年Ogden入选英国皇家学会会士(Royal Society Follow)。和Rivlin,Gent等他的前辈们不同的是,这位英国出生的力学家并没有移 民美国,而是一直在英国的大学从事研究与教育工作。
Ogden模型的应变能势函数
Ogden模型的应变能势函数是基于左手柯西格林应变(left Cauchy-Green strain)张量的主伸长率(principal stretches)的,有如下形式:
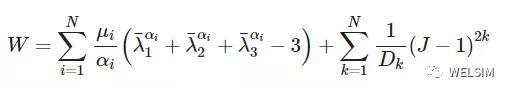
其中,N为模型的阶数,通常N取1-3之间的数。u_i和a_i为材料常数,其中u_i单位是压力,a_i是无纲量,无单位。D_i为不可压缩参数用于表示体积变化。缩减主伸长率具有如下关系
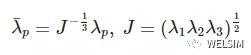
从此应变函数中我们可以知道:
模型以应变张量的三个方向上的主伸长率λ1、λ2和λ3为变量。
初始剪切模量为u=sum(u_i*a_i)/2。初始体积模量为K=2/D_1。
当N=1, a1=2时,转化为neo-Hookean模型。
当N=2, a1=2, a2=-2时,转化为2参数Mooney-Rivlin模型。
由于主伸长率是应变张量特征值的平方根,算法上需要计算3x3应变矩阵的特征值来获得材料刚度矩阵和应力。
输入材料常数需满足u_i*a_i>0,以保证算法稳定性。
Ogden模型的优点与限制
通用。可以广泛应用于各类型的超弹本构关系。在橡胶的整个应变范围内部具有较好的模拟能力。
适合处理大应变问题。当N=3或更高时,可达到所需要的精度要求。Ogden模型在应变高达700%时还能够很好的拟合试验数据。
适合描述非定常剪切模量和轻微压缩的材料行为。
能够描述应变后期刚度急剧上升的状态。
不同的实验类型所确定的材料参数无法用于其他变形工况模拟。在实验数据不足的情况下不建议使用,如只有单轴拉伸实验结果。
含有三阶Ogden材料模型的有限元分析
定义材料
选用Ogden 超弹材料,并输入参数u1=0.69 MPa, a1=1.3, u2=0.01 MPa, a2=4.0, u3=-0.0122, a3=-2, D1=0.1 MPa^-1,D2=0.1 MPa^-1,D3=0.1 MPa^-1。
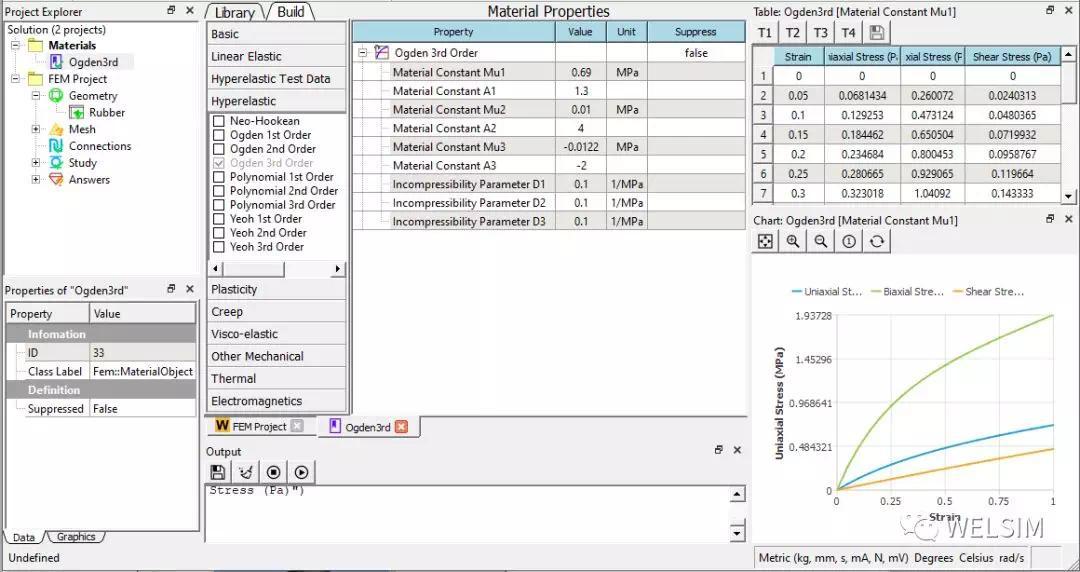
导入橡胶几何体,划分网格,并在侧面施加5e-3 MPa正压力。
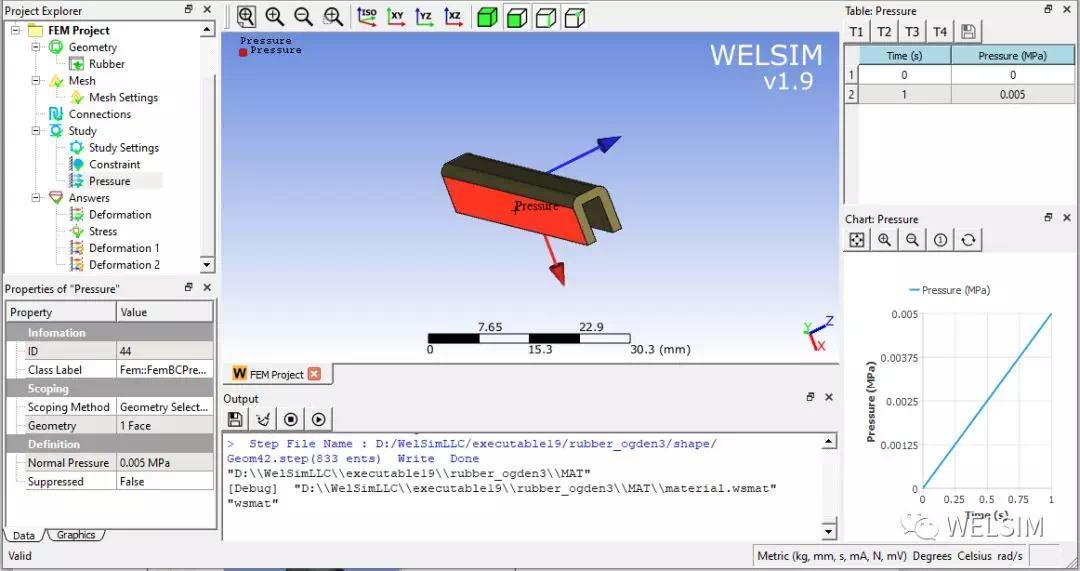
求解,并添加位移结果节点,显示云图和时间历程最大最小值。如图所示,Z方向变形随时间变化表现出非线性。
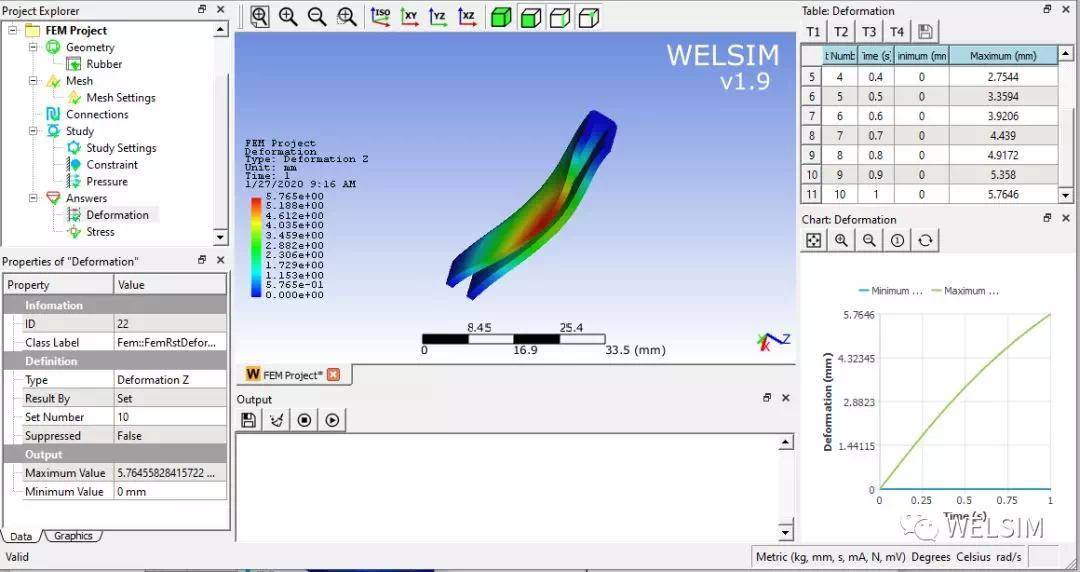
事实上,从实际有限元分析的角度出发,只要模型能用合理的拟合系数较精确地表达橡胶材料的力学特性,应变能函数不管用应变不变量还是主伸长率来表示都显得不那么重要。模型的选择,主要是根据系数拟合的难易程度以及非线性收敛效率来决定了。




