非线性有限元分析之超弹模型Blatz-Ko
本文摘要(由AI生成):
本文介绍了有限元分析中另一个具有特点的超弹模型——Blatz-Ko模型。该模型特别适用于描述可压缩大变形材料,如泡沫橡胶的力学性能。文章提到,Blatz-Ko模型由Paul J. Blatz教授和William Ko博士于1962年提出,并已得到广泛应用。该模型具有简洁、准确、有效的特点,适用于描述泡沫橡胶这类可压缩超弹材料的力学行为。文章还探讨了Blatz-Ko模型的优缺点,并展示了含有该模型的有限元分析过程。
有限元分析中常用的超弹模型如Arruda-Boyce, neo-Hookean,Mooney-Rivlin,Yeoh,和Gent我们都已经介绍过了。今天,我们来讨论另一个非常有特点的超弹模型:Blatz-Ko。如果说大多数超弹模型都主要适用于不可压缩材料的话,那Blatz-Ko则正好相反,它非常适合用于描述可压缩大变形材料,如泡沫橡胶的力学性能。也是应用最广泛的应用于泡沫橡胶的材料本构模型之一。Blatz-Ko是以两位人姓氏组合命名的超弹模型,用以感谢Blatz和Ko博士在此超弹模型上作出的贡献。

1962年,Paul J. Blatz教授和他来自台湾的博士生William Ko在Transactions of society of rheology期刊上发表了一篇名为Application of Finite Elastic Theory to the Deformation of Rubbery Materials的长篇文章,描述了Blatz-Ko模型及其实验依据。WELSIM也已经支持了Blatz-Ko超弹模型。为发泡聚氨酯橡胶这类可压缩超弹材料,提供了一个简洁,准确,有效的力学模型。这篇经典文章都是两位作者在加州理工(California Institute of Technology)工作和求学时所发表。来自台湾的Ko博士还有一个中文名叫柯威霖,加州理工毕业后一直在美国宇航局(NASA)从事研究工作。Ko的这篇文章也是华人在非线性力学及其有限元领域增加一份贡献。

一般将多孔橡胶或弹性泡沫材料统称为泡沫材料。弹性泡沫材料的普通例子有多孔聚合物,如海绵、包装材料等。泡沫橡胶能够满足非常大的弹性应变要求,拉伸时的应变可以达到500%或更大,压缩时的应变可以达到90%或更小。与固体橡胶的几乎不可压缩性相比,泡沫材料的多孔性则允许非常大的体积缩小变形,因此具有良好的能量吸收性。小应变 <5%,线弹性,泊松比为0.3 。大应变,压缩时,泊松比为0.0;拉伸时,泊松比大于0.0。这些特殊的力学特性,就很适合用Blatz-Ko模型来描述。
Blatz-Ko的应变势能函数有通用函数形式,而有限元方法中最常用的是其低阶形式。如下:
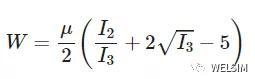
其中,u为初始剪切模量,I2和I3分别是第二和第三应变张量不变量。由于体积变化量和偏离量合在和一起,不再需要其他超弹模型的不可压缩参数。值得注意的是,这里的I2和I3为原始的应变张量不变量,而不是缩减不变量(reduced invariant)。从应变能函数表达式可以看出:
只有一个输入参数:初始剪切模量u。
初始体积模量为K=5u/3。体积相关的势能和体积无关势能是强耦合在一起。这点和其他超弹模型有本质不同。
Blatz-Ko模型的优缺点:
简单,参数少。只要输入1个参数。因此,所需要的实验量也少。
能够表现出泊松比数值较小下的材料力学行为。
和所有的低阶少参数模型一样,Blatz-Ko难以准确描述整个应变历程下的所有状态。
含有Blatz-Ko材料模型的有限元分析
定义材料
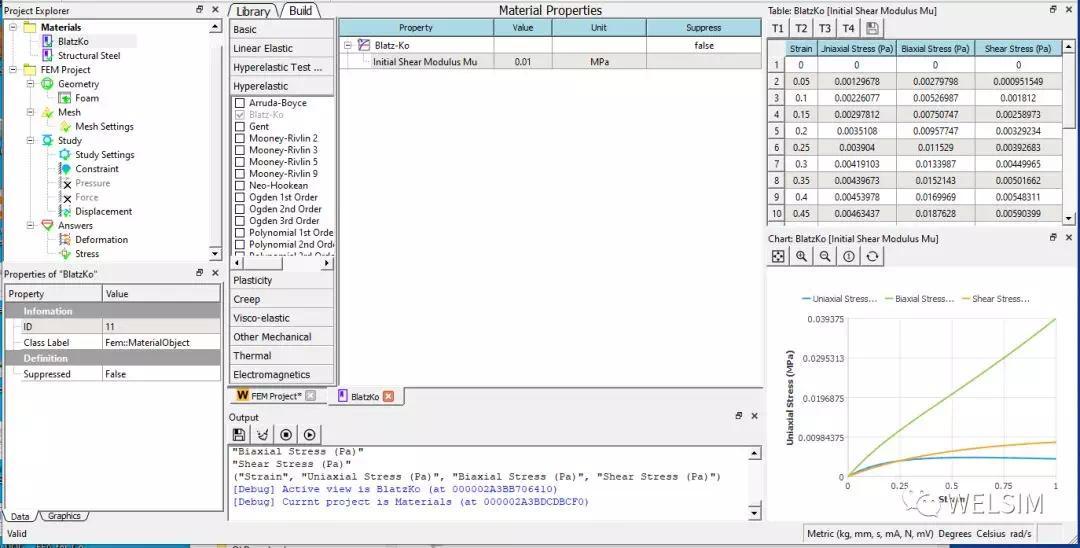
选用Blatz-Ko 超弹材料,并输入参数u=0.01 MPa。
导入橡胶几何体,划分网格,并施加向下压缩的-7mm的位移

求解,并添加应力结果节点,显示云图和时间历程最大最小值。如图所示,最大应力值随时间变化表现出非线性。