非线性有限元分析之超弹模型Yeoh
本文摘要(由AI生成):
本文介绍了Yeoh超弹模型,它是一种以人的姓氏命名的经典超弹模型,用以描述橡胶等材料的非线性弹性行为。该模型由Oon Hock Yeoh提出,并通过加入一个含有指数衰减的项来描述炭黑填充橡胶在小应变下的剪切模量减小现象。Yeoh模型具有简单、参数少、可描述变形范围宽、能够体现反S型应力-应变曲线等优点,但也存在预测等双轴拉伸时偏差较大、处理复杂综合应变时偏差较大等缺点。在实际应用中,推荐使用N=3的3阶版本。通过有限元分析,可以模拟橡胶结构的应力分布和变形情况,并验证Yeoh模型的适用性和准确性。
前几篇文章中,我们分别介绍了 Arruda-Boyce, neo-Hookean,和Mooney-Rivlin几种经典的超弹模型。今天,我们来聊一聊Yeoh超弹模型,也称作缩减多项式(Reduced Polynomial)模型。这也是以人的姓氏命名的超弹模型,用以感谢Oon Hock Yeoh在此橡胶超弹模型上作出的贡献。
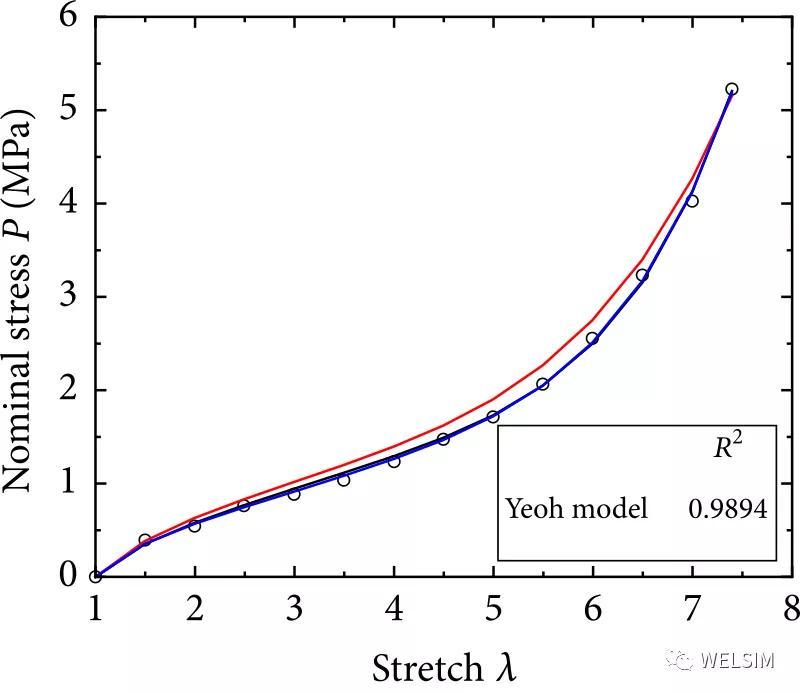
1990年Yeoh发现炭黑填充橡胶即使在小应变状况下,剪切模量会发生显著的减小。1993年,Yeoh发现即使没有没有炭黑填充的橡胶,也会具有这种现象。然后他通过加入一个含有指数衰减的项,来描述此现象。并在Rubber Chemistry and technology发表了一篇名为Some forms of the strain energy function for rubber的论文来描述了这个理论。WELSIM已经支持了Yeoh非线性模型。

关于Oon Hock Yeoh本人的信息很少,只能从姓氏知道是一位马来西亚华人,姓氏对应的中文的是“姚”。算是有限元体系中为数不多含有华人元素的理论吧。Yeoh现在是美国Freudenberg-NOK密封科技公司的会士员工,曾经在马来西亚橡胶研究所(RRIM),Akron大学, 美国GenCorp研究所,美国Lord公司工作过。和Mooney与Rivlin等物理学家一样,都是工业界中,从事橡胶研究的力学家。
和其他超弹模型一样,我们用弹性应变能函数来描述此模型。Yeoh模型的弹性应变能函数为:

其中,J是变形后与变形前的体积比,对不可压缩材料,J=1。I1是第一应变张量不变量。N, Ci0和Di为输入参数。从应变能函数可以看出:
Yeoh和Mooney-Rivlin非常类似,同属于多项式(Polynomial)形式家族。同样阶数下,由于不考虑第二张量不变量I2的作用,Yeoh要比Mooney-Rivlin形式上要简单许多,只是在含有不可压缩参数D的项会存在高阶的复杂性。
初始剪切模量为2*C10,初始模量为2/D1。为了保证初始剪切模量为正值,参数C10必须大于0。
虽然阶数参数N可以很大,但实际应用中,我们至多只用到3阶。由于当N=1时,等同于neo-Hookean模型。所以一般推荐使用N=3的3阶版本,以此体现出Yeoh模型的优越性。
N>=3时可以描述典型的反S形橡胶应力-应变曲线。
Yeoh优点
简单,参数少。用户只需很少的实验数据就可得到合理的数值结果,输入参数可以仅通过拉伸数据获得。
可描述的变形范围较宽,在很大的单轴拉伸和简单剪切变形可得到合理的结果。
高阶形式能够体现反S型应力-应变曲线,能模拟应变后期材料刚度急剧上升特点。高阶版本可以描述炭黑填充橡胶的变剪切模量的特性。
Yeoh缺点
在预测等双轴拉伸的应力-应变关系时,表现出一些偏差。
在处理复杂综合应变时,会有较大偏差。
对于小应变工况,需要谨慎选择参数。在小应变区,Yeoh模型和实验数据会存在偏差,但对于有限元分析中这点偏差并不严重,因为在小应变区应力很小,尽管相对误差可能很大,但是绝对误差很小。
Yeoh模型的非线性有限元分析
选用Yeoh 3 超弹材料,并输入炭黑填充橡胶的参数C10=0.57382 MPa, C20=-7.4744e-2 MPa, C30=1.1321e-2 MPa, D1=0.01 MPa^-1, D2=0.1 MPa^-1, D3=0.5 MPa^-1.
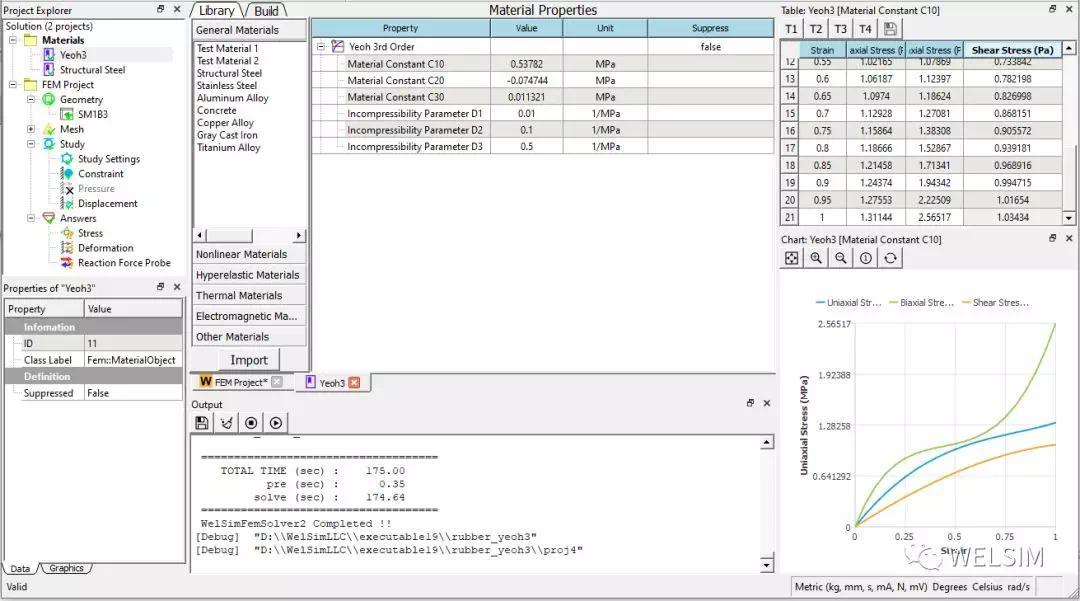
导入橡胶几何体,划分网格,约束底部,并在顶端施加向上拉伸100mm的位移

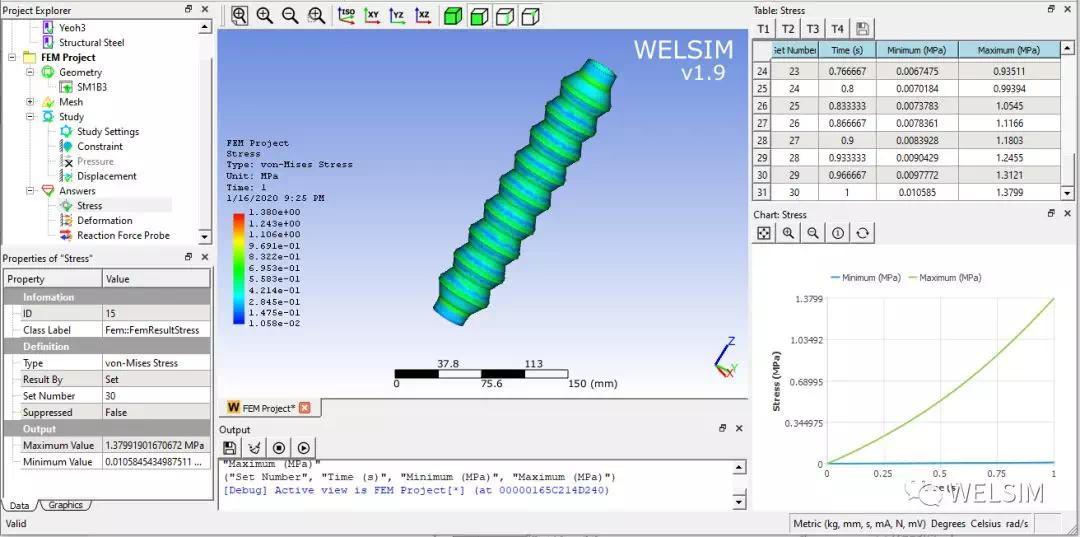
求解并加入结果节点,显示应力云图和时间历程下最大最小值。应力最大值曲线体现出非线性。
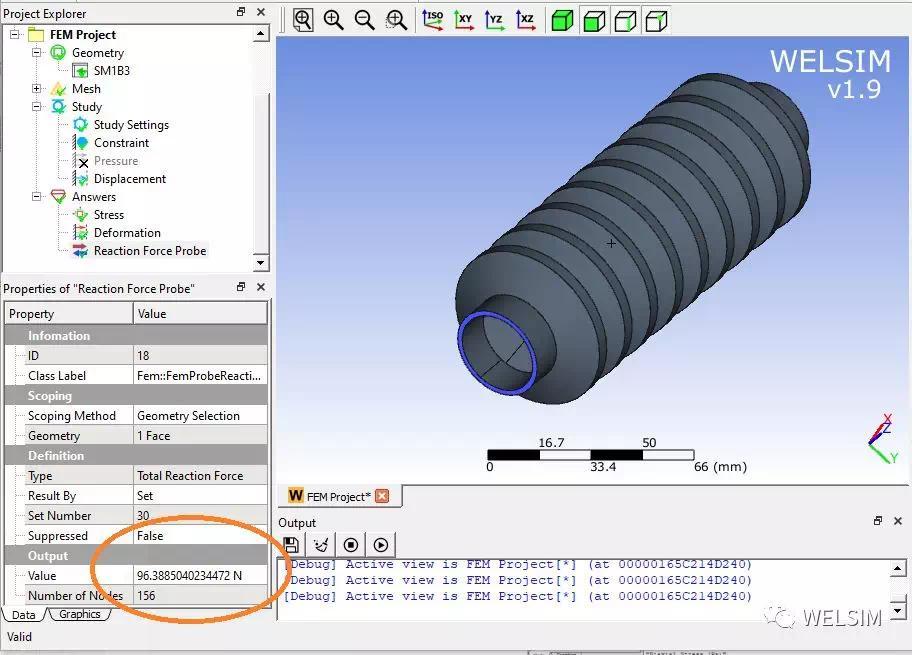
橡胶结构底部的反作用力为96.39N。