曲面调和映射的乌伦贝克定理
【这世界需要的不是反复倒伏的芦苇、旗帜和鹅毛,而是一种从最深的根基中长出来的东西。真东西。应该向上生长出来。 - 海子 】
2019年3月19日,由丘成桐先生推荐,美国数学家卡伦·乌伦贝克教授,获得了阿贝尔奖。今年是这一奖项首次出现女性得主。在给乌伦贝克的推荐信中,丘先生写道:“乌伦贝克教授是我们这个时代最杰出的数学家之一。她在极小曲面、调和映射、杨·密尔斯理论、非线性波和可积系统方面做了开创性的工作,这些在过去40年里塑造了几何分析领域。她的工作对微分几何、偏微分方程、拓扑和数学物理都产生了巨大的影响。”
多年之前,丘先生就给老顾讲过乌伦贝克的奇闻轶事:有一次,乌伦贝克和丘先生合作研究Kähler流形上Hermitian-Yang-Mills方程,在关键环节上遭遇困难。乌伦贝克将自己反锁在室内,整整一周足不出户,废寝忘食,将其一举攻克。乌伦贝克教授顽强的斗志,昂扬的激情,深厚的功力都令人叹为观止。
这里,我们简单介绍一下曲面调和映射的几何分析方法。众所周知,丘先生追随陈省身先生学习微分几何,同时和Morrey教授学习偏微分方程,然后将这两大领域相结合,创立了几何分析学派。调和映射理论完美地体现了几何分析方法的特点,既依赖于微分几何的理论,又用到偏微分方程的手法。曲面的调和映射理论更加丰富,除了需要用到微分几何和偏微分方程,也需要用到代数拓扑和共形几何理论。
半壁江山
在计算机视觉、医学图像等领域比较不同的几何形体具有根本的重要性。例如在医学图像中,病患的组织器官被拍摄下来,得到CT断层扫描或者核磁共振图像,有时候器官表面被抽取重建起来,然后和健康的器官进行精确的定量比较,从而帮助医生进行诊断。 例如通过比较大脑皮层曲面,判断阿兹海默症;比较膀胱内壁,诊治膀胱肿瘤等等。这些都归结为求取几何曲面(或者实体)之间的光滑双射(微分同胚),并且尽量减小几何畸变,这被称为是曲面(实体)配准问题。

图1. 比较大脑皮层曲面判断阿兹海默症。

图2. 比较膀胱内壁,判断膀胱癌症。
在医学图像领域,有两种比较常见的曲面配准方法,LDDMM算法和调和映射算法。LDDMM算法大致思路如下:假设源曲面和目标曲面都嵌入在三维欧氏空间中的单位立方体内,我们计算一族单位立方体到自身的微分同胚,这族微分自同胚将源曲面同伦(同痕)变换成目标曲面。微分自同胚族由单位立方体中的时变光滑矢量场所决定,光滑矢量场的计算归结为一个变分问题。这种方法为了计算二维曲面间的微分同胚,实际计算了三维立方体之间同痕变换,计算量较大;同时,如果源曲面和目标曲面彼此拓扑等价,但是并不同痕等价(即存在同伦变换,并且每一步都是嵌入),LDDMM方法无法得到微分同胚。相反的,调和映射方法只在二维曲面上进行计算,同时保证几何畸变最小;更进一步,调和映射方法是内蕴的,只需要黎曼度量信息,对于拓扑同胚、但是非同痕等价曲面也可以算出微分同胚。
目前医学图像领域调和映射方法不似LDDMM方法普遍,一方面有LDDMM提出较早的历史原因,另一方面也有调和映射理论较为艰深的学术原因。但是,对于蓬勃发展的医学图像工业而言,调和映射方法高效新颖,完备高效,会有异军突起的潜力。可以大胆预言,调和映射方法将挑起医学图像领域几何配准算法的半壁江山。

图3. 动态人脸表情捕捉。
计算机视觉领域中三维人脸识别,动漫动画工业中动态表情捕捉也依赖于曲面之间的微分同胚,最终归结为曲面之间的调和映射。在工程领域调和映射的算法被日益推广,调和映射的理论日益被重视起来。丘先生和乌伦贝克教授数十年前的工作为此奠定了坚实的基础。
调和映射的概念


长度能量极值者被称为是测地线,测地线的欧拉-拉格朗日方程为
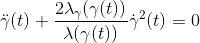

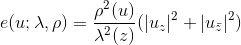




存在性
乌伦贝克给出了度量曲面之间调和映射的存在性证明。我们首先证明弱调和映射的存在性,然后再证明映射的光滑性;在证明过程中,我们先证明局部解的存在性,然后再推广到全局解。
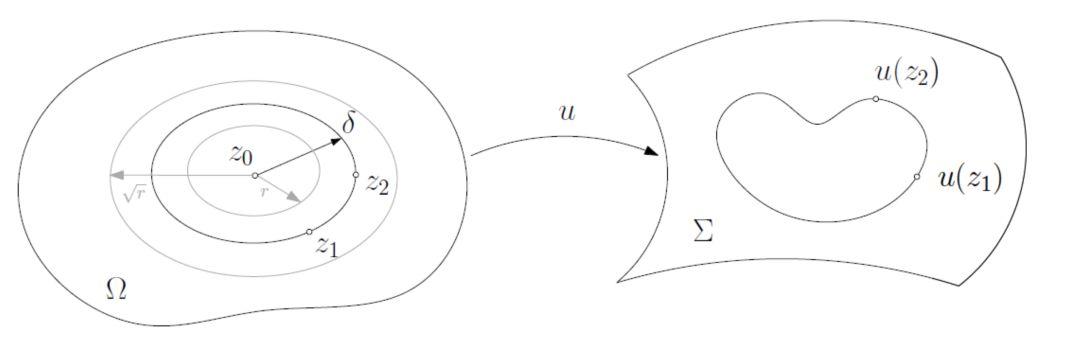
图4. Courant-Lebesgue引理



图5. 调和映射的最大值定理。

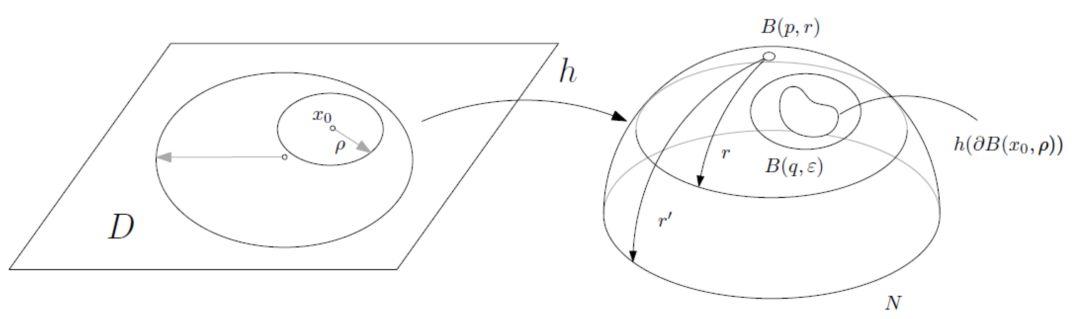
图6. Dirichlet定理。

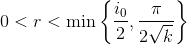

正则性


唯一性

这里,我们假设目标曲面处处具有严格负曲率。如果目标曲面曲率时正时负,那么有可能同一同伦类中,调和映射不唯一。
微分同胚性质
在度量曲面上成立Bochner公式,首先我们定义辅助函数:

这一公式可以用于证明曲面间调和映射的拓扑约束:
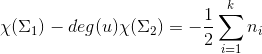
即曲面的欧拉示性数、曲面调和映射度和H零点阶之和满足的关系。辅助函数之差给出了映射的雅可比矩阵的行列式(Jacobian),

如果目标曲率非正,存在区域B使得上式为负,我们得到下调和函数(subharmonic function):


由此我们可以证明:如果源曲面和目标曲面是亏格相同的紧黎曼面,目标曲面上高斯曲率非正,拓扑度为一的调和映射必为微分同胚。
共形映射

曲面间的映射是调和的,当且仅当其对应的Hopf微分为全纯二次微分;曲面间的映射是共形的,当且仅当其对应的Hopf微分为0。

图3. 曲面调和映射的计算实例。
由经典的黎曼-罗赫定理,亏格为g的紧黎曼面上的所有全纯二次微分构成一个线性空间:亏格为0时,全纯二次微分空间维度为0;亏格为1时,此空间维数为复1维;亏格大于1时,此空间维数维复的3g-3维。
由此,亏格为0的紧黎曼面之间的调和映射必为共形映射。图3显示了一个拓扑球面到单位球面的调和映射,也是共形映射。
工程实现
从应用角度而言,调和映射理论在医学图像领域具有根本的重要性,目前由于其理论基础较为艰深,尚未普及。未来普及之后必会为增进人类健康做出杰出贡献。
从计算机实现方面而言,曲面由三角网格表示,用半边数据结构。调和映射算法是基于调和映射的均值定理:每一个顶点的像等于与这一顶点相邻的所有顶点的像的加权重心。加权平均算子在曲面的切空间中操作,曲面和切平面之间的变换由测地指数映射实现。同时,目标曲面的黎曼度量需要被更改为负曲率度量,这可以由离散曲面的黎奇流算法来实现。
感想
从理论角度讲,调和映射理论完美地体现了几何分析的手法特点:将微分几何和偏微分方程理论有机结合。曲面间调和映射的理论揭示了黎曼度量对于映射性质的本质决定作用,映射的正则性、唯一性和微分同胚性质都强烈依赖于高斯曲率;调和映射的存在性,和共形映射的区别取决于曲面的拓扑性质。这一理论将偏微分方程、代数拓扑和黎曼几何相结合,非常优美而富有诗意。
但是,人类社会的精细分工使得计算机工程师无法领略几何理论的深邃优美。在医学图像领域、计算机视觉领域,基于调和映射的工程论文汗牛充栋,但是绝不会有人引述乌伦贝克和丘先生的理论文章。大量的工程医学应用都是基于他们提出的理论,这些基础性的工作早已融入到现代文明之中。十数年来,老顾在世界各地讲学,深深体会到了老欧洲对于基础数学发自内心的尊重,也体会到美国文化的重商主义。
生平中,老顾遇到过很多计算机领域的博士,他们不满足于从工程角度出发的唯象直观解释,希望从更深的层次透彻理解算法背后的自然原理。有一次,老顾在清华讲解曲线测地流算法,一位计算机科学背景的博士生课后追问细节,很快老顾就发现他早就明瞭所有算法细节,实际上是在微分几何层面上穷根溯源。这需要索伯列夫空间的紧性和测地流方程演化中各种几何量的估计。他的思索超越了计算机科学的知识结构,但是周遭的环境对于他的深刻给与了冷嘲热讽,这令他迷茫落寞。曾经身边有过一位学生,在获得计算机博士学位的同时也得到优渥的工作岗位,但他却痛哭不已。他向老顾倾述,虽然得到了世俗意义上的成功,但他内心深知他所掌握的工程技能无法解答那些深刻的自然问题。他悲叹与童年梦想渐行渐远。
对于这些年轻人,老顾内心充满敬意。他们真诚面对自己的内心,没有盲从流行观点,没有畏惧探索真理的艰辛,对自然保持着纯真的好奇。从他们身上,老顾看到了人类文明发展的源动力。老顾也衷心希望,更多的年轻人能够志存高远,像丘成桐先生和乌伦贝克一样,凭借光辉的思想而留名青史!
1、Sacks, J. and K. Uhlenbeck, The Existence of Minimal Immesions of 2-Spheres, Ann. Math. 113 (1981), 1 -24
2、Schoen, R., and S. T. Yau, Existence of Incompressible Minimal
Surfaces and the Topology of Three Dimensional Manifolds
with Non-Negative Scalar Curvature, Ann. Math. 110 (1979),
127 -142
作者:【老顾谈几何】邀请国内国际著名纯粹数学家,应用数学家,理论物理学家和计算机科学家,讲授现代拓扑和几何的理论,算法和应用。
声明:首发老顾谈几何公众号(ID:conformalgeometry),部分图片源自网络,如有不当请联系我们,欢迎分享。




