浅谈牛顿迭代算法在ansys优化计算中的应用
本文摘要(由AI生成):
本文介绍了牛顿迭代算法的基本原理及其在软件中的实现。该算法用于求解方程的根,在仿真计算中具有重要作用。文章还通过一个具体的应用算例,验证了该算法在工程中的应用。算例采用workbench平台,利用IronPython语言实现牛顿迭代算法,对容器内气流混合过程进行计算。结果表明,该方法能够快速准确地找到满足要求的输入参数设计点,并达到设定的计算精度。与传统的直接优化和响应面优化方法相比,该方法在计算思路上有所不同,具有更高的效率和准确性。
牛顿迭代基本原理
根据牛顿迭代原理可知,设Xk是f(x)=0的一个近似根,把f(x)=0在Xk处作泰勒展开:
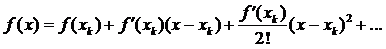
若取前两项来近似代替f(x) (称为f(x)的线性化),则得近似的线性方程
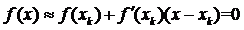
设 ,令其解为Xk+1,得
,令其解为Xk+1,得
这称为的牛顿迭代格式。当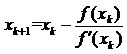 时,则认为找到了方程的解。牛顿迭代的一个重要特点是: Xk必须是所给区间f(x)=0的一个单根。
时,则认为找到了方程的解。牛顿迭代的一个重要特点是: Xk必须是所给区间f(x)=0的一个单根。
2.牛顿迭代的软件实现

图1 Step1算法流程图
在计算机仿真软件中,可以理解为,对某一个产品性能预期数值Yopt,期望求解对应的输入参数设计点Xopt。且对Yopt来将,对应的Xopt只有一个或不存在,即对不同的X值, Y值不同的。在workbench软件中,该算法主要是通过以下两个步骤实现的,其流程图如下图1和图2:

图2 step2算法流程图
3.应用算例
本文通过对workbench进行二次开发,在其平台上进行了一系列仿真计算,以验证本算法在工程中的应用。具体完成时通过workbench的脚本功能(Journal和Scripting)实现.在workbench中,脚本的编写是基于Ironpython实现的。
如图3所示,存在两个入口的一个混合管道,入口空气的速度和温度如图所示,左边入口进口速度为V1,温度为T1,右边入口速度也为V2,温度T2,下方出口速度为V3,温度为T2。假设左侧入口温度T1可调,但出口温度要求恒定为T3=324.8K.并设定左进口速度为V1=2.3m/s,右进口速度为V2=8.5m/s,,温度为T2=283K。计算精度要求在0.1K之内。求此时左侧入口的温度,空气物性采用理想介质。
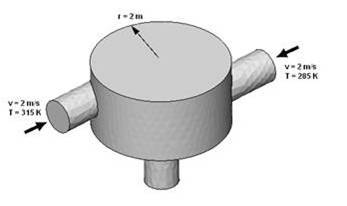
图3 计算模型
采用Workbench帮助文档自带的网格进行计算,并定义进口速度边界条件(给定初速度和温度),出口给定无回流的边界条件,残差设定为10^-4。将进出口条件参数化,并引入整个仿真计算中所需的各种物理量(K,flag,s,N,X0,X1,Y0,Y1,Yopt,Xopt,X2)。在Workbench的参数化模块(Parameter Set)中进行设置如图4所示。

图4 Parameter set示意图
通过分析可知,右侧入口温度为T2=283K,要求出口温度为T3=324.8K,则左侧温度大于324.8K。所以,给定X0=325,X1=1000,且满足s=0.1。
运行workbench上编写的相关二次开发程序可得,当左侧进口温度满足T1=669.1K时,出口温度满足要求。此时k=6,即进行牛顿迭代的次数为6次,也就是说整个计算只需要进行6次便达到了计算要求(计算精度)。可见,通过该方法,能够较为快速的实现由确定的输出计算结果得到相应的输入参数设计点。而且还可以获得确定精度的计算结果。
4.讨论
在workbench平台上,本文提出了一种基于IronPython语言的牛顿迭代算法,以实现仿真计算过程中“逆向”“闭环”“寻根”。最后,并以某容器内气流混合过程为例,具体实施了计算,验证了该算法的可行性和实际效果。
无论是DX中的直接优化(Direct Optimization)还是响应面优化(Response Surface Optimization),其本质都是要建立一个输入变量的样本空间,然后在选定的输入参数空间上实现计算以及进一步的拟合计算。可见,这种方法与本文提到的方法从计算思路上是有很大不同的。
根据ansys帮助文档可知,对于采用中心复合设计(CCD)方式的DOE实验,其设计点的数量是输入变量的函数,即
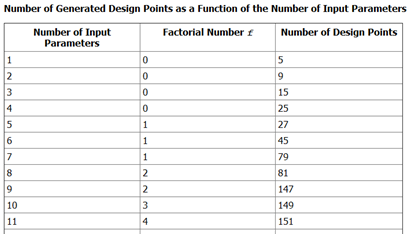
图4 workbench DX基于CCD方法的DOE设计点数量表
从上表可以知道,对于只有一个输入变量的情况,其设计点的数量为5个,如果这5个设计点对应的输出变量达不到设定标准,则只能采用拟合的方式,但拟合计算的准确度却是很难控制的。
可见,采用本文的牛顿迭代的方法进行输入变量的计算,能够较为快速的实现由确定的输出计算结果得到相应的输入参数设计点。而且而已根据设定的计算精度要求,获得相应的结果。




