非线性有限元分析之超弹模型Arruda-Boyce
在结构有限元分析中,常常会遇到非金属材料,如橡胶、生物等材料。由于这些材料的力学性能和金属材料的力学性能有很大区别,如弹性,大变形,不可压缩等等。力学家们将描述这类材料的模型统归一类,并称之为超弹(Hyperelastic)模型。

这些超弹模型或材料都有显著的特征:
能承受大弹性(可恢复)变形,应变可达100-800%;
由于材料分子链的拉直引起变形, 所以在外加应力作用下, 体积变化很小。因此, 超弹体几乎是不可压缩的;
应力-应变关系呈现出高度的非线性;通常, 拉伸状态下, 材料先软化再硬化,而压缩时材料急剧硬化。
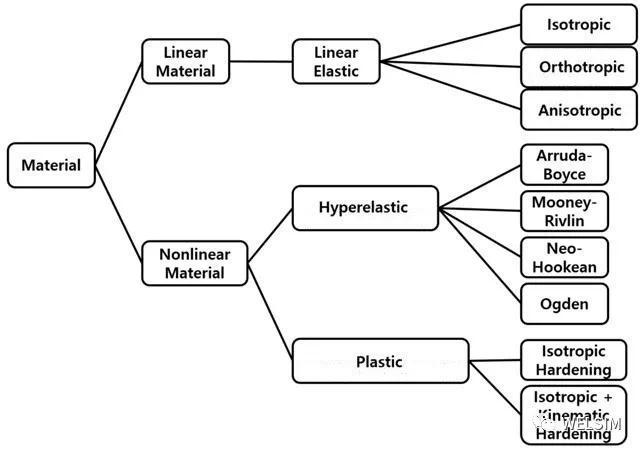
常见的超弹模型有:Neo-Hookean, Mooney-Rivlin, Odgen, Arruda-Boyce, Gent, Yeoh, Blatz-Ko等等。WELSIM也已经基本支持了这些模型。今天我们就来详细介绍一下 Arruda-Boyce。
1993年,MIT的Boyce教授和他的博士生Arruda在力学领域最知名的期刊之一 Journal of the Mechanics and Physics of Solids 共同发表了一篇名为A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials的文章,从而奠定了Arruda-Boyce模型的基础。

可见,相比较那些50-60年代的超弹模型,Arruda-Boyce还是比较新的。而且从文章的名字就可以看出,Arruda-Boyce在处理大拉伸时的表现更加灵活、准确。而文章发表27年后的今天,Arruda现在已是密歇根大学的正教授和机械工程系主任。Boyce是哥伦比亚大学的工程学院院长。值得注意的是这两位都是力学界少有的女性教授。
研究过超弹模型的小伙伴们都知道,我们都会用弹性应变能函数来描述一种超弹特征。Arruda-Boyce的弹性应变能的表达式为

其中
u 是初始剪切模量。
lambda 是有限网络的拉伸(limiting network stretch)。
D 是材料的不可压缩参数。当含有D的项为零时表示材料完全不可压缩。
J 是物体变形前后的体积比。
I_1 为Cauchy-Green张量的第一不变量。
Arruda-Boyce模型特点归纳如下:
默认为一种不可压缩的超弹模型。通过引入含有J的项引入可压缩属性。
当有限网络的拉伸参数无限大时,等同于Neo-Hookean模型。
有限网络的拉伸参数必须大于或等于1。
D1不能为零。
从超弹材料的分子结构模型中演化而来,采用8链分子结构为原型。因此对单轴拉伸和双轴拉伸都有很好的预测。
总体来说,Arruda-Boyce模型使用方便,一共只需要输入三个参数。且对大拉伸状况下的变形准确度高。对于具体参数的选用,需要根据材料的实验特性或手册等数据查找来确定。也可以通过测试数据的曲线拟合数值方法来确定参数。
非线性超弹材料分析实例
下面我们使用有限元软件WELSIM来模拟橡胶材料试件的拉伸试验,取全模型进行建模,在一侧位置施加位移,计算得到产生位移后的应力与反作用力状态。
分析步骤:
(1)设置单位制为英制,并创建结构静力学分析工程。
(2)设置材料属性。
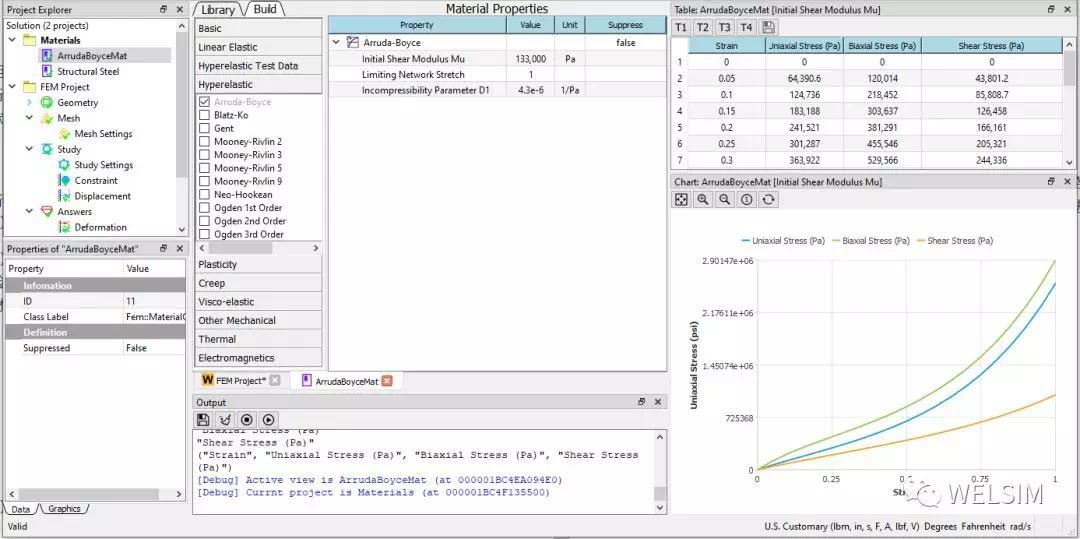
新建一个材料。双击此材料节点,进入编辑模式,从超弹材料属性中,加入Arruda Boyce属性。并分别赋值:Mu=1.33e5 Pa, lambda=1, D1=4.3e-6 1/Pa。定义完成后可以在曲线窗口看到对应模型的应力应变曲线。修改材料节点名称为ArrudaBoyceMat。
(3)建立模型。
新建一个块体(Box),并将尺寸设为 1x1x10 英寸。将上一步中定义好的ArrudaBoyce材料赋予这个几何体。
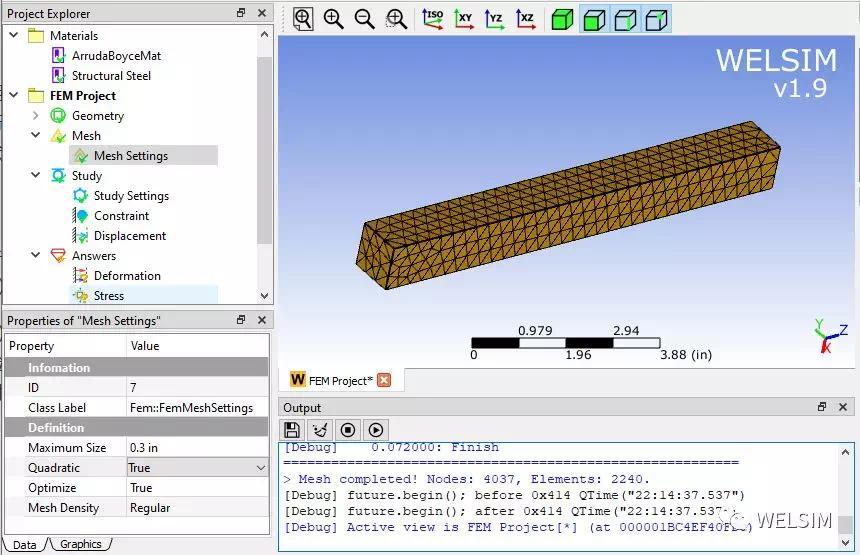
(4)划分网格:
设置最大单元尺寸为0.3英寸,并使用高阶的单元。网格划分后得到4037个节点,2240个Tet10单元。
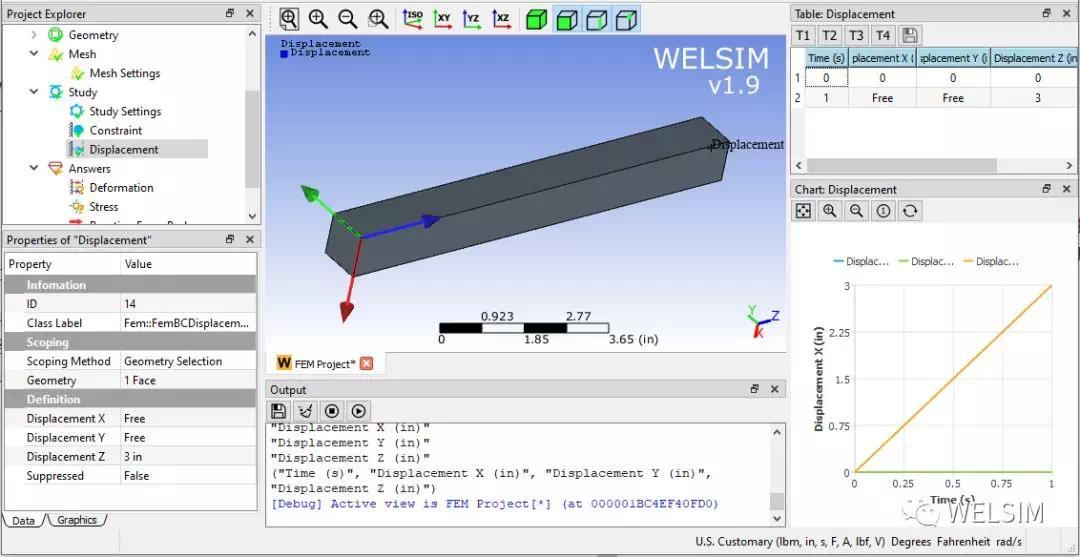
(5)施加约束及载荷
在左侧施加约束。
为了更好的体现Arruda-Boyce在大拉伸下的优势,在右侧端面设置Z方向3英寸的位移。
(6)求解设置,计算,及结果后处理。
为了便于收敛,我们设置10个子步。然后点击求解按钮进行计算。
查看等效应力(von-Mises stress)。
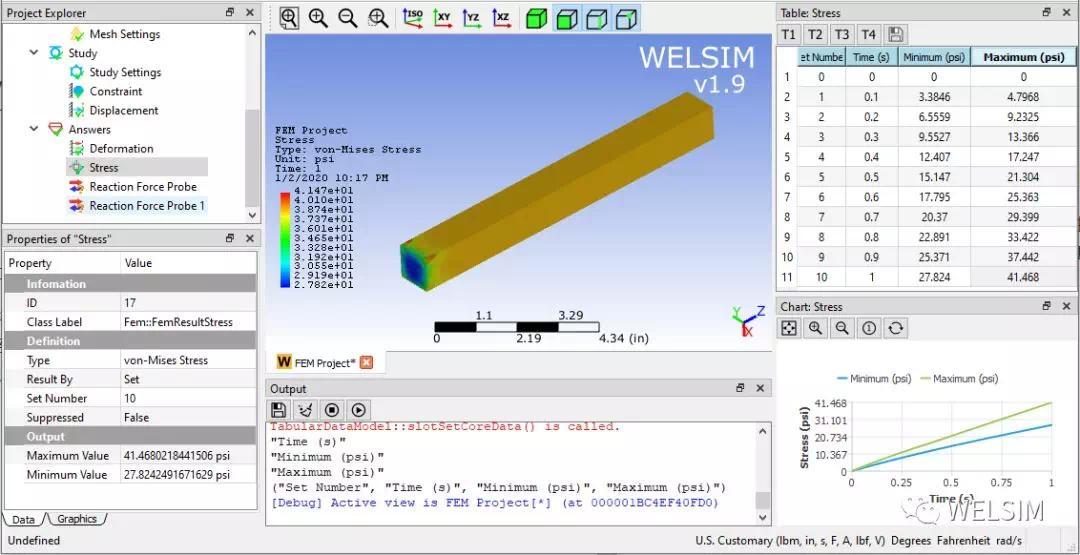
查看固定端的反作用力。和等效应力值吻合。
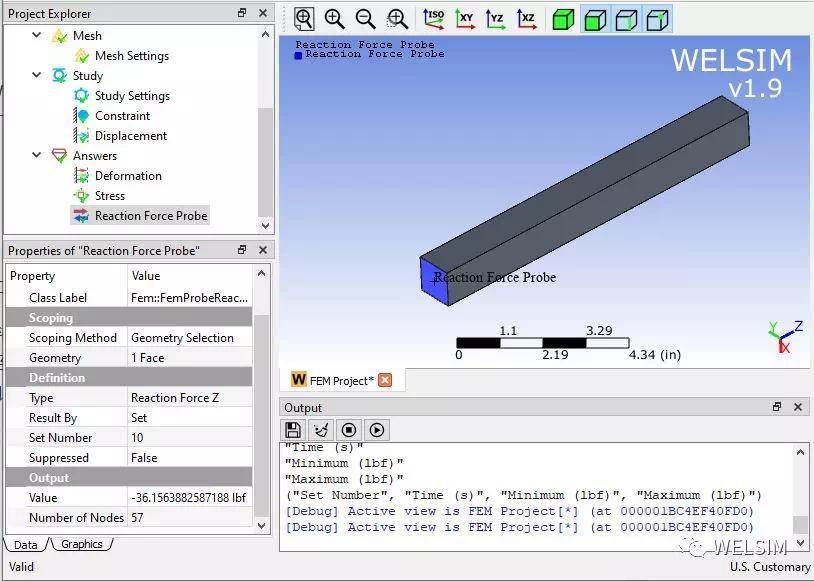
在有限元软件出现之前,材料非线性的计算与预测都比较复杂,手工计算超弹材料的应力与反作用,往往要花费很多的时间和工作。现在有了有限元软件,力学分析工作变得更快捷、准确、有趣了。





