多载荷步下的准静态(Quasi-Static)结构分析
本文摘要(由AI生成):
本文主要介绍了多步准静态分析的概念、计算机制和实例。多步准静态分析是一种快速便捷的变载荷分析方法,可以忽略惯性、阻尼和频率的影响,得到在不同外界条件下系统或结构的响应。在多步有限元分析中,常会遇到两个关于步的重要概念:步和子步。准静态分析的每个荷载步都是独立计算的,与前后荷载步均无关。在分析过程中,将整个加载过程分为若干个先后步骤,每个步骤可以分解为多个子步,保证每个子步收敛,最终实现每个步骤收敛。最后,文章以一个悬臂梁为例,展示了多步准线性分析的实例。
随着有限元分析技术的发展,工程师们已经不再满足于单步单载荷的静力分析了。为了更好地了解系统的结构动力学特性,我们会采用瞬态分析方法。瞬态有限元分析可直接计算输出结构动响应历程,但每个时间步输出一次全场应力和变形必然导致计算耗时长,结果文件过于庞大。因此,我们常常会对结构或系统进行多载荷步的稳态分析,又称准静态分析,以帮助我们快速了解系统及其对外力的响应。
多步准静态分析
尽管准静态在实际上并不存在,但作为一种基本力学模型,在工程实践上具有重要意义。很多实际问题可以近似归入准静态问题,并满足工程上的精度要求。准静态分析考虑了边界条件随时间变化的状况,可以得到在不同外界条件下系统或结构响应。尤其是对于包含有接触、碰撞、塑性、蠕变、膨胀、粘弹性材料等非线性问题,多步准稳态分析可以快速地得到近似结果。而对于那些系统惯性可以忽略不计的动力学问题,准静态分析的结果是可以直接用于工程实际的。

值得注意的是,准静态分析忽略了惯性、阻尼、和频率等影响。对于惯性无法忽略的系统或结构,准静态分析也为我们下一步进行全瞬态分析提供可靠的数值参考。
步的概念
在多步有限元分析中,常会遇到两个关于步的重要概念:
步(Step):通常指载荷步,在分析过程中,将整个加载过程分为若干个先后步骤;如分析弹塑性问题时,第一步加载,第二步卸载;当然加载过程也可以分解成多个Step,不过通常这个可以在求解过程中由多个子步(Substep)实现。
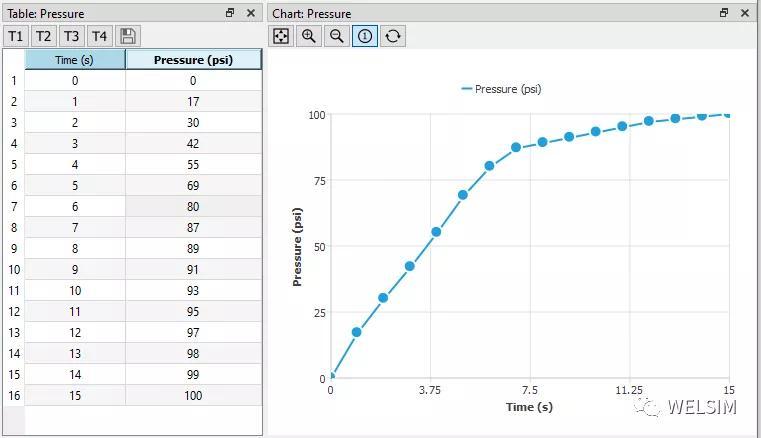
子步(Substep):如果每个载荷步(Step)是非线性的,为了求解,将其分解为多个Substep,保证每个Substep收敛,最终实现每个Step收敛。
多步准静态分析的计算机制
准静态的每个荷载步都是独立计算的,与前后荷载步均无关。虽然看上去后续荷载步是在前步的基础上计算的,然而每步计算是以结构的初始构形为基础。可以根据你本步的约束和荷载直接求解,而不用关心第一个荷载步。其结构对应的是你的约束和荷载情况,与前后荷载步均无关。
常见分析步骤
为了更好理解多载荷步,我们在有限元软件上来看一下如何设置多载荷步分析。本案例使用简单悬臂梁为例,外力随步数或时间变化。基本步骤为:
建立模型
划分有限元网格
设置载荷步数
设置多步边界条件
计算评价计算结果
可以发现,无论是线性分析或非线性分析,多载荷步和单载荷步的处理方式是一样的。区别只是在于载荷步数的设置,和边界条件对于每步的设置。
实例
下面我们以有限元软件WELSIM为例,来看一个多步准线性分析实例。
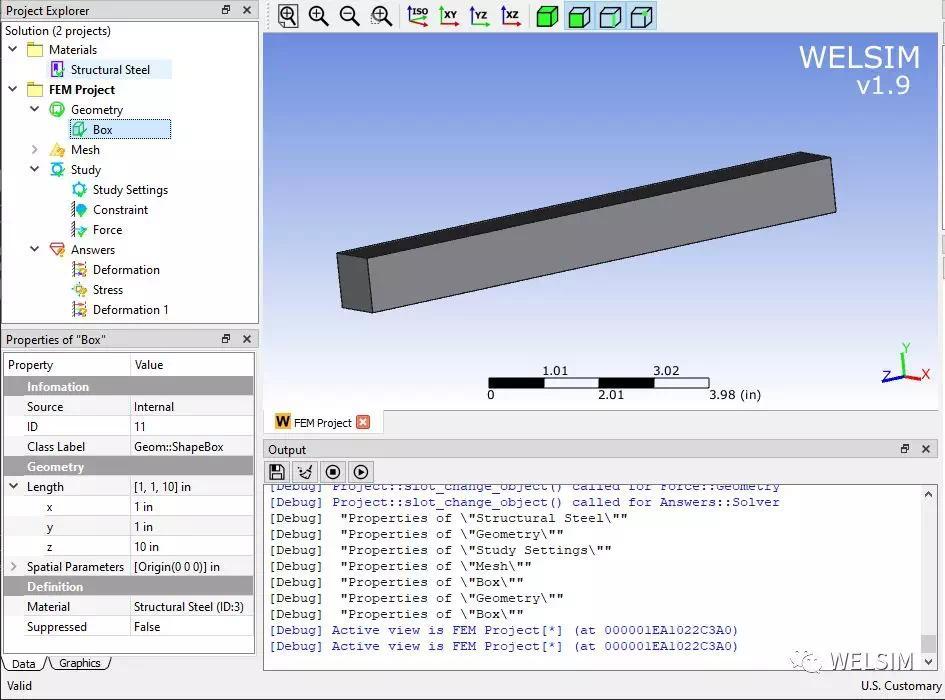
添加三维块状(Box)几何体,并设置长宽高分别为 1x1x10 英寸(in)。
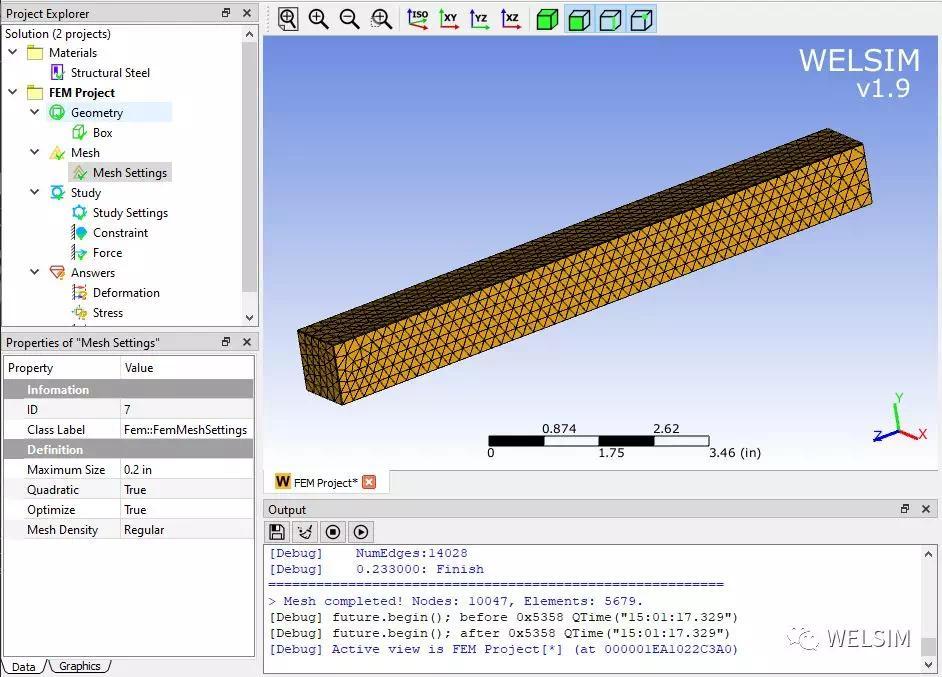
在网格设置中,设置最大单元尺寸为0.2 in,并按照高阶(Quadratic)网格划分Tet10单元。
多载荷步和单载荷步分析最大不同的就是载荷步数的不同。本例中我们设置3个载荷步。分析设置中,将载荷步数(Number of Steps)设置为3。双击分析设置(Study Settings)节点,可以看到弹出表格中显示了所有载荷步下的对应设置,其余保持默认。

梁的一端固定。
梁的另一端,由于是多载荷步,边界条件的属性窗口已经不能满足数值的输入。需要在表格窗口中,对应载荷步和纲量输入对应的值。这里在Y方向对应每个载荷步分别施加6000, -900, 6000 lb的力。其他方向力为零。
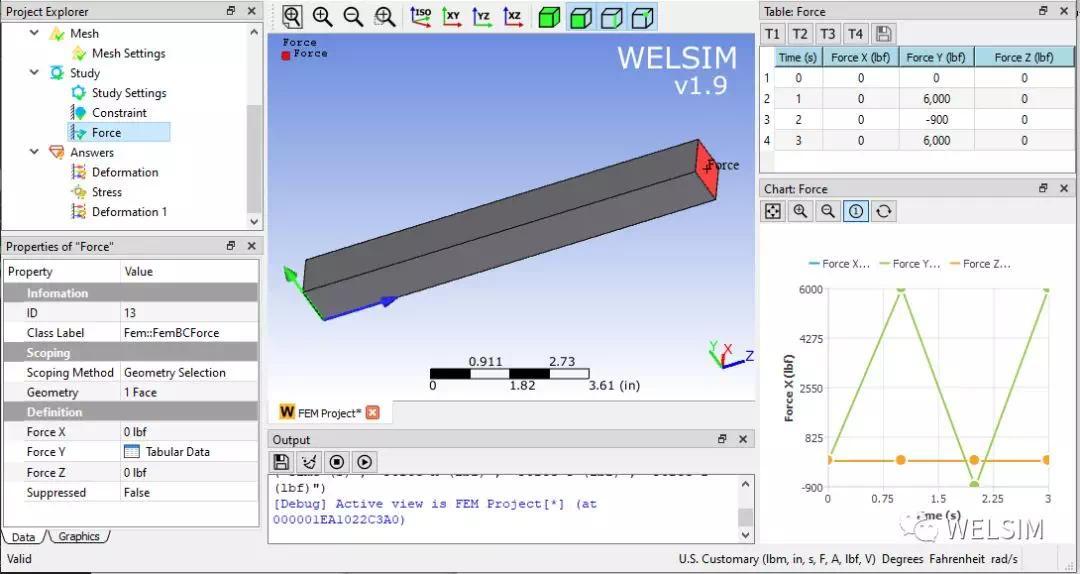
边界条件设置完成后,点击计算,很快就能得到结算结果。
第一个载荷步作用下,Y方向上的变形结果。

在第一个载荷步下的von-Misies应力结果。
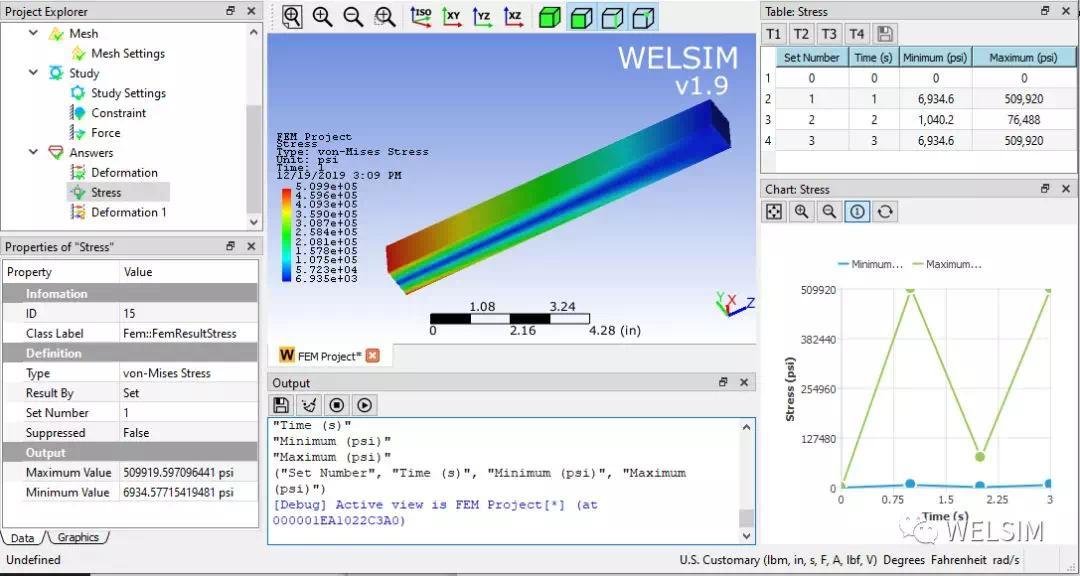
可以看到由于边界条件的变化,变形和应力也随之波动。第一载荷步和第三载荷步的结果一致,说明准静态忽略了惯性和频率的影响。但作为一种快速便捷的变载荷分析方法,多步准稳态分析还是具有很多实际工程作用的。





