各位读者看到的如下系列声学知识连载，是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique linéaire》（《线性声学基本现象》）的中文翻译。

11.3.4 板振动产生的声辐射

延长面为刚性面的板（Baffled plate）

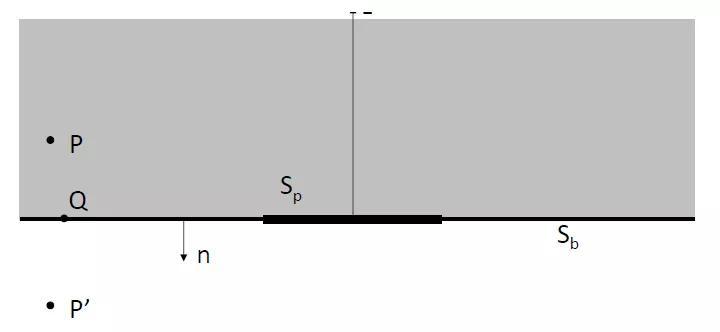
图11.16：延长面为刚性面的板（Baffled plate）

考虑一个外表面位移为u_z的板（图11.16）。这个板（plate）被插入到刚性平面（baffle）上。S_p和S_b分别表示板和刚性平面。我们想要计算在点P处的压力，同时定义与点P关于S_p∪S_b这个平面对称的点P′。Q是S_p∪S_b平面上的一点。现在我们将方程（11.54）应用到刚性平面上方的无界域V中：

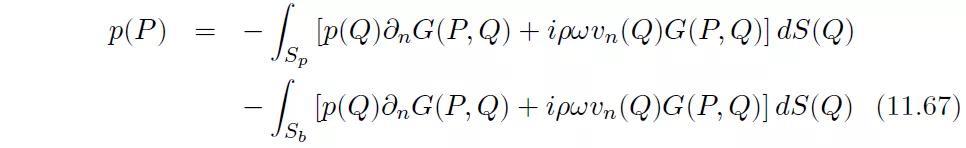
并且将方程（11.57）也应用到同样的无界域V中：

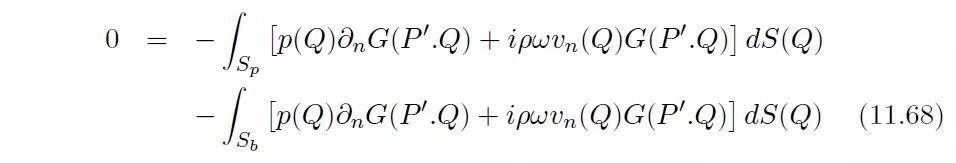
将上述两个式子相加，并考虑如下事实：

l  在S_b上有v_n=0;

l  在S_p上有v_n=－iωu_z;

l  在S_p∪S_b上有G(P,Q)=G(P^′,Q);

l  在S_p∪S_b上有∂_nG(P,Q)=-∂_nG(P',Q)=0;

则得到：

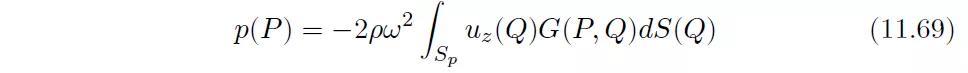
延长面为刚性面的活塞（Baffled piston）

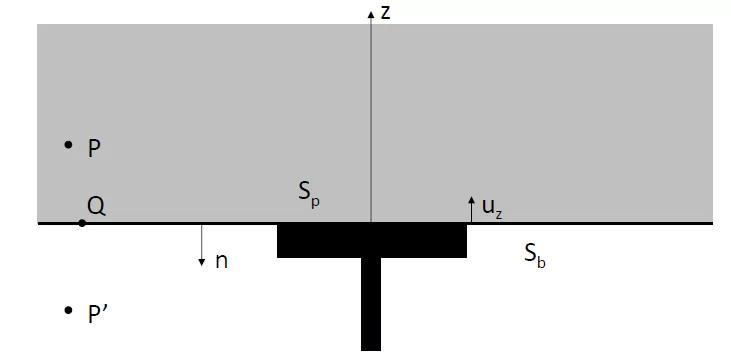
图11.17：延长面为刚性面的活塞（Baffled piston）

若考虑u_z是定值（振动平板转变为刚性运动的活塞），则由活塞辐射出的噪声如下：

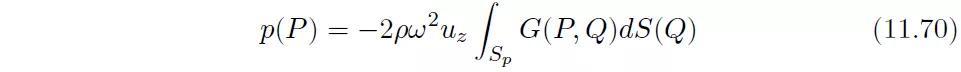
该积分可以用数值方法计算，也可以用解析方法计算。对于一个半径为10cm且具有1m/s²加速度（u=-1⁄ω² ）的圆形活塞的所产生的压力分布如图11.8 所示。如果活塞的直径相比于波长很小（即kr很小），则我们将上式积分视为常值，如下：

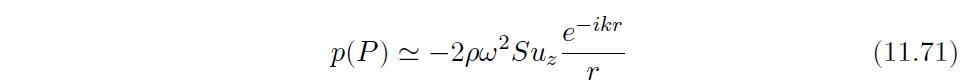
其中r为点P与活塞端面圆心之间的距离。在此种情况下，活塞所产生的声辐射场就如同单极子声源的一样。

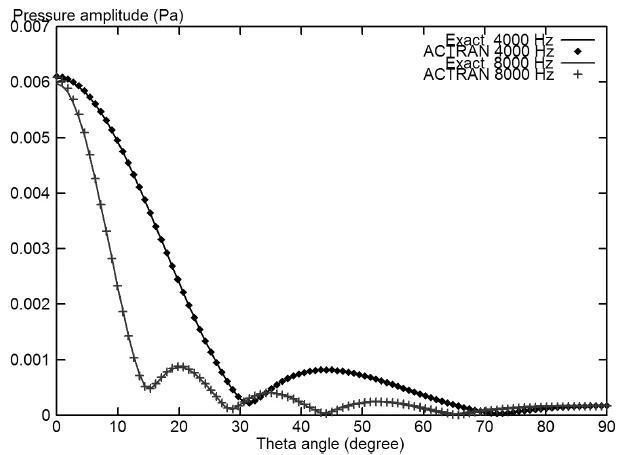
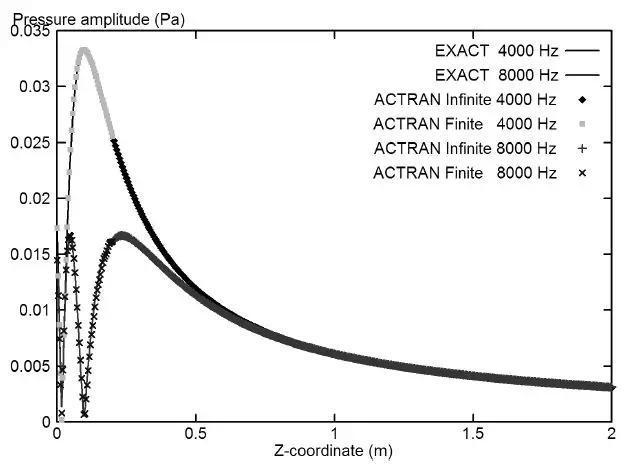
图11.18：具有挡板效应的活塞在4kHz及8kHz下的声辐射。上图：指向性图；下图：沿着活塞轴的压力分布

无刚性延长面的板（Unbaffled plate）

如果板没有刚性延长面，则可直接应用方程（11.66）：

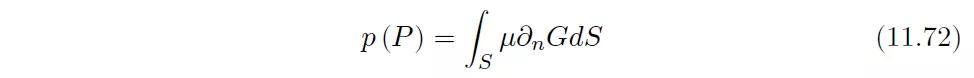
但是我们并不知道板两侧间的压力差μ。如果平板尺度与波长相比很小，我们还可以得到：

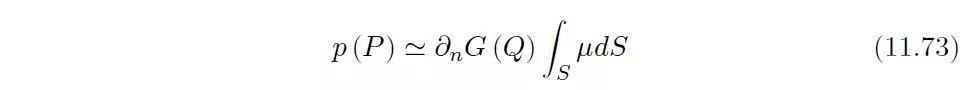
其中Q是板的中心。无刚性延长面的平板振动辐射声场的偶极子特性是很明显的，这点与有刚性延长面的平板振动辐射声的单极子特性相反。

11.4 声功率，辐射效率和阻抗（Power, efficiency and impedance）

11.4.1  辐射功率（Radiated power）

声辐射功率是有功声强（active intensity）在辐射表面或包含辐射表面的一个控制面上的积分:

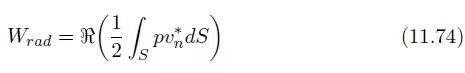
注意S可以被划分成几个部分（S=∪_i S_i）。那么，每一个子表面S_i都关联着一个声功率贡献量W_i。故总的声辐射功率可以表示成如下形式：

11.4.2  辐射效率（Radiation efficiency）

有时将声辐射功率W_rad与一传统使用的参考声功率W₀进行比较。该传统参考声功率在计算时认为辐射面S上的每一点均是独立辐射的，且均具有一个局部声阻抗ρc。

这两个辐射功率的比值就定义为辐射效率（radiation efficiency）：

11.4.3  辐射阻抗（Radiation impendence）

考虑一个管道（或任何声学组件），它通过一个开口面S_o连接到一个以无限刚性表面S_b为界的半无限空间（图11.19）。我们可以把式（11.69）应用开口面S_o上：

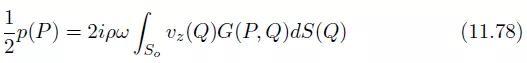
S_o上压力与速度分布的关系是非局域的。定义算子R为：

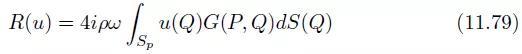
被称为半无限空间的辐射阻抗。压力与速度之间的非局域关系表示了在声学组件中半无限空间对声场的影响（图11.19）。

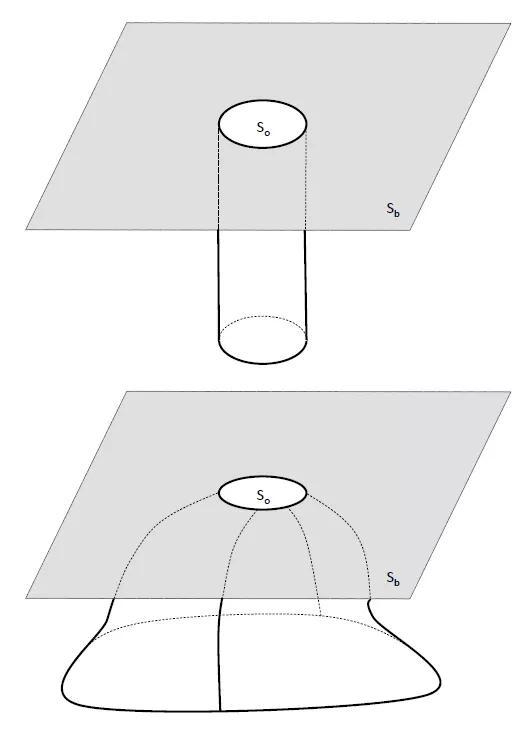
图11.19：将声学组件连接到半无限空间的表面S_o上的非局域边界条件。

本期翻译由西安交通大学能动学院动力工程及工程热物理专业周霜梅同学完成，由MSC Actran产品业务发展经理周泽校对，在此表示感谢！