《线性声学基本现象》声辐射（第三部分）

各位读者看到的如下系列声学知识连载，是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique linéaire》（《线性声学基本现象》）的中文翻译。

11.3 赫姆霍兹积分方程（Helmholtz integral equation）

11.3.1  有界域（Bounded domain）

  

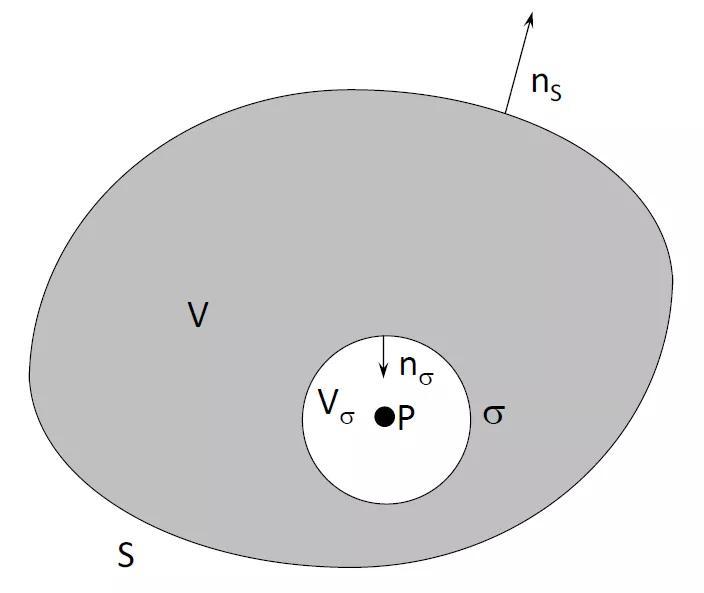
图11.11：关于内部问题的赫姆霍兹方程。情况1：点P在域V内

考虑一个以S为边界的域V。边界面S的法向向量均是指向远离V的方向（见图11.11）。赫姆霍兹积分方程表示为：

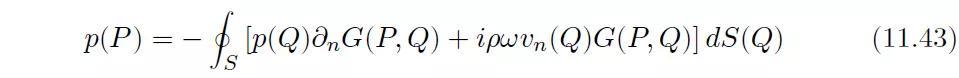
其中Q是边界S上的一点，p是声压，

是法向速度，而G是与赫姆霍兹方程相关的格林函数：

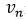
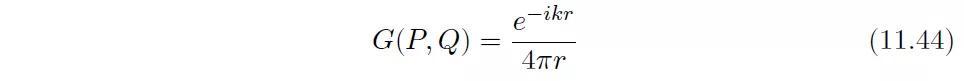
其中r是点P与点Q之间的距离。赫姆霍兹积分关系式将会在接下来的内容中推导。

格林恒等式（Green’s identity）

      考虑两个在域V内和面S上均充分连续且可微的函数u和v。格林恒等式将u与v在体积V与表面S上的积分联系起来：

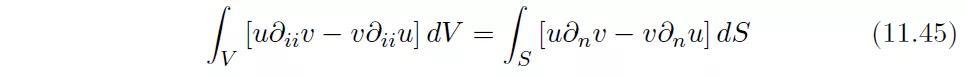
格林恒等式可以用分部积分法来证明，其中需要两次使用高斯散度定理：

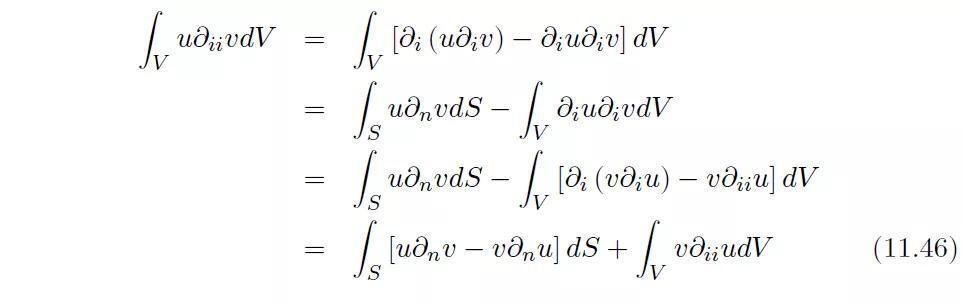
情况1：点P在域V的内部

用压力场p和格林函数G分别替换函数u和v。由于G在点P(r=0)处是奇异的，故我们不能将恒等式应用在整个域V中，而不得不以点P为球心、以面σ为边界划出一个小球域

。然后我们有：

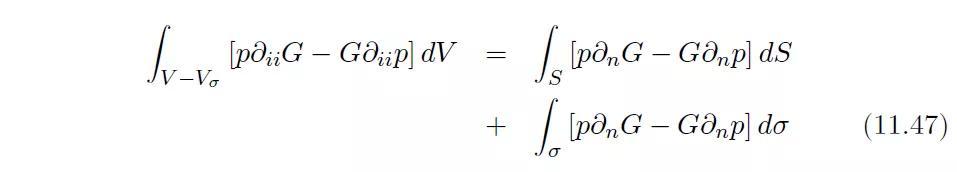
当p和G是齐次赫姆霍兹方程在域

上的解时，上述积分为零：

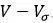
在球面σ上的积分可以被明确计算出来。设ε是球面σ的半径，则函数G（或p）在球面σ上的法向导数与其对ε的导数等值反号：

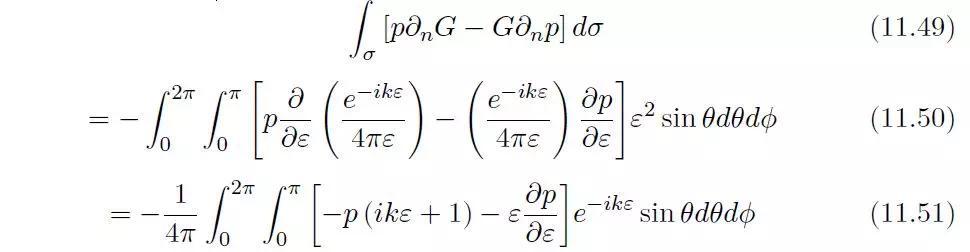
当ε趋向于零，则许多项会消失，然后有：

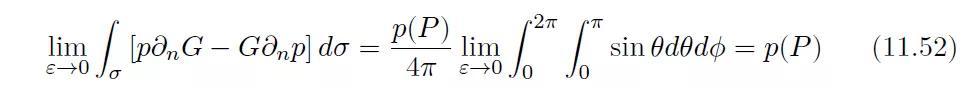
从上式可以看到，在球面σ上的积分最终会趋向于在点P的声压。将式（11.52）和式（11.48）代入方程（11.47），则有：

且如果我们用法向速度代替压力梯度（见式（6.5）），则会得到如下的赫姆霍兹积分方程：

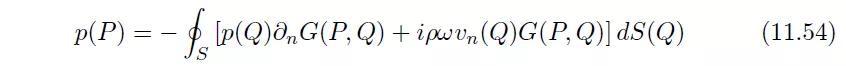
情况2：点P在边界面S上

如果点P位于域V的边界面S上（图11.12），则σ不再是一个完整的球面，而是一个球面的一部分。在面σ上的积分不再等p(P)，而是等于：

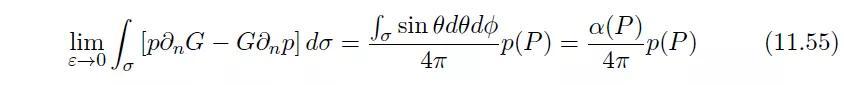
其中α(P)是点P对域V的“立体角”。关于立体角的例子：当在点P处的边界面是规则的，则α(P)=2π；当点P在立方体的边线上，则α(P)=π；当点P在立方体的角点上，则α(P)=π/2。对于在边界面S上的点P的赫姆霍兹方程最终写成如下形式：

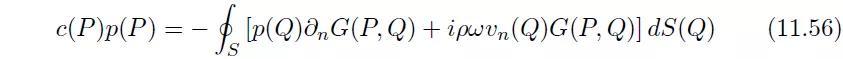
其中c(P)=α(P)/4π，是一个取决于边界面S在点P处的拓扑结构的系数。

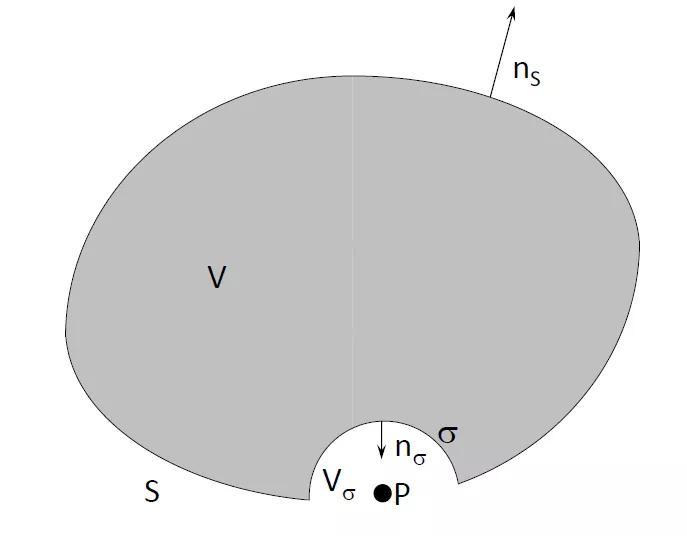
图11.12：关于内部问题的赫姆霍兹方程。情况2：点P在边界面 S上

情况3：点P在域V的外部

如果点P既不在域V内也不在边界面S上（图11.13），那么在积分域V中就没有需要排出的奇异点。然后我们可以得到如下式子:

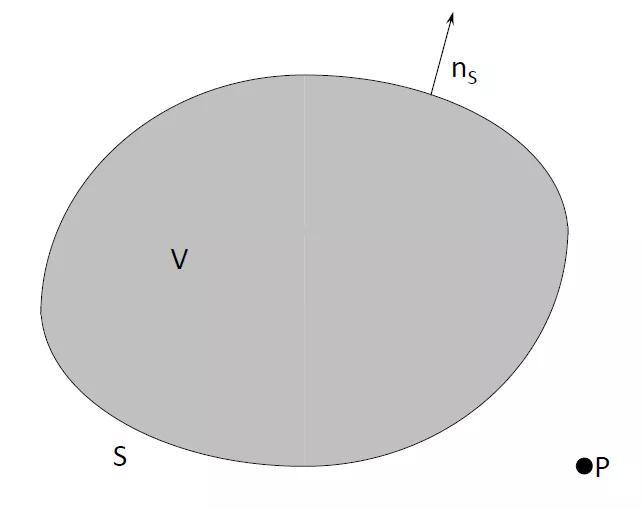
图11.13：关于内部问题的赫姆霍兹方程。情况3：点P在域 V的外部

注意：

1.   式（11.54）和式（11.56）在本质上是不同的。式（11.54）表示的是域V中的压力完全由边界面S上的压力和法向速度分布决定。当已知面S上的p和

，则在域V内的声场就是可知的。方程（11.56）则是将边界面S上的压力分布和速度分布联系起来的一个积分方程。

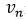
2.   如果面S的法向被定义为指向域V内部，则在面S上的积分的符号就会改变。那么赫姆霍兹方程就写成如下形式：

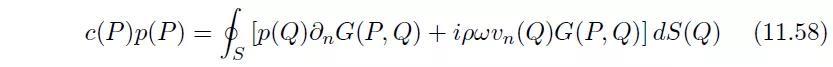
11.3.2  无界域（Unbounded domain）

图11.14：关于外部问题的赫姆霍兹方程。情况1：点P不在界面 S上

考虑一个如图11.14所示的无界域。界面S的法向方向改变了，因为它必须指向域V的反方向。在界面S和σ上的积分依旧按照上述方式计算。还有一个额外的积分出现在无限大界面∑（可以理解为一个半径趋向于无穷大的球面）上。最终，赫姆霍兹积分方程如下：

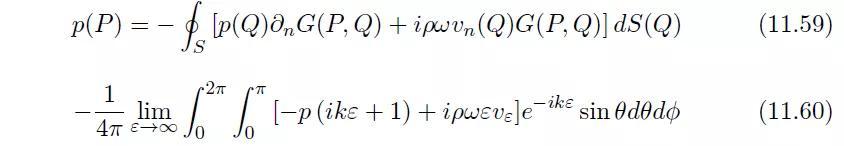
当如下形式的索末菲条件（Sommerfeld condition）被满足时，上式积分为零。

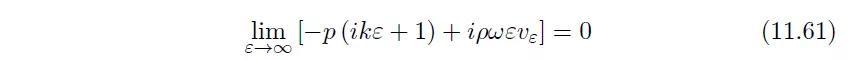
该条件对径向声阻抗施加了如下渐近特性：

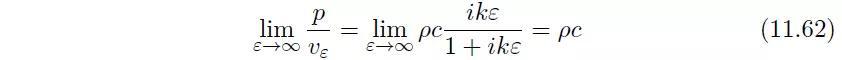
如果点P在界面S上，则赫姆霍兹积分方程如式（11.56）所示。系数c(P)=α(P)/4π取决于点P对外部界面S的立体角α。例如：当在点P处的表面是规则的，则c(P)=1/2；当点P在立方体的边线上，则c(P)=3/4；；当点P在立方体的角点上，则c(P)=7/8。

11.3.3 积分方程的间接形式

考虑一个薄曲面S，其法向向量为n（图11.15）。为了在曲面S上应用赫姆霍兹积分方程，我们必须用一个由

（与n同向）和（与n反向）组成的封闭曲面将面S包围。假设代表着板边缘的面没有几何扩展，则在上的所有积分都等于零。

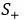
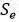
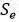
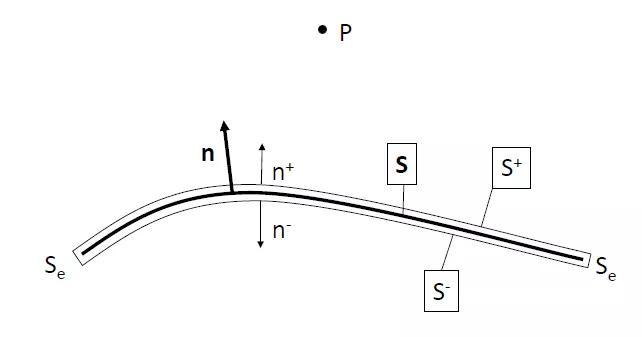
图11.15：用于推导间接赫姆霍兹积分方程的符号

故在P点的压力被表示成如下形式：

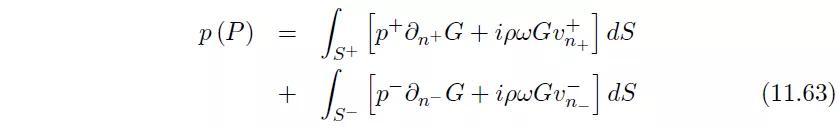
而考虑到：

因此有：

或者，用σ和μ分别表示板S两侧的速度差和压力差，则有：

对比电磁理论,σ被称作单层势，而S被称作双层势。若板S两侧的压力和速度均是已知的，那么就可以通过方程（11.65）得到域内任意一点的压力。这个新的积分方程是一般性的，适用于任何曲面S（开的或闭的，简单的或多重连通的）。如果S是闭合的，则方程（11.65）对于点P在S内还是在S外均是适用的。当P属于S时，奇异积分必须用特定的技术来求得，这里不再赘述【3】。

最后需要注意的是，如果S代表的是薄板的中面，σ（薄板两侧的速度差）通常为零，则得到如下式子：

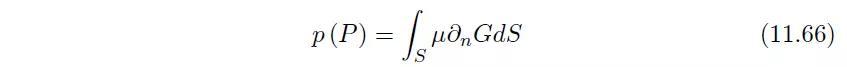
【3】参考2000年由Computational Mechanics Publications Ltd（计算力学出版社）出版的Migeot J-L., Lecomte C., Meerbergen K.的《Implementation and accuracy issues in Boundary element methods in Acoustics（声学中边界元法的实现与精度问题）》。

本期翻译由西安交通大学能动学院动力工程及工程热物理专业周霜梅同学完成，由MSC Actran产品业务发展经理周泽校对，在此表示感谢！