《线性声学基本现象》声辐射(第二部分)
各位读者看到的如下系列声学知识连载,是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique linéaire》(《线性声学基本现象》)的中文翻译。
11.2 多级展开(Multipole expansion)
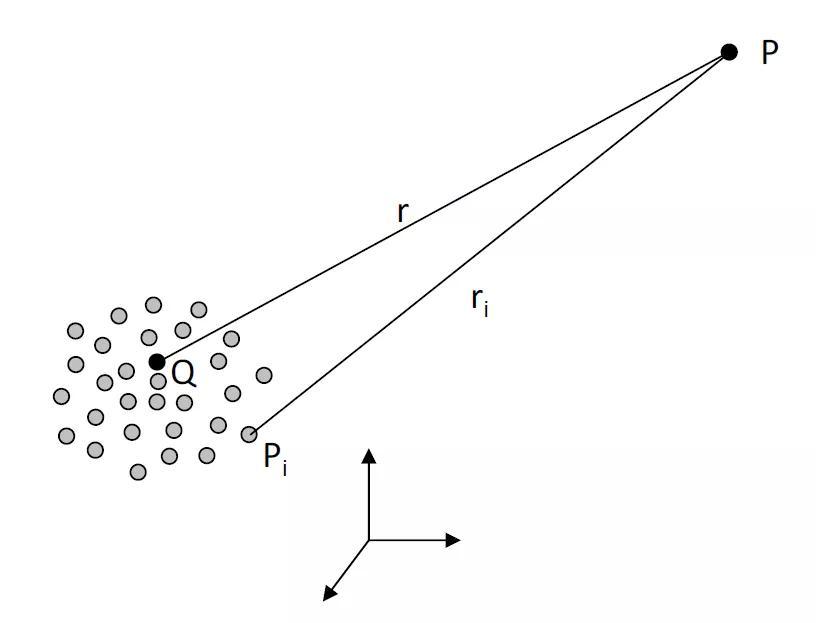
图11.6:用于推导声场的多极展开的符号
考虑位于点
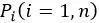
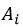
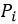
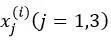
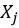

其中
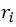

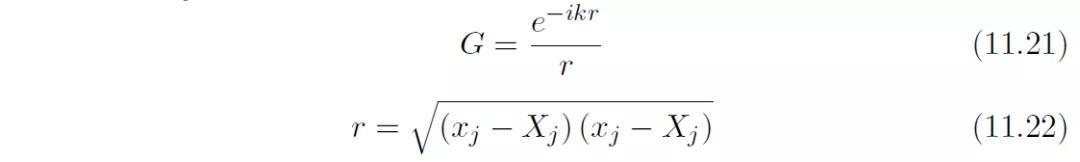
对于每一个点声源,项
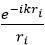
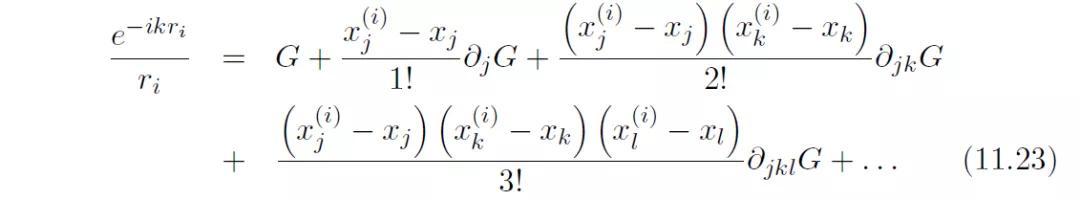
因此,总声压可以被表达成如下形式:
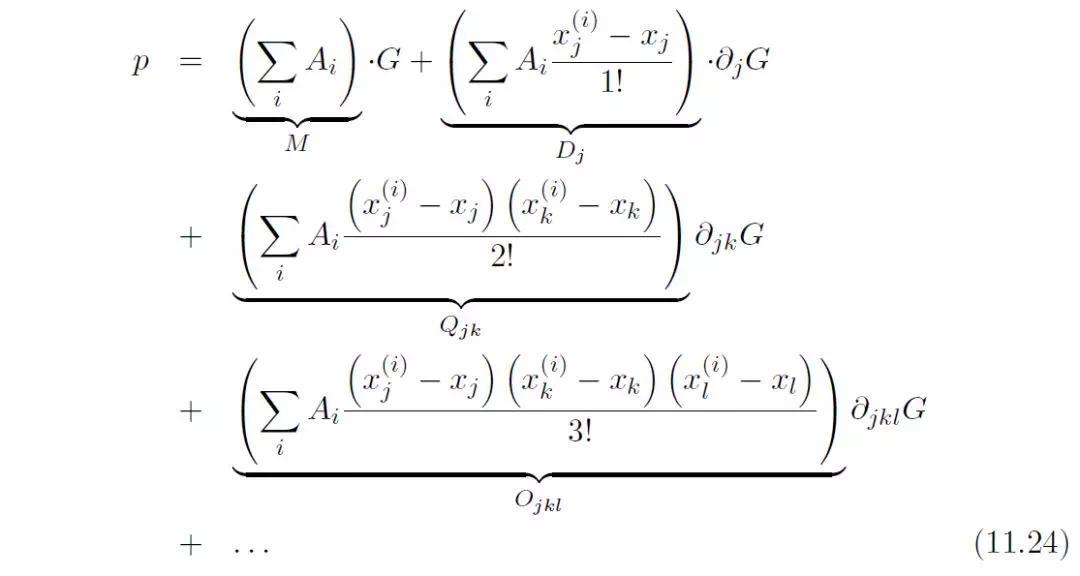
上述表达式可以被写成更加简洁的形式:
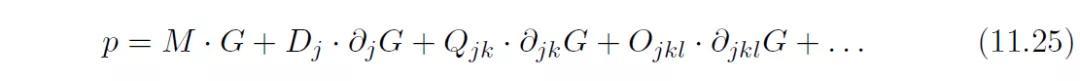
其中M,
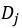
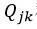
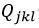
G的偏导数
G对坐标轴的连续偏导数计算如下(注:
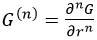
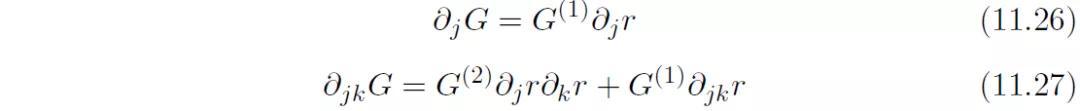
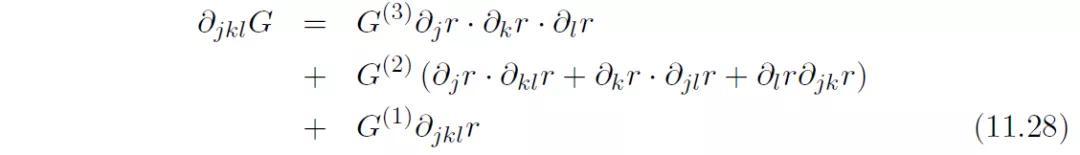
G对r的偏导数
G对r的连续偏导数均是如下形式:
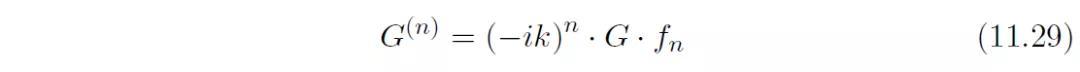
其中函数
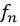
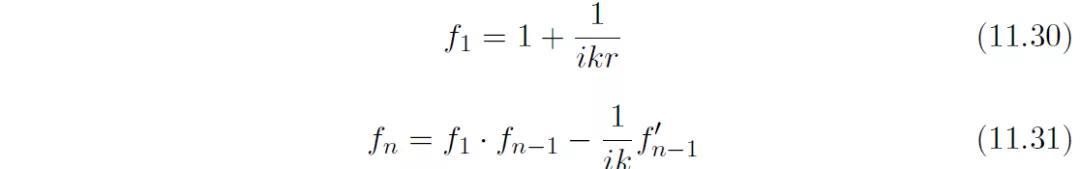
我们发现,当n=1,2,3时,有:
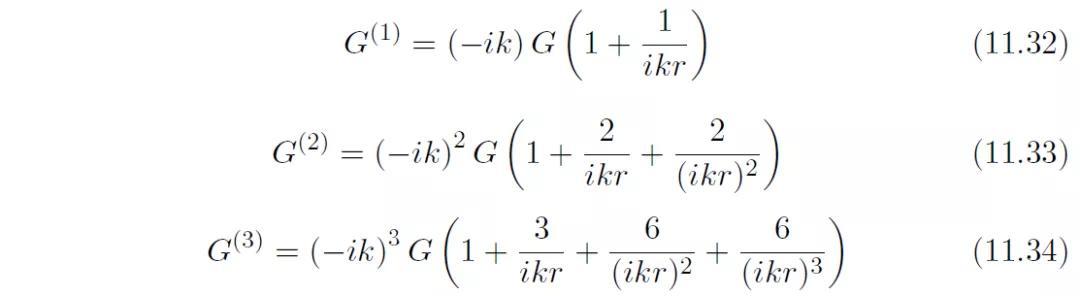
r的偏导数
r对坐标轴的连续偏导数如下:
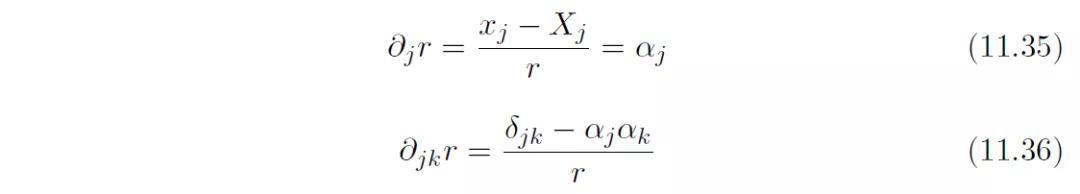
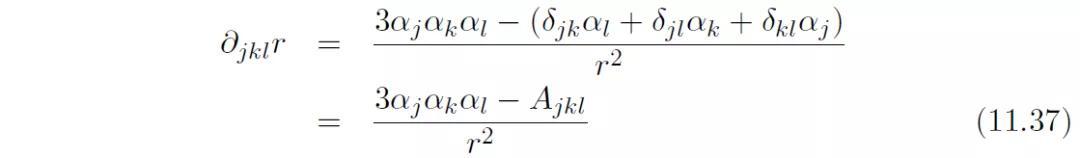
其中,我们定义:
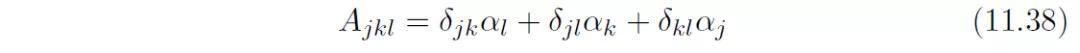
辐射声场的简洁表达形式
最后,完整的声场可以用一个非常紧凑的形式表示,为四个因子的乘积:
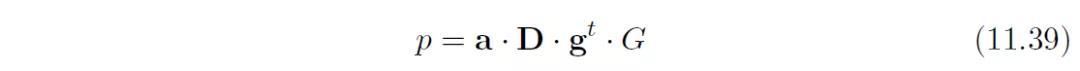
矢量a由连续的多极矩和对应的-ik的幂次的乘积组成:
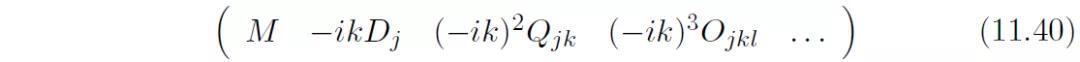
矩阵D由声场的方向性分量组成:
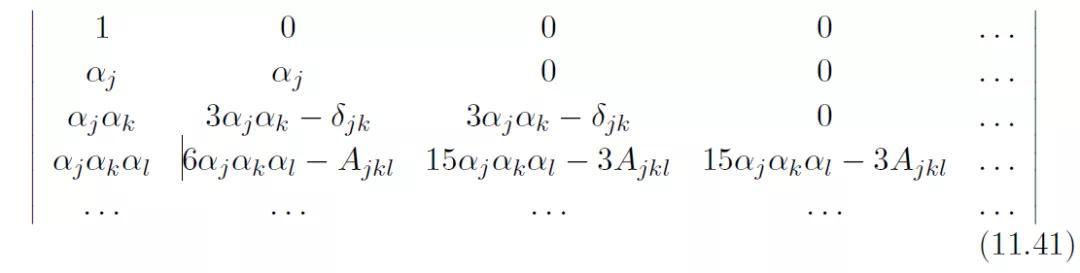
该矩阵的元素是
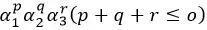

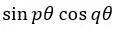
矢量g由
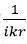

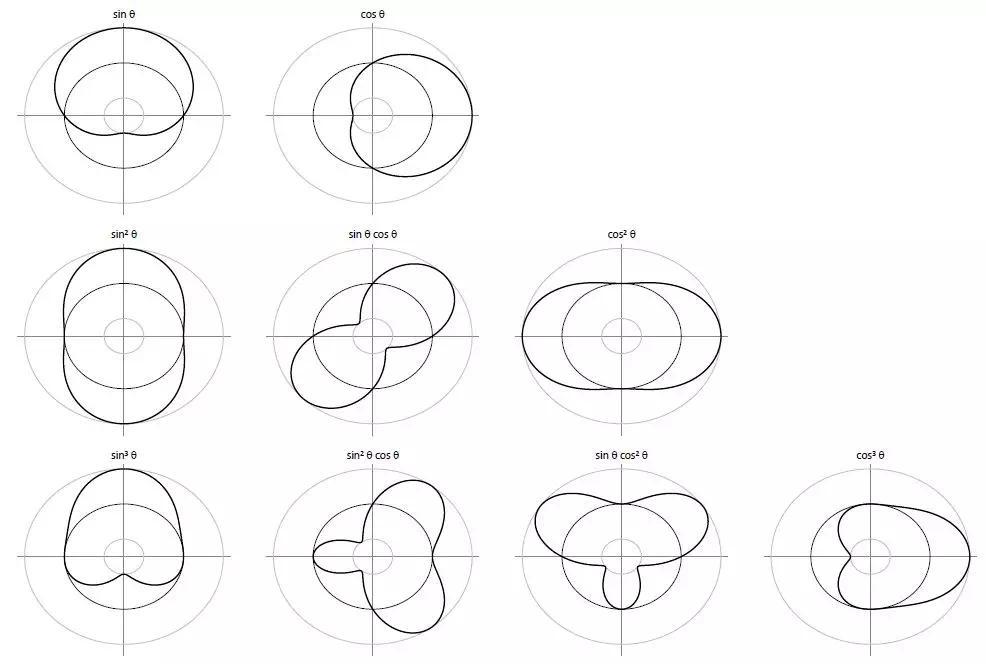
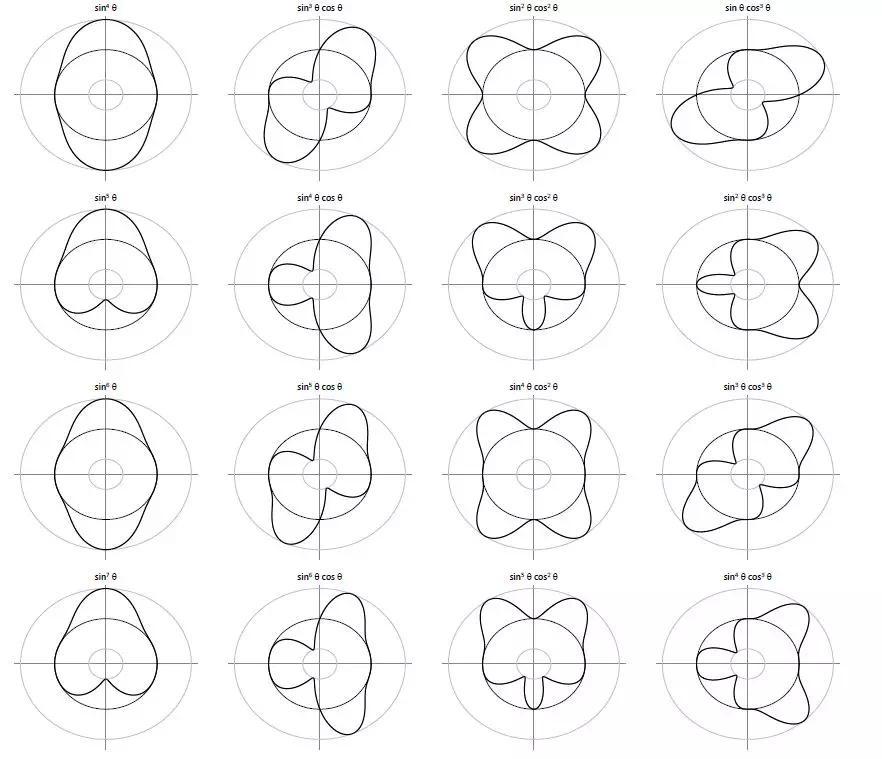
图11.7:基本指向性图(

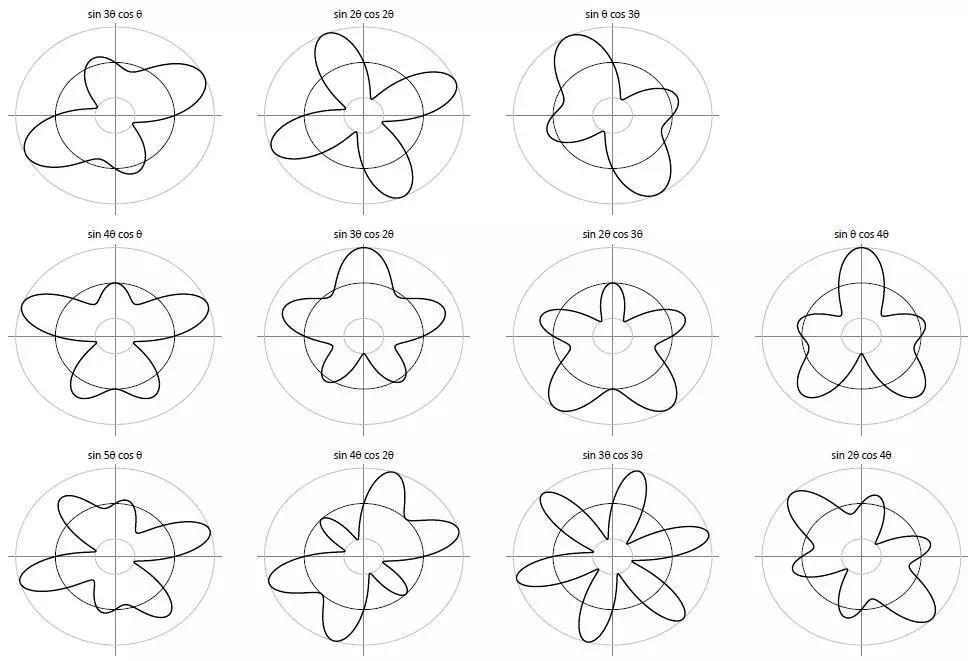
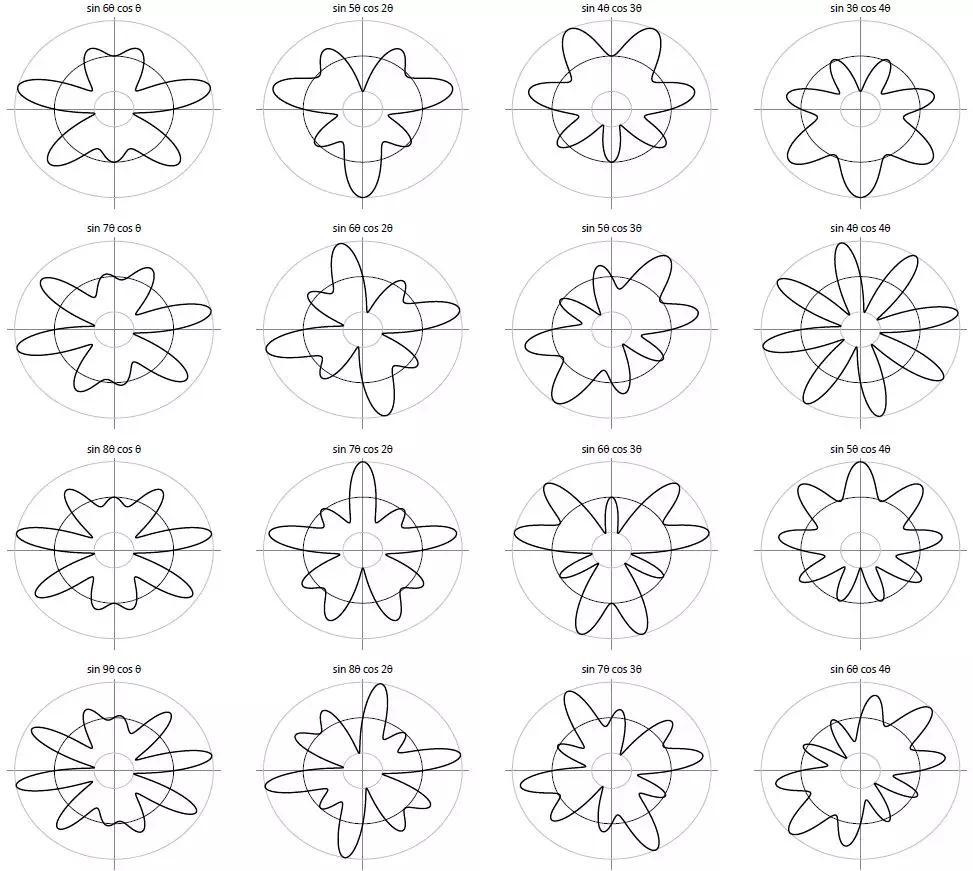
图11.8:基本指向性图(
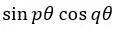
从上述图中,可以观察得到如下重要的结论:
1. 由一组确定的声源(矢量a)所产生的声场可以根据其在给定方向(即对于给定的D矩阵)上的径向衰减来分析,亦可通过观察其在给定半径的球面(即给定的g矢量)上的分布来分析。
2. 在给定的方向上(即对于给定的
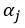
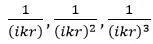
3. 衰减速率与距离r无关,而与无量纲数
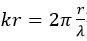
4. 随着距离的增加,第一项很快成为主导项,这是由于其他阶数项衰减速度更快 (当kr加倍时,第1阶减少6 dB,第 2阶减少12 dB,第 3阶减少18dB …)。
5. 复杂声源周围的声域由两部分组成。近场(near field),其g矢量的不同分量具有同等重要性;在远场(far field),g矢量的
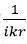
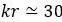
6. 在距声源一定距离r时,声场的方向性是矩阵D的元素的线性组合(系数为复数)。
7.在距离声源很远的地方,第一列的项占主导地位
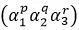
8. 对于给定多极矩(向量a)的声源分布,n阶项的相对重要性随着
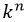

11.9:频率对方向性图的影响:在半无限平面上开口的管道。© ACTRAN by Free Field Technologies。
多级展开的相关性
多极分析的相关性源于这样一个事实,即任何噪声源都可以用等效的单极子点声源分布代替。考虑一个已知法向速度
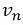
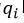
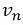
在这个过程中,单个源的振幅取决于频率。相关的多极矩也依赖于频率。高阶项的重要性随着频率的增加而增加【2】。这加强了系数
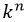
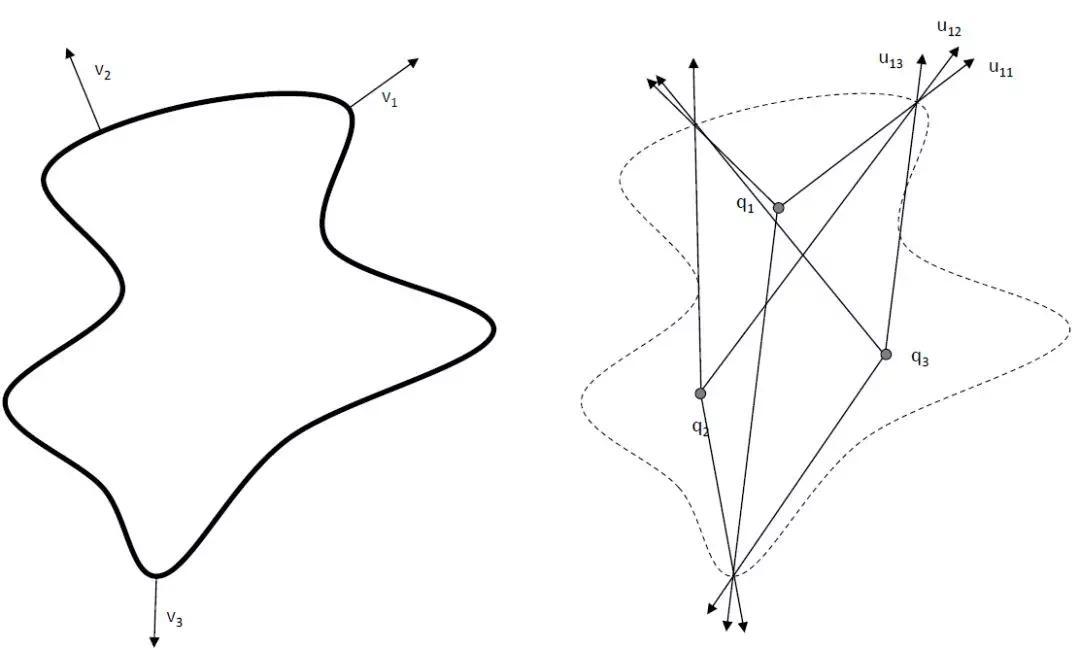
图11.10:任何振动结构都可以用一组等效的点源来代替。右图中三个点源的振幅q1、q2和q3可以设置为与左图中的振动表面上三个不同点的法线速度相匹配。这里只显示了三个声源,而通常需要数百个声源来匹配振动表面的速度分布。用一组等效点源代替振动表面是渐近收敛的;这里就不演示了。
【1】在这一推导中,将使用爱因斯坦关于重复指标隐式求和的约定。见3.2节。
【2】在振动声学中,这反映了一个事实,即更高频率的振动更复杂且包含更高阶模态。
本期翻译由西安交通大学能动学院动力工程及工程热物理专业周霜梅同学完成,在此向周同学表示衷心的感谢!

.png?imageView2/0/w/120/h/120)
.png?imageView2/0/w/90/h/90)

