《线性声学基本现象》声辐射(第一部分)
本文摘要(由AI生成):
本文是声学理论书籍《线性声学基本现象》的中文翻译,重点研究声辐射,特别是自由场中的辐射。文章介绍了两种分析方法:多极分析和亥姆霍兹积分方程。多极分析提供了声场分析的一般框架,将声源看作多极子的组合,并预测了声场指向性的演变。亥姆霍兹积分方程则关联了声场与辐射表面上的声压及法向速度分布。文章还详细讨论了偶极子和四极子的声场特性,包括其指向性和声压分布。
各位读者看到的如下系列声学知识连载,是对于2015年出版的声学理论书籍法语版《Phénomènes fondamentaux de l’acoustique linéaire》(《线性声学基本现象》)的中文翻译。
“生命的目的不在于占有能量,而在于将它辐射。
——亨利 ·米勒 (1891 – 1980) 《战后星期天》(1944)”
本章将研究声辐射,并描述由振动结构产生的声场在没有障碍物的无 界域中的辐射(自由场辐射)。本章提出了两种分析方法:多极分析和亥姆霍兹积分方程。
多极分析(Multipole analysis)为辐射声场提供了一般的分析框架。它表明任何声源都可以看作是单极子声源的组合,并且这个组合还可以被简化为一个单极子,三个偶极子,六个四极子和更多的高阶多极子。多极分析表明,声场的方向性(即在围绕辐射物体的球面上声场的空间分布)是标准基本的声场指向性的线性组合。它还预测了声场指向性随频率和距离的演变过程。多极分析构成了有限元方法向无 界域进行扩展的重要基础:无限元方法。
亥姆霍兹偏微分方程可以重构成边界积分方程(boundary integral equation),该方程将声场与辐射表面上的声压及法向速度分布联系起来。亥姆霍兹积分方程构成了声学中另一种重要数值方法的基础:边界元法。
11.1 偶极子和四极子(Dipoles and quadrupoles)
11.1.1 偶极子
考虑相对于坐标点Q (x, 0, 0)对称的两个幅度相等,相位相反(A 和 –A)的声源(图11.1)。这两个源在坐标点P (x, y, z)处引发的声压是:
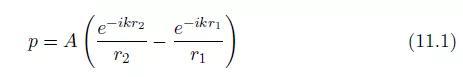
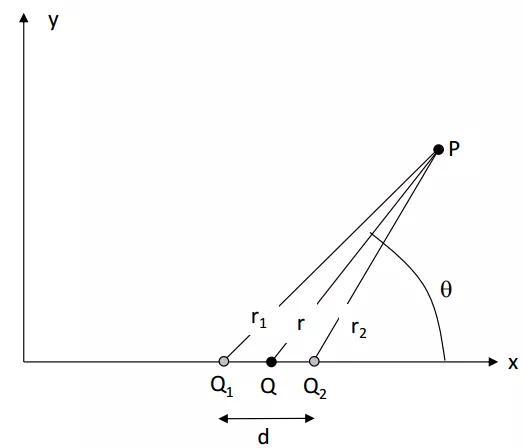
图11. 1:偶极子
如果两个声源之间的距离很小,我们可以将总声压表示为P和Q之间的距离 r以及两个声源之间的距离d的函数:
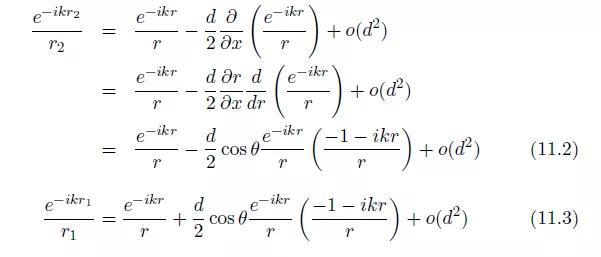

或者,如果d趋向于0,而偶极矩D=Ad不变,则总声压为:
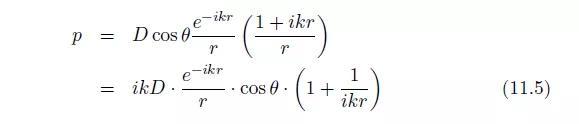
偶极子的声场表现为四个项的乘积:
1. 幅值ikD,它本身是两项的乘积:偶极矩D和偶极子特征因子ik;
2.单位幅值的单极子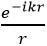 ;
;
3.指向性项cosθ(图11.3);
4. 一个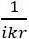 (这里是1阶)多项式,其中当kr趋于无穷时它趋于1。
(这里是1阶)多项式,其中当kr趋于无穷时它趋于1。
偶极子的指向性由两个分别关于偶极子轴上对称的反相叶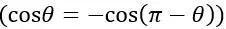 和在对称平面
和在对称平面 上的零声压描述(图11.3)。很容易得到径向质点振动速度为:
上的零声压描述(图11.3)。很容易得到径向质点振动速度为:
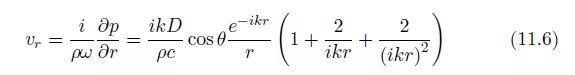
而切向质点振动速度为:
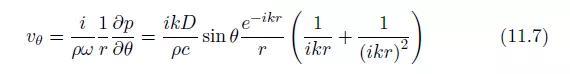
因此得到如下的径向声强:
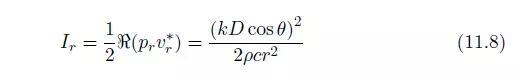
并且通过以Q为中心的球面半径辐射出的声功率为:
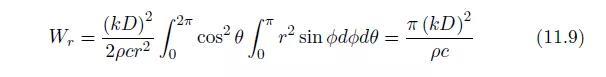
毋庸置疑,该功率与r无关。
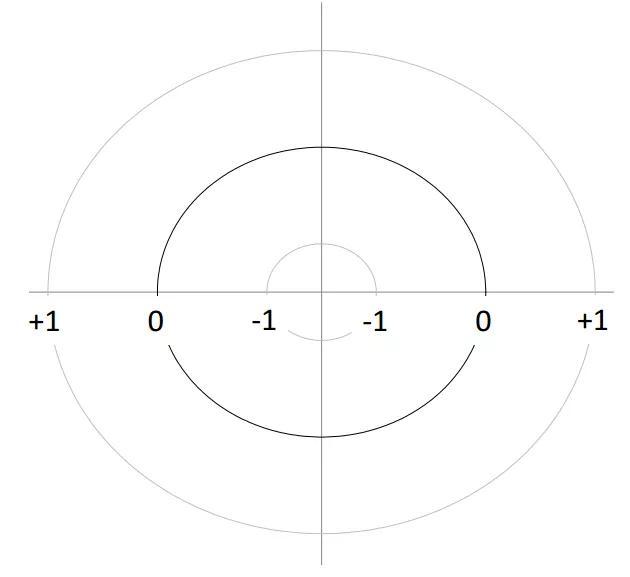
图11. 2:本章中指向性的约定:内圆对应于p = 1,外圆对应于p = +1,中圆对应于p = 0。
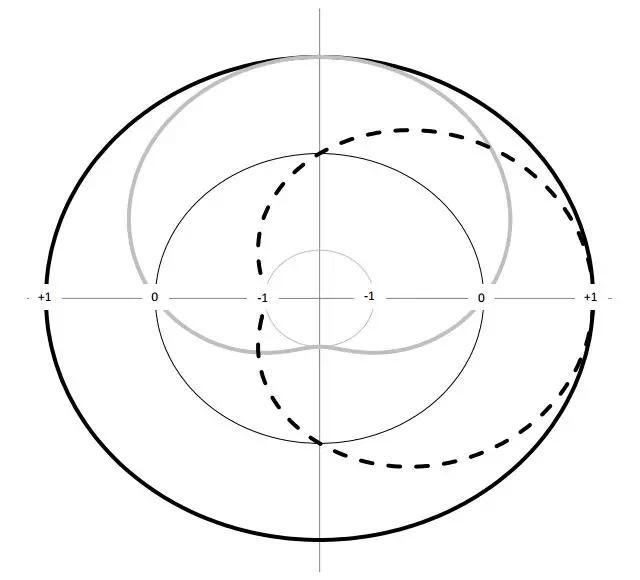
图11. 3:单极子(黑色实线),在x轴上对齐的偶极子(黑色虚线),在y轴上对齐的偶极子(灰色实线)的指向性图。按照图11.2中的约定。
11.1.2 纵向四极子
再次考虑图11.1,不过这次我们会在Q1和Q2放置两个幅度同相相等(A和 A)的声源,并且在Q点放置一个幅值为-2A的声源。则由这三个声源在P点产生的总声压为:
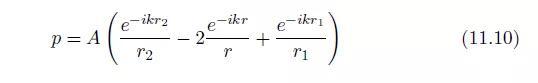
而我们可以这样写:
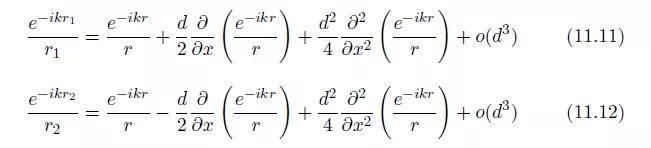
当Q1和Q2间的距离d趋于0,而四极矩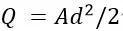 保持不变时,我们发现:
保持不变时,我们发现:
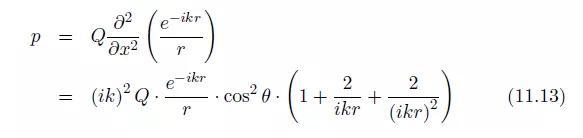
纵向四极子的声场在平面x= xQ(对于在x轴上对齐的纵向四极子)上呈现对称性(这是偶极子场的反对称性平面),而在该平面上的声压为零(图11.5)。四极子的声场同样以四项乘积的形式出现:
1. 振幅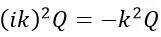 ,它本身是两项的乘积:四极矩和四极子特征因子;
,它本身是两项的乘积:四极矩和四极子特征因子;
2.单位幅值的单极子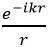 ;
;
3.指向性项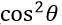 (图11.5);
(图11.5);
4. 一个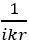 (这里是2阶)多项式,其中当kr趋于无穷时它趋于1。
(这里是2阶)多项式,其中当kr趋于无穷时它趋于1。
11.1.3 横向四极子
考虑位于一正方形四个顶点的四个声源(图11.4)。声源1和4的幅度值为A,另外两个声源的幅度值为-A。在P点得到的总声压为:
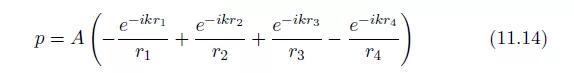
而
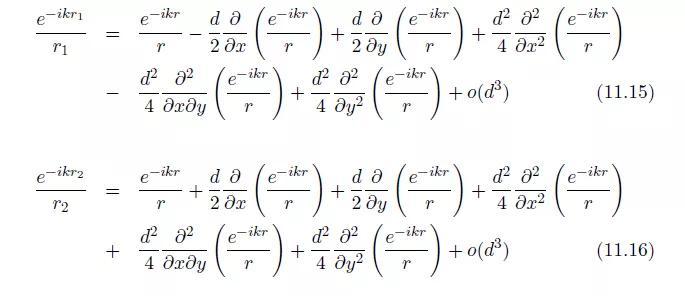
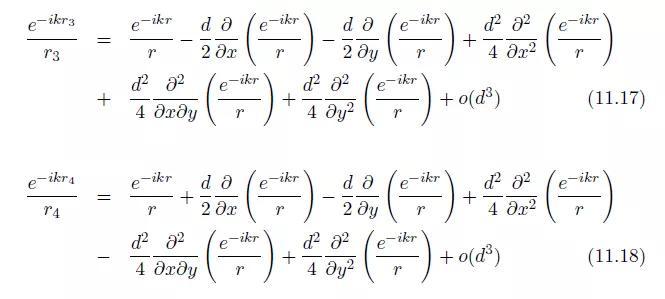
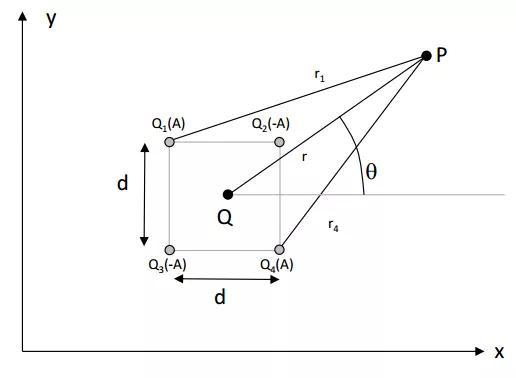
图11. 4:横向四极子。
当使d趋于0而使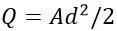 保持不变时,我们可以由上得到:
保持不变时,我们可以由上得到:
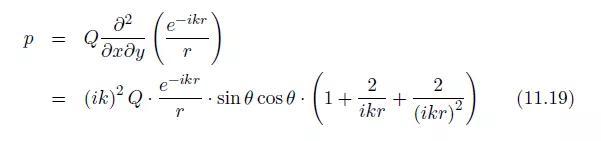
横向四极子的声场有两个对称平面(x = xQ和y = yQ),并且在这两个平面声压为0(图11.5)。
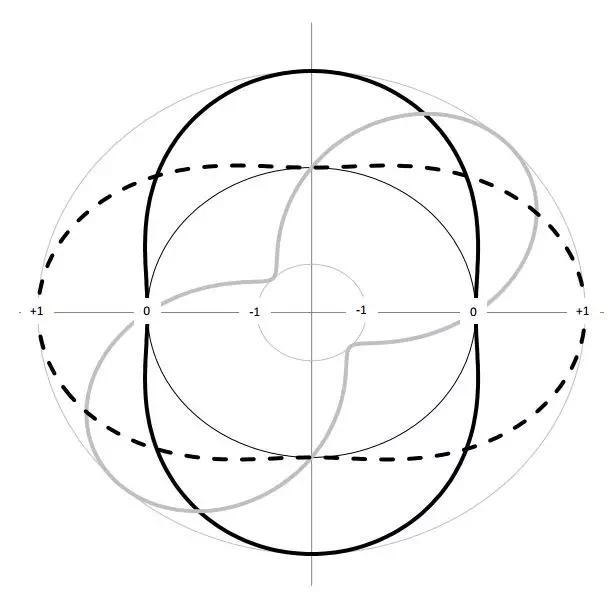
图11.5:三种四极子的方向性图: 在y轴上对齐的纵向四极子 (实心黑线),在x轴上对齐的纵向四极子(虚线黑线)和横向四极子(实心灰线)。。
本期翻译由西安交通大学能动学院动力工程及工程热物理专业周霜梅同学完成,在此向周同学表示衷心的感谢!

.png?imageView2/0/w/120/h/120)
.png?imageView2/0/w/90/h/90)

