飞车走壁中的力学知识

1年前浏览1049

来源：刘延柱科学网博客，作者：刘延柱。

与具有古老历史和传统的其它杂技项目不同，飞车走壁是和自行车、摩托车和汽车等现代交通工具相关，极具时代特征的杂技项目（图1）。上世纪30年代，国人皮德福从英国引进飞车木桶，创立了飞车表演团，以其难度、技巧和观赏性而引起轰动。此后不少省市也相继成立了飞车团队，走壁的飞车从自行车发展成摩托车和小汽车，原始的大木桶也发展成钢制的圆球形网状结构（图2）。观众不必攀登到木桶顶部的边缘向下俯视，就能以任意角度欣赏精彩的飞车表演。上海杂技团的 “时空飞车” 节目中，8个现代化勇士骑着摩托车从四面八方冲进直径6.5米的巨型钢球，高速飞驰穿梭翻腾的表演令观众惊心动魄。

在略带锥度的圆柱形木桶内，骑手在与地面平行的平面内能紧贴桶壁完成圆周运动，是因为桶壁对车轮的摩擦力平衡了车的重力。只要车的重力不超过桶壁的最大静摩擦力就不会掉落。根据库伦摩擦定律，最大静摩擦力与正压力成正比。而正压力来自离心惯性力对桶壁的挤压，与车速的平方成正比。圆柱形木桶内的飞车如偏离水平面，轨迹的曲率就会减小，离心惯性力和正压力，乃至最大静摩擦力都随之减小。因此，骑手在木桶内的运动不能偏离水平面太远。当木桶发展成钢制圆球时，情况就不同了。骑手沿球面内的任意圆弧运动都有离心惯性力存在，它不仅产生正压力和摩擦力，而且沿铅垂轴的分量直接参与了重力的平衡。由于摩擦力和离心惯性力共同分担车的重力，骑手甚至可在过顶点的垂直平面内飞驰，获得更大的自由度。

为分析飞车沿球面内任意大圆弧的运动，以球壁的球心O 为原点，建立固定参考坐标系 (O-XYZ)。Z 轴为垂直轴，X 轴沿运动平面与过O 点水平面的交线（图3）。令 (O-XYZ) 绕X 轴转过α 角，使Z 轴到达的新位置与运动平面的法线轴z 重合。再绕z 轴转过β 角的位置记作 (O-xyz)，x 轴沿球壁的外法线指向车和车手的质心 P，y 轴沿车的速度方向。α 和β 是确定飞车位置P 的两个角度坐标。设载人车的质量为m，速度为v，球面的半径为R，桶壁对车轮的约束力F 作用于前后轮接触点连线的中点Q。设F沿x、y、z 各轴的分量为Fx、Fy、Fz，其中Fx=-Fn 为法向约束力，沿x 轴的负方向，Fy、Fz 为沿切向的摩擦力。离心惯性力mv²/R 沿x 轴的正方向，重力mg 沿Z 轴的负方向。根据达朗贝尔原理列出车体沿x、y、z 各轴的质心运动方程：

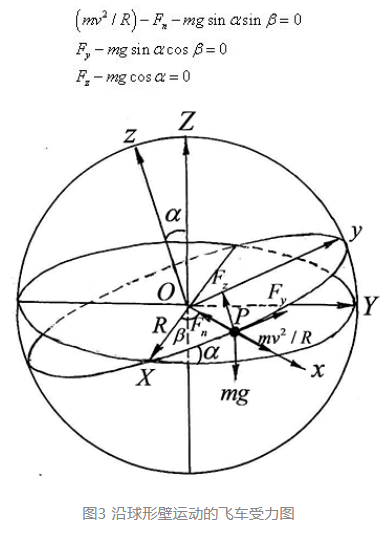
为使车轮保持紧贴球壁的滚动状态，法向的单面约束力Fn 必须为正值，且摩擦力 Fy、Fz 的模必须小于最大静摩擦力。即以下 3 个约束条件必须同时满足：

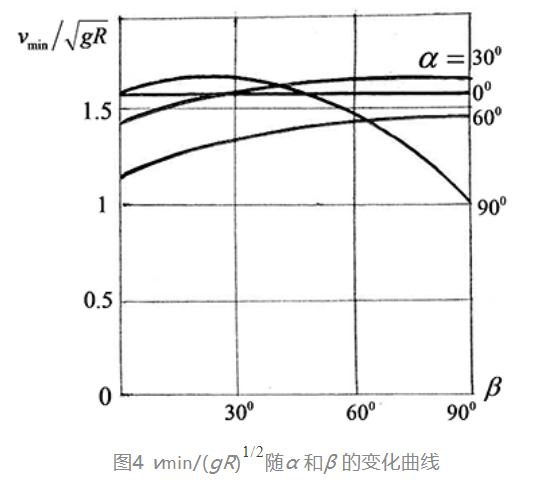
vmin 随α 和β 的变化曲线在图4中给出。作为特例，α=0 是在水平的赤道面内运动的飞车，圆周上各点有相同的最低速度vmin=(gR/f)^1/²。设R=6m，f=0.4，算出的最低速度约为12m/s。对应的加速度v²/R 为24m/s²≈2.4g，超过了重力加速度的两倍。实际上飞车的表演速度大大超过此最低速度，如车速增至18m/s，车手就必须承受5g 以上的加速度。α=90°是在垂直平面内运动的另一特例，最低速度随车体的不同位置而改变。在β=90°的圆周顶端达最小值vmin=(gR)^1/²，此时车的重力完全由离心惯性力平衡。按以上数据算出的最低速度(gR)^1/² 约为8m/s。由此可见，虽然沿垂直面运动的飞车看起来惊险万分，在顶端甚至处于倒悬状态，但必需的最低速度反而比沿水平面的飞车小得多。

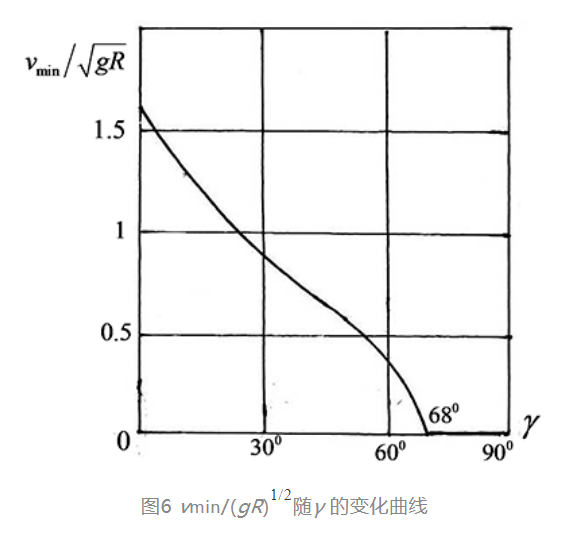
用于飞车的圆筒形木桶相对垂直轴通常有γ=10°左右的倾角而略带锥度。设飞车在桶内作半径为R 的水平圆周运动。以圆心O 为原点，Z 轴为垂直轴，O 点至车的质心P 的连线为水平轴X。令 (O-XYZ) 绕Y 轴转过γ 角，使X 轴和Z 轴到达的新位置平行于接触点Q 处桶壁的法线轴x 和切线轴z，y 轴沿飞车前进方向。参照图5表示的受力状况，仅保留γ 的一次项，列出车在重力、惯性力和约束力作用下沿x 轴和 z 轴的平衡方程：

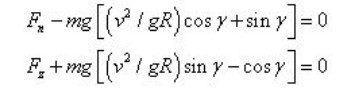
γ 角在0°至90°范围内变化时，为保证车轮紧贴球壁滚动的Fn>0条件可自动满足。飞车的最低速度可从另一条件|Fz|<fFn 得出：

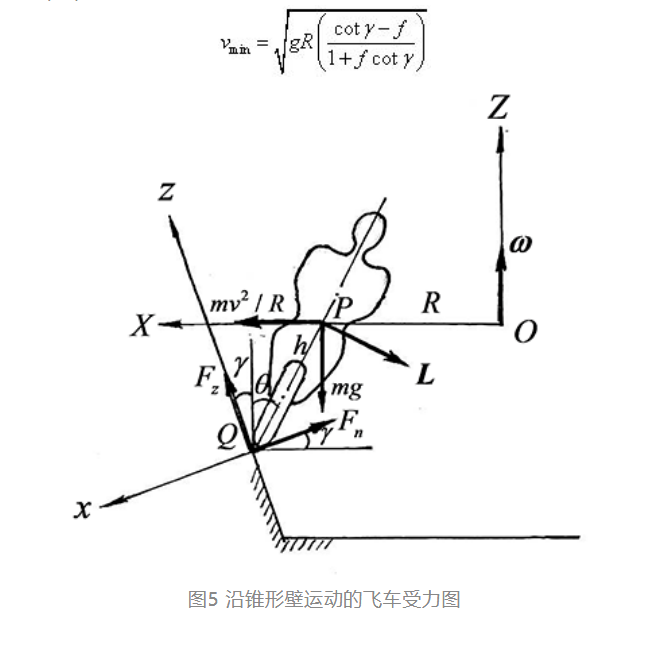
图6为f=0.4时，飞车的最低速度vmin 随γ 角的变化曲线。当γ 增大桶壁趋于平坦时，最低速度随之降低。对于cotγ=f 的特殊情形，即γ=68°或桶壁相对地面坡度为22°的特殊情形，vmin=0。此时重力的切向分量等于最大摩擦力而产生自锁，即使车速接近零也不会下滑。当车在此位置以任意速度行驶时，所产生的离心惯性力均能推动车向上方移动。

类似现象发生在自行车的场地赛。自行车赛场的圆形赛道外圈高于内圈，形成弧形断面，便于使车的重力产生向心力分量。按以上分析，最低速度与半径的平方根成正比，内圈的最低速度低于外圈。当内圈上的自行车手速度过快时，离心惯性力将车向上推至外圈。速度降低时，重力再将车拉回内圈（图7）。

以上在列写力平衡方程时并未考虑力矩的平衡。实际上在运动过程中，重力和离心惯性力作用于质心P，法向约束力和摩擦力作用于车轮与桶壁的接触点Q，P 与Q 并不重合。以水平圆周运动为例，由于离心惯性力与支承力构成一对力偶，车体必须向一侧倾斜，使重力与摩擦力构成方向相反的力偶与之平衡。将P 与Q 的连线作为车的纵轴，相对垂直轴的倾角为θ，设h 为车直立时的质心高度，即P 与Q 之间的距离（图5）。则作用力对质心P 的合力矩M 沿切线轴y 的负方向，模为

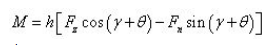
此力矩必须平衡因动量矩改变方向而出现的陀螺力矩Mg

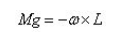
其中，L 为前后车轮旋转产生的对质心的动量矩，沿车轮平面的法线，即x 轴的负方向。如车轮沿y 轴作无滑动的纯滚动，r 为车轮半径，则车轮的角速度为Ω=v/r，设J 为车轮的转动惯量，L 的模为L=2Jv/r。ω 为L 矢量随同车的圆周运动绕Z 轴转动的角速度，模为ω=v/R。根据图5判断，Mg 指向y 轴的正方向。从达朗贝尔原理出发，将

其中，v²/gR 是向心加速度与重力加速度之比，倾角θ 随着速度的增高和圆周半径的减小而加大。如忽略微弱的陀螺效应，则简化为θ≈arctan(²/gR)。将v 以最低飞车速度 (gR/f)^1/²代入，化作θ≈arctan(f )=68°。这就是图1、图2和图7中所有飞驰中的车体都保持倾斜姿态的原因。