管道振动及声传播的研究现状
来源:摘编自《船舶力学》,2001年4月 第5卷 第2期《管道流固耦合振动及声传播的研究现状及展望》,作者:刘忠族 孙玉东 吴有生,中国船舶科学研究中心。
一、管道振动及噪声源的描述
管道噪声是管壁结构的振动和管内流体中声波相互作用,并沿管壁和管内流体传播与辐射的过程。
作用于管道的激励有两种:力激励与声激励。力激励主要是指,泵作用于管壁与流体的动态力;声激励是指,泵的水动力噪声与阀门等处的湍流噪声。湍流噪声是由控制阀和流量调节器产生的,在控制阀和流量调节器处,通流面积突然缩小或扩大,由此产生湍流,在下游伴随着压力脉动。这种脉动压力在流体中向下游传递,从而形成平面波而成为湍流噪声。
对湍流噪声的机理已有许多研究。魏化军等将阀门噪声归纳为三个部分:即单极子噪声源、偶极子噪声源和四极子噪声源,并根据Lighthill四极子理论和流体动力学的基本原理,分析低速气流引起的阀门噪声中湍流声源和产生机理和分布规律。Chadha也研究了控制阀的声学特性。
二、流引起的管道振动及稳定性
管道振动及稳定性主要研究流速对管道系统动力学特性的影响。该研究一般考虑液流与管道之间的相互作用,忽略流体可压缩性,因此又称为液-弹耦合振动。
由于常用管道长径比远大于1,厚径比又不是很小,所以在研究中普遍采用梁模型。十九世纪末,人们开始研究管道振动问题,但研究曾一度停顿。从二十世纪五十年代开始,人们才系统地研究管道振动及稳定性问题,从那以后,围绕该研究的文章层出不穷。在这一研究领域,Paidoussis 和Chen 等学者做了有代表性的研究工作。
若流体为无粘不可压缩的稳定流动,忽视重力、结构阻尼、管道外部拉压力时,等直管的弯曲自由振动方程为

式中,EI 是管道的抗弯刚度;M 是流体的线密度;m 是管道的线密度;![]() 是流体的平均流速;uy 是管道横向振动的位移;z 是管道轴向坐标;t 是时间变量。七十年代,Paidoussis 和Issid 在以上方程的基础上提出了一个更一般的方程,这个方程考虑了管道的轴向拉压载荷、重力、管道的材料阻尼和支撑分布阻尼等。方程的形式为
是流体的平均流速;uy 是管道横向振动的位移;z 是管道轴向坐标;t 是时间变量。七十年代,Paidoussis 和Issid 在以上方程的基础上提出了一个更一般的方程,这个方程考虑了管道的轴向拉压载荷、重力、管道的材料阻尼和支撑分布阻尼等。方程的形式为
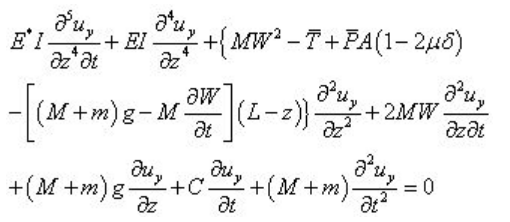
式中,E* 是材料的内阻系数;C 是支承的粘性阻尼系数;δ 是指示管道端部能否移动的因子,非0即1;μ 是泊松比;![]() 分别为管内平均压力和管道端部轴向外载。这一方程是至今为止公认的较为完善的描述输液管道液-弹耦合振动方程。
分别为管内平均压力和管道端部轴向外载。这一方程是至今为止公认的较为完善的描述输液管道液-弹耦合振动方程。
1987年,Paidoussis以“Flow- induced instabilities of cylindrical structures”为题,围绕输液管道振动作了精辟的综述,用十分翔实的内容深入介绍了各种输液管的分叉行为和已取得的研究成果。其中着重指出有两种失稳现象:
发散 (Divergence) 失稳,它属于流引起的屈曲失稳;
颤振 (flutter) 失稳。
具体哪一种失稳形式先发生与支承情况有关,Paidoussis的这篇综述主要还是针对线性问题。
近十几年来,人们在输液管的非线性振动与分叉方面又做了不少有成效的工作,发现了以往在线性范围内从未得到的一些现象。主要包括:
考虑两端固支条件下,由于横向挠度引起的轴向拉力以及大曲率的影响,建立了输液管的非线性运动微分方程;
提出了一些分析非线性动力系统的现代计算方法;
研究了定常流和振荡流作用下悬臂输液管的分叉与混沌行为;
分析了两端支承输液管非线性振动的稳定性以及振荡流导致的参数共振。
时隔6年,Paidoussis于1993年又撰写了一篇综述,引用了200多篇文献,其中花了较长的篇幅介绍和评述了非线性振动方面所取得的近期成果。
当管道的长径比较小,管壁较薄时,管道应采用壳体模型。此时,管道存在壳体模态的失稳,对应的环向波数为n= 2,3,… ,而不是n=1的梁模态。事实上,环向波数n=1的振动也是壳体模态,但它可以用梁的横向振动来近似代替。管道壳体模态的失稳现象是Paidoussis 和Denise 首先发现的。1972年,Paidoussis 又利用Flǜgge 方程和不可压缩势流理论研究了输液圆柱壳的稳定性问题,从能量的观点对圆柱壳的颤振失稳给予了解释。黄玉盈等研究了不可压缩势流与正交异性输液圆柱壳的耦合振动及稳定性问题,得到了与Paidoussis 相类似的结果。Nguyen 与Paidoussis 等研究了两个同轴圆柱壳间存在粘性层流时,引起的圆柱壳的振动及稳定性问题。
对曲管的研究存在两种理论:不可伸缩理论和可伸缩理论。有关这方面李琳作了详细的综述。
三、非流动因素引起的管道振动
非流动因素引起的管道振动是指忽略管内流速的影响,而将管道振动归因于压力、流量的脉动、水锤及机械激励等因素。
水锤源于定常流的突然变化,如阀门的快速开关,泵的起动与停止等。经典水锤分析中,管道的弹性仅仅引入压力波的传播速度中,管壁的惯性和轴向运动没有考虑,这对于全管刚性固定的管道是可接受的。
管道振动要考虑流固耦合作用 (FSI),其三种耦合机理为:泊松耦合、连接耦合、连接耦合与摩擦耦合。对于管道系统在激励作用下的响应问题,摩擦耦合可以忽略。
经典水锤理论只考虑流体运动,忽略管壁弹性的影响,得到二方程模型:
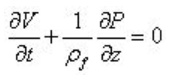
60年代,随着计算机的出现,有了MOC法求解水锤方程的标准方法。
压力波速是首先涉及的问题。自由流场声速为

不可压缩流体在弹性管中

可压缩流体在弹性管中
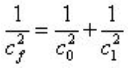
将自由流场声速公式和不可压缩流体在弹性管中的公式代入上式中,得到
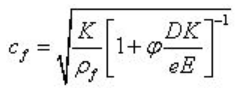
在推导上式的过程中,Korteweg(1878) 认为管道是由一系列无质量的环组成,这些环随着管内流体的压力P 的变化而收缩和扩张。
Korteweg指出:其理论对长波有效,当考虑管壁的轴向应力时,泊松比的影响必须考虑,管壁的轴向惯量也要考虑。由泊松耦合产生的轴向应力波沿管道传播。Korteweg 也研究了径向惯性力的影响,发现对于短波,流体与管道的径向惯性同样是重要的,由此导致波速随波长发生变化。Lamb(1898) 完整地研究了充液管道的轴向和径向振动,他考虑了泊松耦合的影响,推导了关于波传播相速度与波长关系的频散方程。对于长波,流体中的压力波和管壁中的轴向应力波是主要的,波传播速度分别收敛于cf 和ct,其中
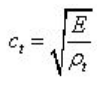
径向振动只是对于短波才重要。
Halliwell(1963) 根据经典水锤理论推导了分别薄壁管和厚壁管中压力波的传播速度,认为教科书中存在不同波速的原因是由于管道不同支承条件引起的。三种支承条件是:
管道锚固但各点可以轴向移动,ψ= 1;
管道锚固各点不能轴向移动,ψ= 1- v²;
管道只在上游端固定,ψ= 1- v/2。
Burmann(1980) 认为对于短管和尖峰波壳体理论是必要的,他将扩展水锤理论与管壁的轴向应力波结合起来,推导出下面的四方程模型:

在推导该方程时,利用了以下二方程:
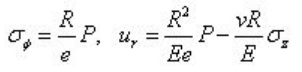
Walker 和Phillips(1977) 研究了短波长压力脉冲在弹性直管中的传播,包含泊松耦合与连接耦合,考虑了管壁的径向惯量和流体的附加质量,从而产生了两个附加方程:
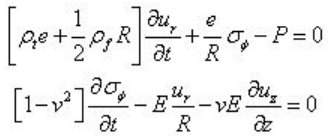
以上六方程模型,利用MOC法可以求解。
密西根州立大学的Wiggert 与Hatfield 合作处理充液管道系统的FSI问题。Hatfield 将分量综合法 (Component- Synthesis Method- CSM) 引入频域响应分析,从原理上说,时域响应可以由频域响应通过Fourier反变换实现,但非常困难。Wiggert 提出了十四方程模型,除了考虑管道与流体的轴向压缩波和管道的扭转振动外,还用Timoshenko 梁方程描述管道的弯曲振动,用MOC法求解。理论结果与实测结果吻合非常好,证明十四方程模型对于分析空间管系振动及压力波的传播是完全正确的。
四、管道系统声传播
管道系统研究的另一个领域是管道对振动及声的传播特性及衰减规律。一般情况下,管壁与流体都存在阻尼,振动在传播过程中要发生衰减。研究管道振动及声传播的目的就是要了解振动和声传播的规律,从而寻求合理的控制方法。
对于管道声传播,一般只在管道轴向考虑流体可压缩性,而在横向不考虑流体的可压缩性。在低频振动时,管道内的波当作平面波来处理。
1981年,Cabelli 和Shepherd 研究了不同几何参数时,弯头对声波的反射和向前传播。通过利用FEM方法求解二维Helmholtz 方程,获得反射声模态幅度向量以及与透射声有关的传递矩阵。
1995年,Feng 研究了直管道内壁上铁锈和空气的混合层对声波的吸收作用,解释了输液管道在高频段声传播的理论结果与实验结果的矛盾。结论指出:这一薄的吸收层降低了高频段振动和噪声的水平,但对声波的轴向传播速度没有影响。在管道内壁均匀地涂一层吸声油漆或焦油,可以将振动或噪声降低大约10dB。
国内学者在管道声学方面也做了很多研究工作,朱之墀等发展了圆管中三维声场的计算技术。
五、管道振动及脉动压力传递的计算技术
单跨梁或连续梁的振动问题可利用Galerkin法求解。而对于空间管系必须寻求有效的数值计算方法。常用计算方法是:有限元法、特征线法、传递矩阵法、阻抗分析法和模态综合法。其中,传递矩阵法由于自由度少,占用计算机内存小,程序上容易实现,比有限元法更为优越。另外,将空间管系划分为若干个单元,在每个单元内部采用有限元方法描述,而单元之间用传递矩阵法连接,这样形成的迁移子结构法对于处理管道动力学问题也是好方法。
1 有限元法
空间管系计算中一个有潜力的方法是基于梁的精确有限元格式,即利用微分方程的精确解代替多项式的插值函数,从而一个复杂系统用少数几个单元就可模拟。
基于液流梁的有限元方程与普通梁的有限元方程相比,系统的自由度数不变,但由于流速的影响在液流梁的有限元方程中出现了陀螺矩阵,一般采用状态空间求解。
1997年,Olson 从简单到复杂对直管与管内流体的耦合振动的有限元法进行了综述,着重阐述采用梁单元计算管道流固耦合问题的基本思路。
2 特征线法
这是一种时域差分方法。蔡亦刚以流体的压力P 和流量Q 作为基本未知量,列出两个偏微分形式的波动方程如下:
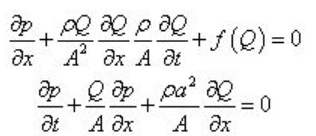
通过特征线方法获得了管道的瞬态响应。Wiggert 等考虑了空间管道系统中典型管单元的五族波,涉及十四个状态分量,列出十四个运动微分方程,同样是利用特征线法进行了求解。这五族波分别是:
管壁和流体介质的轴向压缩波(两族);
管壁横向剪切波(一族);
梁的横向弯曲振动(一族);
管壁的扭转波(一族)。
对于各向同性材料直管,以上五族波中,扭转波与剪切波不发生耦合;弯曲振动与介质的轴向压缩波不存在耦合作用。
3 传递矩阵法
传递矩阵法可应用在时域或频域,时域传递矩阵法是一种直接方法。1975年,Bickford 等用传递矩阵法分析了平面曲梁的振动,其中考虑了转动惯量、剪切变形和轴线可伸缩性的影响;1980年,Sato 等用传递矩阵法分析了Euler- Bernoulli 梁的振动;同年,Irie 利用Timshenko 梁模型对输流管道振动和稳定性问题的传递矩阵法进行了推导。Lesmez 和Wiggert 等对空间管道系统振动的传递矩阵法做了开创性工作,在推导过程中利用分离变量法,最后形成的系统特征矩阵中含有特征值ω。该方法适用范围广,应用灵活,是解决空间管系振动及声传播的理想方法。
关于空间管道系统的传递矩阵法,考虑了上面提及的五族波,用十四个状态参量描述管壁结构与管内流体的运动。空间管道系统的传递矩阵法包括场传递矩阵和点传递矩阵的推导。
4 阻抗分析法
阻抗分析法与传递矩阵法的形式是类似的,按照管道系统的构成划分成若干单元,每个单元的端面用速度和力构成的矢量作为其状态向量,这样,单元场矩阵的元素是阻抗参数。该方法也是一个适用方法。用阻抗法分析空间管路系统的振动与声传播问题,其状态向量只要十个分量就可以了,用这种方法处理管道系统的声传播问题将会更有效。蔡亦刚在这方面作了一些基本的研究,他选择流体的压力P(x,t) 和流量Q(x,t) 作为基本状态量,将管道系统看成是R、L、C、G 回路,利用电传输线理论,推导出流体传输管道动态特性的基本方程,建立二输入和二输出的四端口网络基本关系式,最后写成矩阵形式
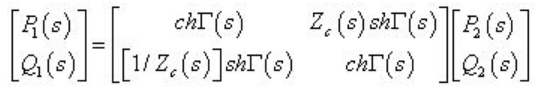
式中,Zc(s)=[Z(s)/Y(s)]1/2,而Z(s)=R Ls —串联阻抗;Y(s)=G Cs —并联导纳。以上矩阵形式中,若压力乘以管内流体截面积,流量除以管内流体截面积,则可以转化为标准的阻抗分析法。若给定输入,自然可求得系统的输出。
以上矩阵形式表示的阻抗分析法在形式上为频域传递矩阵法,特点是引入复阻抗,包括机械阻抗和声阻抗,它们是与充液管道部件的几何参数、流体与结构的物理参数有关的。对于几何形状规范的管道元件,其机械阻抗和声阻抗可以通过解析法推导出,复杂管件只能通过实验测得。
蔡的方法是有局限性的。虽然原理简单,但没有考虑管壁结构的横向运动及管壁结构与流体的耦合作用。因此,其适用范围是十分有限的。结构对流体的影响仅表现在管道内径D、管壁厚度e、管壁材料的杨氏弹性模量E 对管中流体压力波传播速度的影响,如果要分析空间管道系统的振动与声传播问题,还需要进一步研究。
此外,1992年,Singh 等利用响应谱法 (Response SpectrumMethods) 研究了多支撑空间管道系统在地震激励下的动响应。
以上的研究一般都没有考虑流体与管壁的连接耦合影响,泊松耦合也考虑不多。关于粘性流与管道的耦合振动还只停留在简单直管和曲管的状态,粘性层流与空间管系的耦合振动计算还未见有文献报导。
六、管道振动及噪声的控制技术
管道振动与噪声的控制技术分为主动控制和被动控制。这种技术是一个很热门的研究领域,已有很多论文发表。这对于直管道单一频率的振动和噪声的降噪效果是明显的,实现也不难。但对于复杂的空间管系,由于振动和噪声的复杂性与随机性,控制设备实施困难。对于潜艇或舰船中的管道系统,采用被动控制技术不会过分增大系统的体积和结构复杂性。被动控制主要有以下几种方法:
1 在管道与基础之间安装阻尼器
Budny 讨论了空间管道系统中安装阻尼器对流体瞬态压力和管道振动的影响。管道系统中常用的阻尼器有粘弹性阻尼器 (VED) 和弹塑性阻尼器 (EPD),它们可有效地抑制管道振动,降低流体脉动压力的幅值,并使其衰减速度加快。
2 管道中连接脉动压力衰减器
Shin 等对这种方法进行了理论分析与实验,结果证明这是一种降低管内压力脉动的有效方法,这种装置相当于弹簧阻尼系统。
3 采用挠性接管
挠性管接头可以减小振动在管壁内的传递,同时对声传播有抑制作用。
4 管壁选用吸振材料增加对声波的吸收
这方面已有研究,如1996年,Fang 和Lyons 等研究了管壁的材料阻尼对振动的衰减作用,在管壁的外面包一层阻尼材料降低管道系统对周围空间的声辐射。




