有限元求解:结构应力法如何实现的网格不敏感呢?
一、导读
一、悬臂梁的计算困惑
 ,根据材料力学公式,梁的中部上下表面两个点的理论解为
,根据材料力学公式,梁的中部上下表面两个点的理论解为 。
。
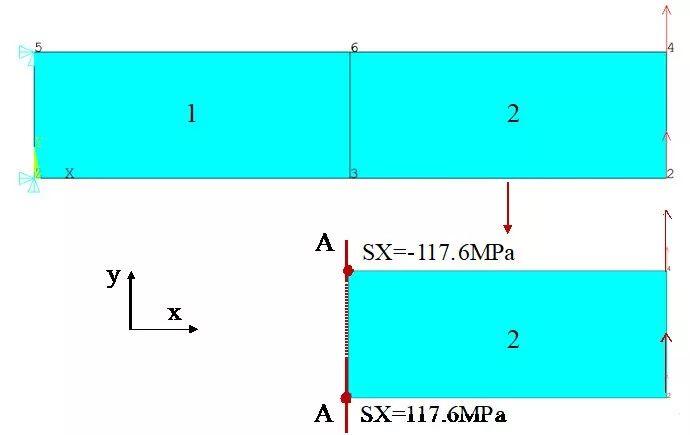
 ,这个结果与理论解相差很远,网格细化后,应力肯定会逐渐升高,感兴趣的小伙伴可以试一试到底细化到什么程度能和理论解对上。
,这个结果与理论解相差很远,网格细化后,应力肯定会逐渐升高,感兴趣的小伙伴可以试一试到底细化到什么程度能和理论解对上。三、 如何实现的网格不敏感

 (1)
(1)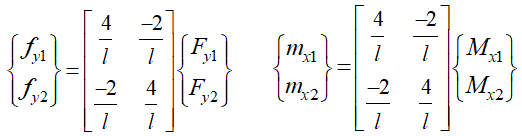 (2)
(2)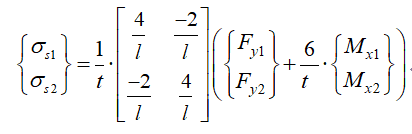 (3)
(3)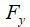 分别为
分别为 ,没有节点弯矩,如图3所示,在图3中还用箭头描述了弯曲情况下截面的应力分布。节点3和节点6的距离为
,没有节点弯矩,如图3所示,在图3中还用箭头描述了弯曲情况下截面的应力分布。节点3和节点6的距离为 ,板厚
,板厚 ,根据公式(3)的节点3和节点6的结构应力为
,根据公式(3)的节点3和节点6的结构应力为 ,这个结构应力与理论结果一致。
,这个结构应力与理论结果一致。



四、实际结构中的应用

 至
至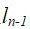 ,根据力的平衡方程,可求得各节点力
,根据力的平衡方程,可求得各节点力 与线力
与线力 的对应关系。
的对应关系。 (4)
(4)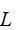 只与节点距离相关,这里定义为单元长度等效矩阵:
只与节点距离相关,这里定义为单元长度等效矩阵: (5)
(5)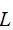 矩阵求逆,结果为
矩阵求逆,结果为 ,由于求逆后数据不再是带状,这里不详细列出,感兴趣的小伙伴试一试。
,由于求逆后数据不再是带状,这里不详细列出,感兴趣的小伙伴试一试。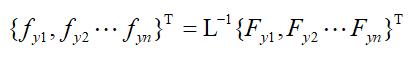 (6)
(6)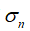 ,以及各节点力
,以及各节点力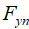 及力矩
及力矩 可用矩阵方式表为:
可用矩阵方式表为: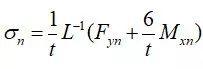 (7)
(7)五、算例分析

登录后免费查看全文
著作权归作者所有,欢迎分享,未经许可,不得转载
首次发布时间:2019-10-29
最近编辑:8月前
相关推荐
热门文章






