【JY】浅谈混凝土结构/构件性能试验指标概念(一)
【写在文前】
目前的科技水平尚不能准确预测并控制地震的发生,因为人们的目光放在了提升房屋的抗震性能上。抗震性能良好的结构应具有足够的强度和刚度来抵御地震作用,且应具有良好的能量耗散能力来消耗地震能量,更为重要的是,结构应具有足够大的延性来保证结构在屈服之后仍具有足够的强度来避免突然的破坏倒塌。因此,对结构的抗震性能展开全面的评估是非常有必要的。为什么要进行结构性能设计呢?详情请看:
【抗震性能试验分析】
目前我国常用的结构是混凝土结构。在混凝土结构、节点或构件的抗震性能试验分析中,我们一般从“定量”和“定性”两种角度来分析。
所谓“定量”,即研究对象的滞回曲线、骨架曲线,累计耗能,等效黏滞阻尼比,屈服位移,极限位移,延性系数,刚度退化等,从数据中得到研究对象的力学性能。
所谓“定性”,即研究对象的裂缝开展形态,破坏模式,塑性铰的产生等,从直观的现象中得到研究对象的受力特征。
实质上,两者是相通的,从定量性的曲线中能反映出结构的受力特征;反之,从宏观的现象中也能反映出结构的耗能能力,延性,强度等。为了解结构/构件的力学性能,目前针对于结构、节点及构件的抗震性能试验研究多采用拟静力试验。
(对于混凝土构件拟静力试验模拟分析,详情请看:)
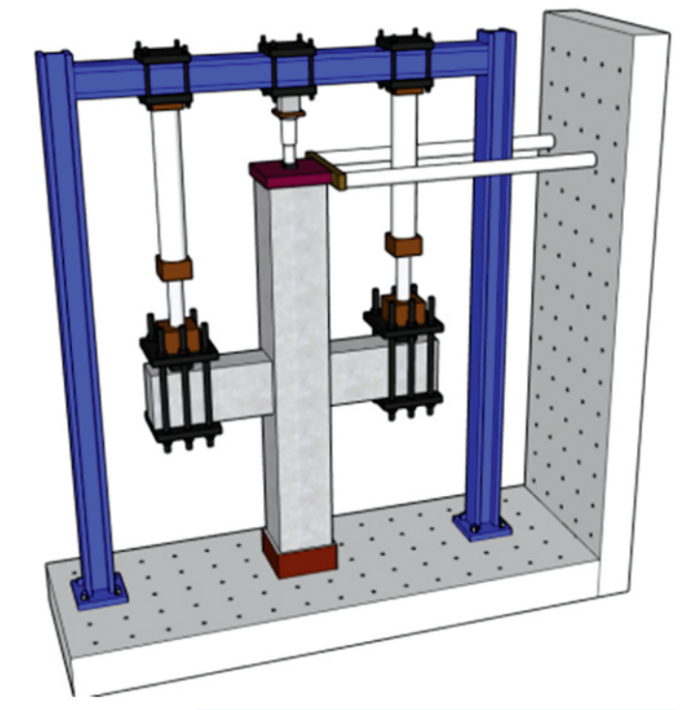
【定量指标概念】
(1)滞回曲线
滞回曲线(又称恢复力特性曲线)是恢复力随着变形变化的曲线。在结构/构件抗震试验分析中,恢复力模型是进行抗震分析的基础。滞回曲线反映结构在反复受力过程中的变形特征、刚度退化及能量消耗,是确定恢复力模型和进行非线性地震反应分析的依据。根据滞回曲线可得到结构、构件或节点的骨架曲线和耗能性能,进一步可分析变形能力、延性、刚度退化、强度退化、承载力等力学特性。
在循环荷载作用下,钢筋混凝土构件的滞回曲线一般具有以下特点:
a)混凝土受拉开裂及钢筋的受拉屈服使刚度降低;
b)屈服后,在同一级位移处,第二、三次加载的承载力和刚度均低于第一次加载(强度退化)。
根据材料、受力及构造的不同,结构、节点或构件的滞回曲线的典型形状一般有如下四种:
① 梭形
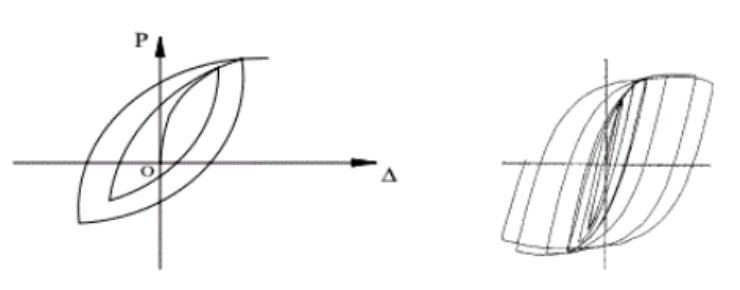
梭形说明滞回曲线的形状非常饱满,反映出整个结构或构件的塑性变形能力很强,具有很好的耗能能力。例如受弯、偏压、压弯以及不发生剪切破坏的弯剪构件,具有良好塑性变形能力的钢框架结构。
② 弓形

弓形具有一定的“捏缩”效应,显示出滞回曲线受到了 一定的滑移影响。滞回曲线的形状比较饱满,但饱满程度比梭形要低,反映出整个结构或构件的塑性变形能力比较强,能较好地吸收地震能量。例如剪跨比较大,剪力较小并配有一定箍筋的弯剪构件和压弯剪构件,一般的钢筋混凝土结构等。
③ 反S形

反S形反映了更多的滑移影响,滞回曲线的形状不饱满,说明该结构或构件延性和吸收地震能量的能力较差。例如一般框架、梁柱节点和剪力墙等。
④ Z形

Z形反映出滞回曲线受到了大量的滑移影响,具有滑移性质。例如小剪跨而斜裂缝又可以充分发展的构件以及锚固钢筋有较大滑移的构件等。
(对于理论滞回模型,可阅读:)
(2)骨架曲线
滞回曲线上同向(拉或压)各次加载的荷载极值点依次相连得到的包络曲线称为骨架曲线。骨架曲线是每次循环加载达到的水平力最大峰值的轨迹,反映了构件受力与变形的各个不同阶段及特性(强度、刚度、延性、耗能及抗倒塌能力等),也是确定恢复力模型中 特征点的重要依据。
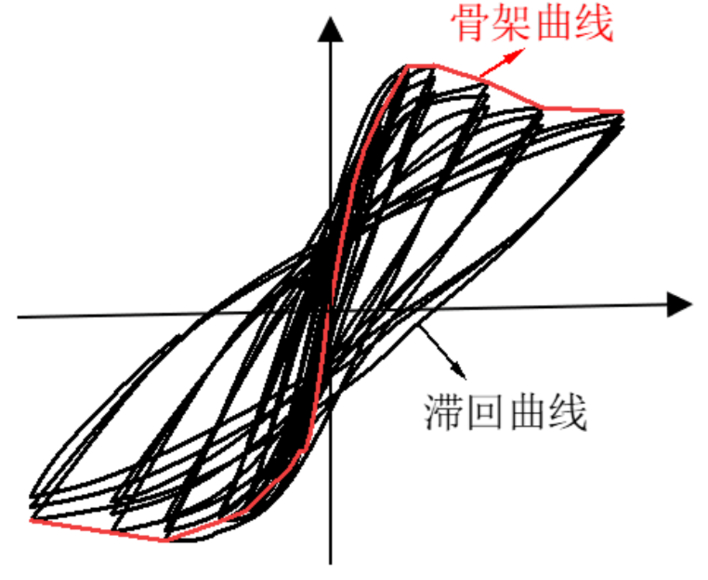
(3)耗能能力
耗能能力是结构、构件或节点在地震作用下的一项重要的抗震性能指标。引起结构耗能的原因主要有两个方面:阻尼耗能和弹塑性耗能。
(阻尼元件中也经常在消能减震结构中产生于阻尼耗能,详情可见推文:)
在此我们主要讨论结构或构件超过弹性极限后的弹塑性耗能。目前,对耗能能力常用的两项指标为累计耗能和等效黏滞阻尼比,两者具有不同的特征。累计耗能为滞回曲线的包络面积,它反映了试件在地震作用下耗散地震能量的能力。等效黏滞阻尼比为滞回曲线包络面积与其对应的弹性势能的比值,反映了滞回曲线的饱满程度,用下式确定:
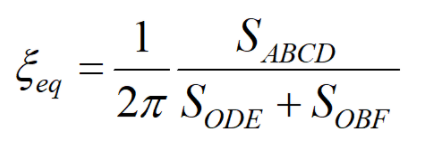
SABCD为试件滞回曲线包络面积,SODE和SOBF为在相应加载级上的正负向弹性势能。

简单来说,累积耗能为研究对象的耗能总量,等效黏滞阻尼比为研究对象的耗能效率。两者为两个不同的概念,累积耗能多的结构等效黏滞阻尼比不一定大,反之,等效黏滞阻尼比大的结构累积耗能不一定多。所以我们在做抗震试验分析时需要通过这两个指标对其耗能性能进行综合评估。
(4)延性
在钢筋混凝土结构/构件的抗震性能试验研究分析中,有四个状态是我们所关心的,分别是开裂点、屈服点、峰值点和破坏点。通常我们可以认为从结构发生屈服之后就不宜再继续使用。因此,从屈服点到最终的破坏点这一阶段,即是结构或构件的延性发展阶段。通俗来从结构自己说“我快不行了”开始,到最终说“我无了”结束,认为是其塑性变形阶段。延性好的结构,构件或构件的某个截面的后期变形能力大,在达到屈服或最大承载能力状态后仍能吸收一定量的能量,能避免脆性破坏的发生,给住户有充足的时间进行撤离。于是我们可以通过引入延性系数来定量地定义结构或构件的变形能力:

前者为位移延性系数,后者为转角延性系数,在本质上两者是一致的。由于结构或构件的极限状态难以确定,一般可简单定义为荷载下降到80% ~ 85%峰值荷载时所对应的位移。关于屈服点的确定并不唯一,因为屈服点受到轴力的影响,不同研究者可能定出不同的屈服点。目前常用的方法有以下几种:
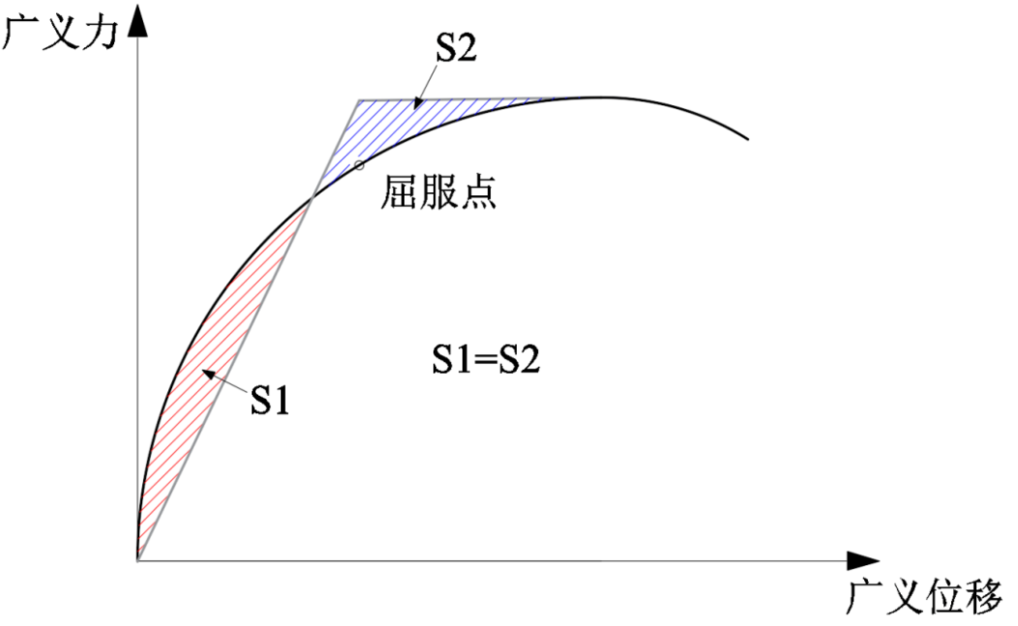
a)等能量法
该方法由Park R.在1989年提出。该方法用包络面积相等的理想弹塑性二折线代替原来的曲线,将二折线拐点的位移作为屈服位移在曲线上对应的点为屈服点。该方法不能通过作图获得屈服点,需要用数值积分试算,在操作上较为复杂,且对具有二次刚度的双线性构件将得到不合理的结果。
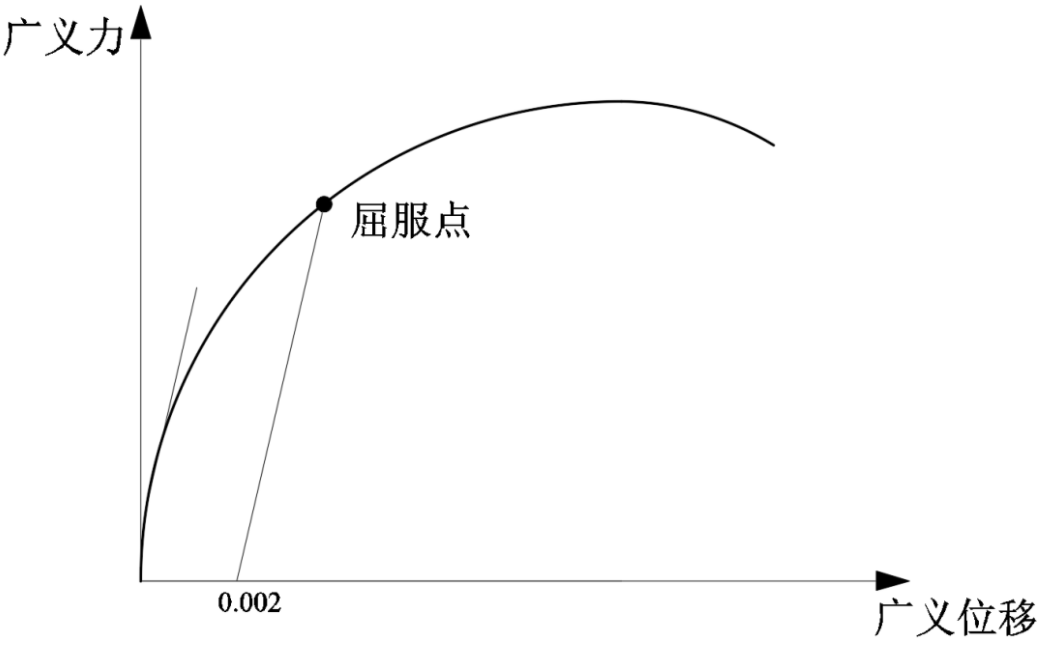
b)残余塑性变形法
该方法套用套用金属材料的规定,以塑性残余变形为0.2%确定屈服点。但直接将金属材料单轴屈服点推广到构件、结构中,会出现不合理的情况。
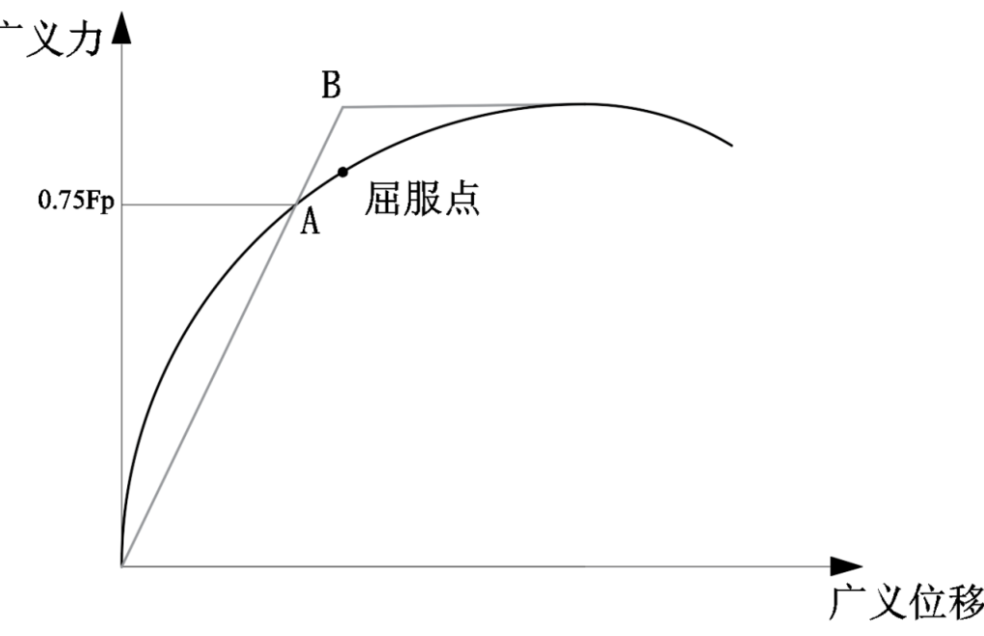
c)0.75作图法
该方法取0.75倍峰值荷载点A,作原点O与点A的连线,与峰值点水平线相交于B,将B点位移作为屈服位移,对应的点为屈服点。该方法计算较为简单,但屈服荷载系数0.75的确定具有一定的随意性。
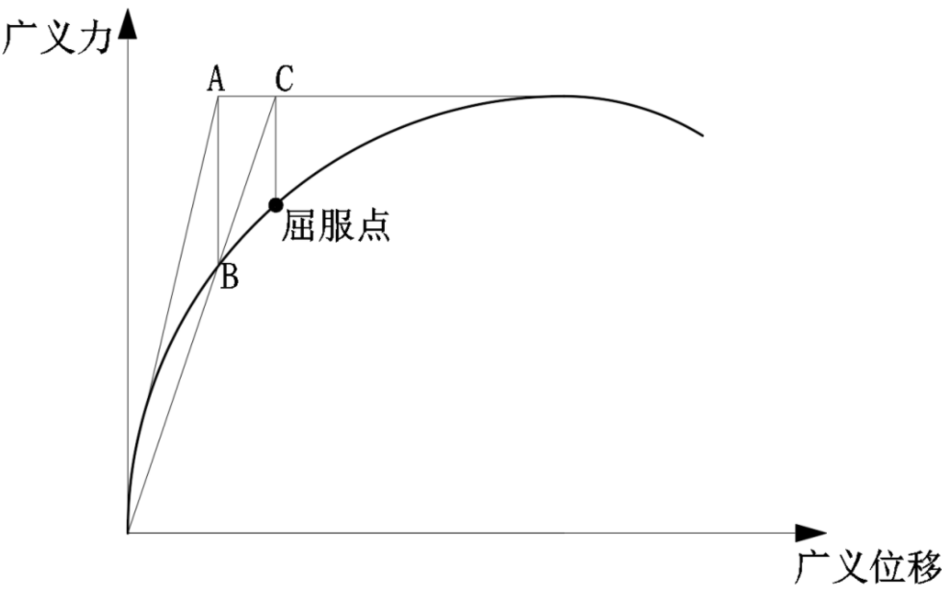
d)初始刚度作图法
该方法作直线OA与初始段相切,与过峰值点的水平线交于A点,作垂线AB与曲线交于B点,连OB并延伸与水平线交于C点,将C点的位移作为屈服位移在曲线上对应的点为屈服点。但作图过程中初始刚度的确定将对最终屈服点的确定产生较大的影响。
关于延性多大合适,并无明确规定,一般认为大于3为合理的范围,仅从提高屈服后的变形能力考虑,延性增大有利于提高结构或构件的变形性能。
对于屈服拐点不明显的试件而言,目前研究中采用的较多的是“等能量法”及“0.75作图法”。前者力学原理清晰,但操作计算较为复杂,需要采用数值积分试算;后者计算较为简单,但该方法具有一定的随意性。
(5)刚度退化
结构或构件进入塑性阶段的非线性特征,主要是刚度的改变。在循环反复荷载作用下,当保持相同的峰值荷载时,峰值点位移随循环次数的增加而增大,这种现象称为刚度退化。它反映了试件损伤的发展,是一项重要力学性能指标,常采用割线刚度表征:
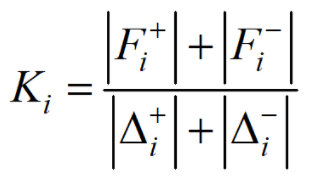
Fi 和 Fi-在某加载级上正负向峰值荷载,∆i 和 ∆i-是某加载级上正负向峰值位移。此处力和位移是广义的,当对应为荷载和位移时,所对应的刚度为侧向刚度;当对应为弯矩和转角时,所对应的刚度即为抗弯刚度。
【结语】
如果把一个结构/构件比作一个人的话,对结构/构件进行抗震性能试验的分析,就好比对一个人进行体检,体检报告的结果是这个人够不够高,肌肉够不够发达,柔韧性好不好等等。抗震性能试验能反映出结构/构件的优缺点,以及我们关心的原本力场下的各个力学性能指标,可让我们进步了解结构、构件及节点构造本身的力学性能属性。
下期再见!




